Фазовая плоскость. Бегущие волны.

В упражнениях 1 и 2 мы получали решения заданных уравнений, используя подстановку значений в готовую формулу. При этом область решения определялась автоматически по полученному графику. В этом подразделе мы рассмотрим детально поведение полученных решений из упражнений 1 и 2.

При аналитическом решении задачи предварительно всегда проводят анализ будущего решения, выявляя подобласти с определенными его свойствами. Для выявления характера решения задачи удобно воспользоваться плоскостью состояний 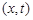или фазовой плоскостью.

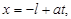
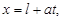
Пусть начальное отклонение струны и (или) начальный импульс локализованы в области [– l, l]. Проведем через концы отрезка локализации прямые 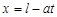. Такие прямые называют характеристиками. Получим картину, аналогичную представленной на рис.П. 2.

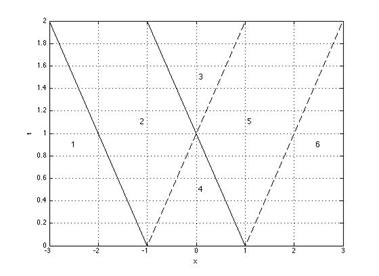
Рис.П. 2. Фазовая плоскость для случая l = 1, a = 1.

Полуплоскость t > 0 разбивается на шесть областей. Рассмотрим поведение решения в каждой из них отдельно.

Сначала рассматриваем случай нулевой начальной скорости ψ(y) = 0. Решение задачи будет представлять собой комбинацию двух бегущих волн, каждая из которых описывается функцией u = φ(x)/2. Первая волна будет «бежать» влево и ее границы будут всегда совпадать с характеристиками, изображенными пунктиром, вторая волна будет «бежать» вправо и ее границы будут совпадать с характеристиками, изображенными сплошными линиями.

В областях 1, 3 и 6 в этом случае колебаний не будет; в области 2 будет только левая волна; в области 5 только правая; в области 4 колебания будут являться суммой двух волн.

Пример П. 4.Пусть дана задача Коши для неограниченной струны:

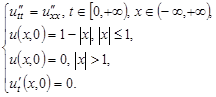
Фазовая плоскость для этой задачи совпадает с фазовой плоскостью на рис.П. 2. Построим графики решения задачи для моментов времени t = 0; t = 0.5; t = 1 и t = 1.5, воспользовавшись представлением решения в виде комбинации двух бегущих волн.

Программа для построения данных графиков будет иметь вид:

a=1;l=1;dx=0.01;

x=-4*l:dx:4*l;

% Сначала задаем значения по формуле без учета границы:

u=l-abs(x);

u(abs(x)>l)=0; % Затем просто обнуляем лишнее

u_left=0.5*u; % Левая волна

u_right=0.5*u; % Правая волна

for t=0:0.5:1.5

subplot(2,2,2*t+1);

hold on;

u1=circshift(u_left,[0 -a*t/dx]); % Сдвиг левой волны влево

u2=circshift(u_right,[0 a*t/dx]); % Сдвиг правой волны вправо

plot(x,u1,'k-'); %Левая волна (сплошная линия)

plot(x,u2,'k--'); %Правая волна (штриховая линия)

plot(x,u1+u2,'k:') %Сумма волн (пунктирная линия)

xlim([-4*l 4*l]);

ylim([0 1]);

grid on;

xlabel('x');

ylabel('u');

title(['t=' num2str(t)]);

end

Результат выполнения программы представлен на рис.П. 3.

Рис.П. 3. Графики бегущих волн

Теперь рассмотрим случай нулевого начального отклонения φ(x) = 0. В этом случае характерные области сохраняются те же, но форма решения будет описываться более сложным образом.

В областях 1 и 6, как и в первом случае, колебаний не будет.

В области 2 будет наблюдаться бегущая влево волна, форма которой в нулевой момент времени описывается уравнением

В области 5 будет наблюдаться бегущая вправо волна, форма которой в нулевой момент времени описывается уравнением

В области 3 решение будет задано константой, равной значению интеграла

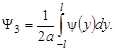
Значение интеграла в области 3 совпадает со значениями на границе областей 2 и 5. Наиболее сложная форма решения в области 4. В зависимости от x она описывается уравнением:

В общем случае, когда и начальное отклонение и начальная скорость не равны нулю, решение описывают как комбинацию двух решений: первое – это комбинация двух бегущих волн, созданных начальным отклонением, второе – это решение, зависящее только от начальной скорости.

Упражнение П.4.Дана задача Коши для неограниченной струны:

Построить фазовую плоскость для данной задачи и графики решения для моментов времени 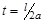, , 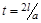. Для построения воспользоваться построенной фазовой плоскостью и представлением в виде бегущих волн для характерных областей.

Оглавление

Предисловие………………………………………………………………3

Глава 1. Дифференциальные уравнения в частных производных, их классификация и методы решения. Задача Коши………………5

1.1. Дифференциальные уравнения в частных производных

1.1.1. Дифференциальные уравнения в частных производных второго порядка……………………………………. 6

1.1.2. Понятие об общем решении уравнения в частных производных……………………………………………………. 8

1.2. Начальные и граничные условия……………………... 11

1.2.1. Задача Коши для дифференциальных уравнений первого порядка……………………………………………… 11

1.2.2. Задача Коши для дифференциальных уравнений второго порядка ……………………………………………..12

1.3. Классификация уравнений второго порядка в частных производных………………………………………………….. 14

1.4. Численные методы решения дифференциальных уравнений в частных производных…………………………………. 15

1.4.1. Использование метода сеток для решения параболических уравнений в частных производных………….. 15

1.4.2. Использование метода сеток для решения гиперболических уравнений в частных производных………. 20

1.4.3. Использование метода сеток для решения эллиптических уравнений в частных производных………… 23

Глава 2. Уравнение колебания струны……………………………. 27

2.1. Вывод уравнения колебания струны………………….. 27

2.2. Методы решения уравнения колебания струны……… 31

2.2.1. Метод Даламбера (метод бегущих волн) для бесконечной струны………………………………………………… 31

2.2.2. Фазовая плоскость………………………………….. 35

2.2.3. Метод продолжения для полубесконечной струны ………………………………………………………………..41

2.2.4. Метод продолжения для конечной струны (начальная и конечная точка жестко закреплены)…….. 44

2.3. Метод Фурье (метод стоячих волн) или метод разделения переменных……………………………………………... 55

Глава 3. Уравнения теплопроводности и Лапласа………………. 67

3.1. Вывод уравнения теплопроводности………………….. 67

3.2. Метод Фурье для конечного стержня…………………. 68

3.3. Уравнение Лапласа……………………………………….. 73

3.3.1. Задача Дирихле для уравнения Лапласа в круге… 73

3.3.2. Задача Дирихле для уравнения Лапласа в кольце.. 77

3.3.3. Задача Дирихле для уравнения Лапласа в прямоугольнике………………………………………………………... 79

Рекомендуемая литература……………………………………………. 83

Индивидуальные задания……………………………………………. 84

Приложения. Практикум в среде MATLAB………………………… 89

Учебное издание

Асоцкий Данил Иванович

Борзистая Екатерина Леонидовна