
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Одномерная оптимизация. Необходимые и достаточные условия оптимальности. Принцип сужения интервала неопределенности для унимодальных функций.
Математическая постановка задач оптимизации. Критерии оптимизации. Виды ограничений. Классификация задач: задачи безусловной и условной оптимизации, одномерной и многомерной оптимизации, задачи нелинейного, линейного, целочисленного программирования, задачи оптимизации на сетях.
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например: - количество продукции - "расход сырья" – кол-во продукции - "качество продукции" Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
Постановка задачи
Пусть функция f(x) - унимодальная, по крайней мере, на отрезке [a,b] и известны ее значения на концах этого отрезка. Т.е. минимум локализован и необходимо определить его как можно точнее, с наименьшим возможным интервалом неопределенности, но при этом возможно выполнить только n вычислений функции? Как следует выбрать n точек xk, k=1,..,N вычисления функции на отрезке [a,b], чтобы как можно точнее определить минимум?
Виды ограничений
Несмотря на то, что прикладные задачи относятся к совершенно разным областям, они имеют общую форму. Все эти задачи можно классифицировать как задачи min-ции вещественнозначной функции f(x) N-мерного векторного аргумента x=(x1, x2,..., xn), компоненты которого удовлетворяют системе уравнений hk(x)=0, набору неравенств gi(x) 0, а также ограничены сверху и снизу, т.е. xi(u) xi xi(l). В последующем изложении функцию f(x) будем называть целевой функцией, уравнения hk(x) =0 - ограничениями в виде равенств, а неравенства gi(x) 0 - ограничениями в виде неравенств. При этом предполагается, что все фигурирующие в задаче функции являются вещественнозначными, а число ограничений конечно.
Классификация задач
Задачи оптимизации можно классифицировать в соответствии с видом функций f, hk, gi и размерностью вектора x. Задачи без ограничений, в которых x представляет собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но вместе с тем весьма важный подкласс оптимизационных задач. Задачи условной оптимизации, в которых функции hk, и gi являются линейными, носят название задач с линейными ограничениями.
В таких задачах целевые функции могут быть либо линейными, либо нелинейными. Задачи, которые содержат только линейные функции вектора непрерывных переменных x, называются задачами линейного программирования; в задачах целочисленного программирования компоненты вектора x должны принимать только целые значения.
С точки зрения методологии изложения методов минимизации функций целесообразно выделить такие задачи.
1.Безусловная минимизация функций:
В этом случае область задания функции Q - все n-мерное евклидово пространство, т. е. на переменные функции ограничений не накладывается вообще. Очевидно, что минимум функции (если он существует) всегда находится внутри ее области задания, поскольку последняя просто не имеет границ.
2.Минимизация функций при ограничениях в виде равенств:
у(х)
W : fi(х)=0 (i=1, ... , m; m<n)
Область задания W функции- бесконечное множество решений системы уравнений, представляющее собой p-мерную поверхность в n-мерном пространстве. Поскольку любая точка х  W лежит на поверхности fi (х) == 0 (i = 1, ... , m) и, следовательно, является граничной, то и минимум (в случае его существования) также лежит на границе области W.
W лежит на поверхности fi (х) == 0 (i = 1, ... , m) и, следовательно, является граничной, то и минимум (в случае его существования) также лежит на границе области W.
3.Минимизация функций, заданных на гиперпараллелепипеде:
у(х)
W : fi(х) =0 (i=m+1,... , m+k)
fi(х) = 0 (i=1, ..., m).
Здесь минимум функции может находиться внутри области и на ее границах
4.Минимизация функций при ограничениях в виде неравенств.
у(х)
W : fi(х) 0 (i=1, :. , k)
х 0
Минимум может находиться внутри области W и на ее границе.
Задачи 1, 2 обычно относят к классическим задачам оптимизации; 3, 4 называют задачами математического программирования. Легко видеть, что задачи 1-3-частный вырожденный случай задачи 4.
Одномерная оптимизация. Постановка задачи. Метод квадратической аппроксимации.
Постановка задачи:Пусть функция f(x) - унимодальная, по крайней мере, на отрезке [a,b] и известны ее значения на концах этого отрезка. Т.е. минимум локализован и необходимо определить его как можно точнее, с наименьшим возможным интервалом неопределенности, но при этом возможно выполнить только n вычислений функции? Как следует выбрать n точек xk, k=1,..,N вычисления функции на отрезке [a,b], чтобы как можно точнее определить минимум?
Постановка задачи безусловной оптимизации ФНП. Методы нулевого порядка. Метод покоординатного спуска.
Постановка задачи:
Дана непрерывно дифференцируемая функция F(x1,x2,...,xn) n переменных. Необходимо найти хотя бы одну точку локального оптимума этой функции:
F(x) ---> opt ,где x = (x1,x2,...,xn).
Методы нулевого порядка.
В случае, когда свойства оптимизируемой функции неизвестны или она не является дифференцируемой во всей области поиска, то исследователь вынужден использовать методы нулевого порядка, опирающиеся только на значения функции.
Перед непосредственным применением методов прямого поиска необходимо провести ряд мероприятий по подготовке задачи к решению, а именно
· исключить ограничения в виде равенств;
· определить начальную допустимую точку.
Простейший способ исключения ограничений в виде равенств заключается в решении его относительно одной из переменных с последующим исключением этой переменной путем подстановки полученного выражения в соотношения, описывающие задачу. При этом следует учитывать, что границы значений исключаемых переменных сохраняются в задаче в виде ограничений - неравенств.
Для определения начальной допустимой точки целесообразно использовать процедуру случайного поиска, основная идея которого будет рассмотрена ниже.
После проведения процедуры подготовки задачи к решению следует приметить один из методов условной оптимизации. Рассмотрим методы прямого поиска:
1.2& Метод покоординатного спуска.
Основан на поочередной оптимизации вдоль каждой из координатных осей.
АЛГОРИТМ ПОКООРДИНАТНОГО СПУСКА.
1. Выбор x0 (начального приближения), epsg и epsx (точности решения по градиенту и аргументу).
2. iter:= 0; h= 0,1*epsx. (инициализация счетчика итераций и пробного шага)
3. j=1.
4. x=x0, f0=f(x0)
5. xj= x0j+h; Dx=x-x0
6. Расчет значения функции f(x).
7. Если f(xj)< f0, то p=+Dx, иначе p=-Dx. (направление поиска)
8. Выбор длины шага s=a*p (a>0) вдоль выбранного направления p.
9. x0:= x0 + s; j=j+1;
10. Если j<n, то идти к п.4.
11. iter:=iter+1.
12. Если |s|> epsx (точность по аргументу), то идти к п.3.
13. Печать вектора x0, значения оптимизируемой функции f(x0) и количества итераций iter.
Метод Монтер-Карло
Суть: задаем начальную точку и куб с n количеством разбросанных точек, если х1 лучше х0, то рис следующий квадрат и разбрасываем снова точки и ищем наилучшую,если ее нет то уменьшаем область R(квадрата) и т д
Алгоритм:
1. Ввод начальной точки х0, размера R, количество точек N, которые бросаем, точность Ех, Еf
2. Вокруг начальной точки разбрасываем N точек в куб размером R.
For i=1,N, теперь для каждой точки, рассчитываем случайное отклонение от х0
For j=1,n, где n- размерность задачи.
Δj= - R/2+rnd R, где rnd – число в интервале [0,1]
x <i> =x0+Δ сгенерировали точки
3.Расчитываем  , при i=1,N
, при i=1,N
4. Ищем х-мин. fmin=f(xmin), xmin= ?
5. Локализуем удачность шага, если fmin<f(x0), то шаг удачен x0=xmin, иначе шаг не удачен, то уменьшаем R=R/2
6. если не удовлетворяется условие Ех, то идем к п.2
7.выводим х0, f(x0), R, Δf
Критерии останова сходимости метода:
1)R<Ex
2) Δf<Ef, где Δf-значение получившейся функции f n-1 – f n
Δf=f n-1 – f n >0
3) Δf/ Δr <Eg
Метод наискорейшего спуска
Самый известный из семейства градиентных методов это метод наискорейшего спуска. Он так назван потому, что спуск вдоль антиградиентного направления осуществляется в точку минимума.
Алгоритм:
1.вводим x0 (начального приближения), eg-точность по градиенту конечного решения и e1g точность по производной по направлению).
2.Пока /f ’(x0)/<eg, n=0
2.1.вычисляем направление спуска Pk= - f ’(x0)= - grad (x0), при к=к+1
2.2 Производим одномерную оптимизацию поиска из точки х0 вдоль направления Рк, то х1=argmin f(x0+αPk) c точностью e1g (e1g≤eg)
2.3 Критерии останова
Δх=х1-х0, если /Δx/<ex, то аварийный выход, застряли х0, f(x0), f ’(x0), /Δx/-длина последнего шага
2.4х0=х1
3. вывод полученного значения х0, f(x0), f ’(x0)
Метод Ньютона.
Метод Ньютона основан на линейном приближении вектор-функции g(x)=(g1(x),g2(x),...,gn(x)), а именно:
g(x) ≈ g(x0 ) + G(x0 )*(x - x0 ) ,
где  - матрица первых производных функции g(x) , она же матрица Гессе (матрица вторых производных) для оптимизируемой функции f(x).
- матрица первых производных функции g(x) , она же матрица Гессе (матрица вторых производных) для оптимизируемой функции f(x).
Т.к. необходимо найти x*, для которого g(x*)= 0, то, подставляя ноль в левую часть равенства (3), получим формулы для приближения корня системы уравнений (2):
G(x0)*Dx = - g(x0), x = x0 + Dx
В дальнейшем вектор приращения или направление поиска Dx будем обозначать буквой р.
Алгоритм:
1. Выбор x0 (начального приближения), eg и ex (точности решения по градиенту и аргументу).
2. k:= 0. (инициализация счетчика итераций)
3. Аналитическое определение всех частных производных функции f(x) - gj(x), т.е. вектора градиента и G(x) - матрицы вторых производных - для оптимизируемой функции.
4. Расчет g(x0).
5. Расчет G(x0).
6. Решение системы (4), например, методом Гаусса или методом Зейделя, т.е. определение р=Dx - шага.
7. x:= x0 + р ; k:=k+1.
8. расчет g(x).
9. Если |р|< ex (точность по аргументу) или |g(x)|< eg , то идти к п.11.
10. x0:= x ; g(x0):=g(x); идти к п.5.
11. Оценка погрешностей измерения значения функции df и определения оптимума dx.
12. Выводим вектор x и g(x) , значения оптимизируемой функции f(x) и количества итераций к.
Графическое решение ЗЛП. Основные понятия и идея решения задачи.
Если число неизвестных в задаче линейного программирования равно двум, т.е. n = 2, то ее можно решить графическим методом. Кроме того, графический метод дает геометрическую интерпретацию решения ЗЛП.
Пример:
Задача: Предприятие производит краски 2-х видов: I – для внутренних работ, E – для внешних работ. A,B – исходные продукты, использующиеся для производства I,E.
Доход от реализации 1т краски I – 2000$, E – 3000$
Коэффициенты расхода исходных продуктов A и B на производство 1т краски I и E:
| I | E | Суточный запас, тонн | |
| A | |||
| B |
Известно, что суточная потребность краски для внутренних работ не превышает 2т, т.е. суточный спрос на I <=2т. Суточный спрос I не превышает суточного спроса на E больше чем на 1т.
Найти: оптимальный суточный план производства красок, максимизирующий ожидаемый максимальный доход.
Математическая постановка задачи:
Обозначим XI(т/сут) – краски I ; XE(т/сут) – краски E.
Целевая функция: 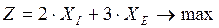 - ожидаемый максимальный доход
- ожидаемый максимальный доход
Ограничения на запас продукта А: 
Ограничения на запас продукта В: 
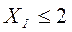 ,
,  ,
, 
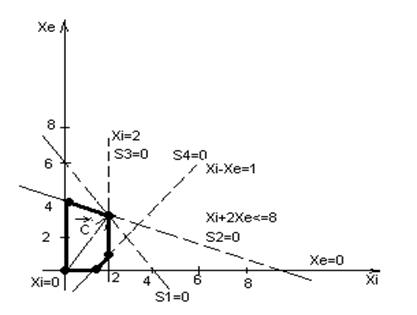
При XI=0 и XE=0 
Найдем точку пересечения:

-3XI=-4 XI=4/3 XE=10/3
Z(4/3;10/3)=38/3 Z(0;4)=12
Идея решения задачи: Используя Симплекс-метод, получить последовательность базисных решений и оптимальное решение.
Целевая функция представляет собой взвешенную линейную сумму от неизвестных переменных xi вида: Z=c*xi c- вектор целевой функции.
Ограничения, накладываемые на область возможных решений, имеют вид линейных равенств или неравенств: 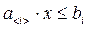 где ai, bi - известные величины, причем величины aj, xi, bi положительные.
где ai, bi - известные величины, причем величины aj, xi, bi положительные.
Допустимым решением задачи линейного программирования будем называть любую совокупность переменных
х1³ 0, х2³ 0, ¼ , хn ³0, (3.10)
удовлетворяющих уравнениям

Оптимальным решением  будем называть то из допустимых решений, для которого линейная форма Z обращается в максимум (минимум).
будем называть то из допустимых решений, для которого линейная форма Z обращается в максимум (минимум).
Выбор начального решения
Для задачи, представленной в стандартной форме, количество переменных обычно больше, чем количество ограничений. Поэтому для нахождения начального решения задачи требуется выразить m переменных (т.е. количество переменных, равное количеству уравнений) через остальные n-m переменных, принять эти n-m переменных равными нулю и, таким образом, найти значения m переменных. Переменные, значения которых принимаются равными нулю, называются небазисными, а остальные m переменных - базисными. Значения базисных переменных неотрицательны (некоторые из них могут оказаться равными нулю). Количество базисных переменных всегда равно количеству ограничений. Найденное таким образом решение называется начальным допустимым базисным решением. Оно соответствует всем ограничениям.
Начальное решение проще всего найти в случае, когда в каждом ограничении есть переменная, которая входит в него с коэффициентом 1 и при этом отсутствует в других ограничениях. Такие переменные принимаются в качестве базисных (они образуют начальный базис задачи). Остальные (небазисные) переменные принимаются равными нулю. Таким образом, базисные переменные принимают значения, равные правым частям ограничений.
Анализ ресурсов.
Предположим, что для некоторых значений А, b и с найден оптимальный план х*, максимизирующий суммарный доход 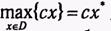 . Достаточно естественным представляется вопрос: как будет изменяться оптимальный план х* при изменении компонент вектора ограничений b и, в частности, при каких вариациях bоптимальный план х* останется неизменным? Данная задача получила название проблемы устойчивости оптимального плана. Очевидно, что исследование устойчивости х* имеет и непосредственное практическое значение, так как в реальном производстве объемы доступных ресурсов bi могут существенно колебаться после принятия планового решения х* .
. Достаточно естественным представляется вопрос: как будет изменяться оптимальный план х* при изменении компонент вектора ограничений b и, в частности, при каких вариациях bоптимальный план х* останется неизменным? Данная задача получила название проблемы устойчивости оптимального плана. Очевидно, что исследование устойчивости х* имеет и непосредственное практическое значение, так как в реальном производстве объемы доступных ресурсов bi могут существенно колебаться после принятия планового решения х* .
Когда вектор ограничений bизменяется на ∆bили, как еще говорят, получает приращение ∆b, то возникают соответствующие вариации для оптимального плана  и значения целевой функции
и значения целевой функции  . Допустим, приращение ∆b таково, что оно не приводит к изменению оптимального базиса задачи, т. е.
. Допустим, приращение ∆b таково, что оно не приводит к изменению оптимального базиса задачи, т. е.  . Определим функцию F(b), возвращающую оптимальное значение целевой функции задачи
. Определим функцию F(b), возвращающую оптимальное значение целевой функции задачи  для различных значений вектора ограничений b
для различных значений вектора ограничений b  (1.55)
(1.55)
Рассмотрим отношение ее приращения 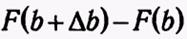 к при-
к при-
ращению аргумента ∆b. Если для некоторого i устремить 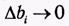 , то мы получим
, то мы получим  (1.56)
(1.56)
Учитывая, что в соответствии с теоремой 1.5  (1.57) и подставив (1.57) в (1.56), приходим к выражению
(1.57) и подставив (1.57) в (1.56), приходим к выражению 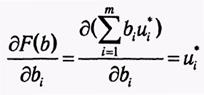 (1.58)Из формулы (1.58) вытекает экономическая интерпретация оптимальных переменных двойственной задачи. Каждый элемент ui* может рассматриваться как предельная (мгновенная) оценка вклада г-го ресурса в суммарный доход F при оптимальном решении х*. Грубо говоря, величина и* равна приросту дохода, возникающему при увеличении ресурса i на единицу при условии оптимального использования ресурсов.
(1.58)Из формулы (1.58) вытекает экономическая интерпретация оптимальных переменных двойственной задачи. Каждый элемент ui* может рассматриваться как предельная (мгновенная) оценка вклада г-го ресурса в суммарный доход F при оптимальном решении х*. Грубо говоря, величина и* равна приросту дохода, возникающему при увеличении ресурса i на единицу при условии оптимального использования ресурсов.
В различных источниках компоненты оптимального плана двойственной задачи также называются двойственными оценками или теневыми ценами, а Л. В. Канторович предлагал такой термин, как объективно обусловленные оценки.
На основе теорем двойственности для пары задач ЛП в общей формемогут быть сформулированы некоторые важные (с точки зрения экономической интерпретации) следствия.
Если при использовании оптимального плана прямой задачи i-e ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю, т. е. если 
В рамках рассматриваемой задачи производственного планирования это означает, что если некоторый ресурс bi имеется в избыточном количестве (не используется полностью при реализации оптимального плана), то i-e ограничение становится несущественным и оценка такого ресурса равна 0.
Если при использовании оптимального плана двойственной задачи j-e ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю, т. е. если 
Учитывая экономическое содержание двойственных оценок  , выражение
, выражение  может быть интерпретировано как удельные затраты на j-й технологический процесс. Следовательно, если эти затраты превышают прибыль от реализации единицы j-го продукта, то производство j-го продукта является нерентабельным и не должно присутствовать в оптимальном производственном плане (х* = 0).
может быть интерпретировано как удельные затраты на j-й технологический процесс. Следовательно, если эти затраты превышают прибыль от реализации единицы j-го продукта, то производство j-го продукта является нерентабельным и не должно присутствовать в оптимальном производственном плане (х* = 0).
Анализ цен
С точки зрения экономической интерпретации задача исследования параметрической устойчивости может быть рассмотрена как изучение тех пределов колебания цен на продукцию управляемого предприятия (фирмы), при которых принятый план выпуска продукции продолжает оставаться оптимальным.
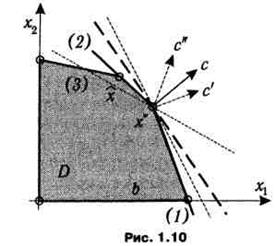 Также содержание проблемы устойчивости оптимального плана ЗЛП по отношению к вариациям целевой функции может быть проиллюстрировано с помощью первой геометрической интерпретации. На рис. 1.10 изображено множество допустимых планов D некоторой задачи ЛП. Как видно из рисунка, целевая функция f (ее поведение отражает линия уровня, показанная жирным пунктиром) достигает экстремального значения в точке х , а изменению ее коэффициентов от с к с' или с" на рисунке соответствует поворот линии уровня относительно х'. Активным, т. е. обращающимся в равенство, ограничениям в точке х соответствуют линии (1) и (2). До тех пор, пока при повороте, вызванном изменением вектора с, линия уровня целевой функции не выходит за пределы образуемого линиями ограничений конуса, х остается оптимальным планом. Как показано на рис. 1.10, этот план не меняется при переходе от с к с', и, наоборот, при переходе от с к с" линия уровня целевой функции f(x) = c"x пересечет линию (2), что вызовет изменение оптимального базисного плана, которым теперь станет точка х
Также содержание проблемы устойчивости оптимального плана ЗЛП по отношению к вариациям целевой функции может быть проиллюстрировано с помощью первой геометрической интерпретации. На рис. 1.10 изображено множество допустимых планов D некоторой задачи ЛП. Как видно из рисунка, целевая функция f (ее поведение отражает линия уровня, показанная жирным пунктиром) достигает экстремального значения в точке х , а изменению ее коэффициентов от с к с' или с" на рисунке соответствует поворот линии уровня относительно х'. Активным, т. е. обращающимся в равенство, ограничениям в точке х соответствуют линии (1) и (2). До тех пор, пока при повороте, вызванном изменением вектора с, линия уровня целевой функции не выходит за пределы образуемого линиями ограничений конуса, х остается оптимальным планом. Как показано на рис. 1.10, этот план не меняется при переходе от с к с', и, наоборот, при переходе от с к с" линия уровня целевой функции f(x) = c"x пересечет линию (2), что вызовет изменение оптимального базисного плана, которым теперь станет точка х
Целочисленное деление.
Задачи оптимизации, в которых искомые переменные должны быть целочисленными, называются задачами целочисленного программирования. В том случае, когда ограничения и целевая функция представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования.
При графическом решении задач целочисленного программирования требование целочисленности отражается в том, что решением задачи могут быть только точки, находящиеся на пересечении целочисленных значений.
Проблемы:
- округление оптимальных значений переменных в непрерывном решении может привести к недопустимому решению;
- оптимальным решением целочисленной задачи может оказаться такое решение, в котором значения переменных не являются ближайшими к оптимальному решению непрерывной задачи.
Метод ветвей и границ
В основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества (стратегия “разделяй и властвуй”). На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет. Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве. Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено. Проверяемое подмножество может быть отброшено еще и в том случае, когда в нем удается найти наилучшее решение. Если значение целевой функции на найденном решении меньше рекорда, то происходит смена рекорда. По окончанию работы алгоритма рекорд является результатом его работы.
Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т.д.
Вычисление нижней границы является важнейшим элементом данной схемы. Для простейшей задачи размещения один из способов ее построения состоит в следующем.
Метод потенциалов.
Пусть имеются 3 поставщика и 4 потребителя.


| 
| 
| 
|
 U, V – потенциалы.
U, V – потенциалы.
1)Сбалансируем задачу:
2)Определить начальн. допустимый план:

 = 9·200+4·150+6·50+3·250+5·150+3·100+3·100=4800 руб.
= 9·200+4·150+6·50+3·250+5·150+3·100+3·100=4800 руб.
3)Определение включаемой в базис переменной.
Определение потенциалов:
Ui, i=1..n; Vj, j=1..m
Базисные переменные:

Для базисных переменных: Ui+Vj=Cij (стоимость перевозки):
U1+V2=9; U2+V1=4; U2+V2=6; U2+V3=3; U2+V4=4;U3+V1=3;
U4+V4=3.
7 уравнений и 8 неизвестных => 1 переменная свободная, принимаем ее = 0.
Н-р: U1=0 => U2=-3; U3=-4; U4=-5; V1=7; V2=9; V3=6; V4=8.
Коэффициенты целевой функции (для Симплекс метода):
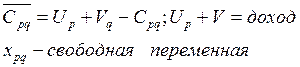

| 
|
Включ. в базис переменная X11.
4)Определение исключаемой из базиса переменной.
Построение цикла


5)Определение потенциалов:

| 
| 
| 
|

| 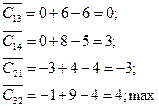
| 
|
Включаем в базис переменную С32.
 Исключаем переменную X12 (=0).
Исключаем переменную X12 (=0).

32. Задача о построении минимального покрытия графа (остова)
ПЗ: Имеется сеть из N узлов. Соединение между узлами оценивается в единицах (н-р, расстояние в м, км, ст. в руб.).
Необходимо найти такое минимальное покрытие (соед. узлов), кот. обеспечивает наличие пути (неориентированный граф) из любого узла в любой другой.


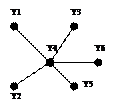

 Общая протяженность д.б. минимальной. Остовы:
Общая протяженность д.б. минимальной. Остовы:
Метод решения: Метод определения минимального остова::
1. Выбираем самое минимальное соед., заносим соед-ые узлы в список:
P Сп1={(3,4)}; список1={3,4};
2. Пока не все вершины находятся в списке: 2.1
2.1 Определим узел, не принадлежащий списку, из которого имеется самое мин. сиз которого имеется самое мин. ащий списку2.1
до множества узлов, принадлежащих списку. Добавляем это соед. в остов
P Cп2={(3,4);(2,4)} Cп2={3,4,2}
P Cп3={(3,4);(2,4);(2,5)} Сп3 = {3,4,2,5}
P Cп3={(3,4);(2,4);(2,5);(1,3)} Сп4={3,4,2,5,1}
P Cп5={(3,4);(2,4);(2,5);(1,3),(3,6)} Сп5= {3,4,2,5,1,6} P Cп – список ребер!
33.Задача о минимальном пути. Метод потенциалов
Дано:
N узлов сети и дана матрица расстояний (стоимости) соед. между уздами. Требуется найти путь минимальной длины из узла № N1 до узла № N2. Граф может быть ориентированным N1=Y1 N2=Y8

| 01 | 61 | 71 | 81 | 01 | 01 | 01 | 01 | |
| 61 | 01 | |||||||
| 71 | 01 | |||||||
| 81 | 01 | |||||||
| 01 | 01 | |||||||
| 01 | 01 | |||||||
| 01 | 01 | |||||||
| 01 | 01 |
Метод потенциалов:
Начальной вершине присваиваем 0-ой потенциал. Потенциал – минимальное расстояние между вершиной, имеющей потенциал, и другой вершиной.
1.Определение потенциала начального узла φ1=0, Сп ={1}, Edgesij=0, i,j=1..n – это ребра
2. Расчет потенциалов:
2.1. Для каждой вершины k из списка рассмотрим ребра вида Edgeskj=0, Если φj > φk +Ckj то φj = φk +Ckj , Edgeskj=0, Сп = Сп +{j}
2.2. Если существует i, j такое что Edgesij=0, то возврат к п. 2.1.
3. Определение минимального пути. Путь = (N2)
3.1. Для первой вершины имеющегося пути, k ищем j: Cjk = φk - φj
3.2. Добавляем путь Путь = Путь +{j}
3.3. Если j ≠ N1 то идти к п. 3.1
4. Вывод пути и его стоимости
Пример:
1). Сп={1}, Edgesij=0, φ1=0
2). φ2=6, φ3=7, φ4=8. Сп={1,2,3,4}
3). φ5=13, φ3=16, φ3=10 (т.к. φ3:10>7, то оставляем 7), φ6=15, φ7=17, φ7=15
4). Сп = {1,2,3,4,5,6,7}, φ8=19.
φ:
5. Нахождение оптимального пути:
Путь1=(Y5,Y8)
Путь2=(Y2,Y5,Y8)
Путь3=(Y1,Y2,Y5,Y8)
Алгоритм Форда-Фалкерсона
Впервые был предложен в 1956г. До этого времени задача решалась с помощью методов линейного программирования, что было крайне не эффективно. Алгоритм является псевдополиномиальным и имеет оценку O(nm log U), где m = |E|, n = |V|, U = max(Cij).
Алгоритм начинает свою работу с нулевого потока и на каждой своей итерации увеличивает поток в сети. На каждом шаге находится увеличивающая величину потока цепь. Поток увеличивается вдоль дуг этой цепи, пока она не станет насыщенной.
Увеличивающей цепью является цепь из источника в сток, все дуги которой допустимы. Дугу из вершины a в вершину b назовем допустимой, если выполняется одно из следующих условий:
1. f(e) < c(e) и дуга согласованна
2. f(e) > 0 и дуга несогласованна
По увеличивающей цепи можно пустить поток величины Q, где Q = min{q(ei), 1 ≤ i ≤ l} и q(e) = {с(e) – f(e), если дуга согласованна, f(e), если дуга не согласованна}. Для того, чтобы увеличить величину потока сети на Q, необходимо увеличить на Q поток на каждой согласованной дуге цепи и уменьшить на каждой несогласованной.
В своей работе [3] Форд и Фалкерсон (Ford and Fulkerson) доказали, что поток в сети, для которой нельзя построить увеличивающую цепь, является максимальным.
Для нахождения увеличивающей цепи ими был предложен “Метод расстановки пометок”. Процесс расстановки меток начинается в источнике сети и заканчивается в ее стоке. Как только сток оказался помеченным, мы можем говорить о существовании увеличивающей цепи из источника в сток. Метка, “наносимая” на вершины сети, содержит необходимый минимум информации, достаточный для того, чтобы восстановить эту цепь и определить величину, на которую можно изменить поток в ней. Вершина сети может находиться в одном из 3-х состояний: “непомеченная”, “помеченная” и “просмотренная”.
Этап 1. Расстановка меток.
Все вершины получают статус непомеченных.
Процедура расстановки меток.
Возьмем произвольный помеченный, но не просмотренный узел x. Пусть он имеет пометку [i, +, e(x)], где i – вершина из которой был помечен x;  флаг, показывающий, что дуга (i,x) согласованна; e – величина потока, который можно пропустить по этой дуге. Рассмотрим все непомеченные смежные вершины y, такие что дуга (x, y) согласованна. Пометим вершину y меткой [x, +, e(y)], где e(y) = min{e(x) , c(x, y) – f(x, y)}. Затем рассмотрим все непомеченные смежные вершины y, соединенные с ней несогласованной дугой. Пометим их меткой [x, -, e(y)], где e(y) = min{e(x), f(y,x)}. Теперь все рассмотренные узлы y имеют статус помеченных, а узел x - просмотренный.
флаг, показывающий, что дуга (i,x) согласованна; e – величина потока, который можно пропустить по этой дуге. Рассмотрим все непомеченные смежные вершины y, такие что дуга (x, y) согласованна. Пометим вершину y меткой [x, +, e(y)], где e(y) = min{e(x) , c(x, y) – f(x, y)}. Затем рассмотрим все непомеченные смежные вершины y, соединенные с ней несогласованной дугой. Пометим их меткой [x, -, e(y)], где e(y) = min{e(x), f(y,x)}. Теперь все рассмотренные узлы y имеют статус помеченных, а узел x - просмотренный.
Эта общая для всех узлов сети процедура. Пометим источник меткой [~, ~, ∞] и будем последовательно вызывать ее для всех смежных узлов, постепенно двигаясь по сети. Как только процедура будет вызвана для стока, будет получена увеличивающая цепь и следует перейти ко второму этапу. В противном случае процедура будет вызываться, пока все помеченные вершины не станут просмотренными, и если сток сети не был достигнут – увеличивающая цепь не может быть построена и по теореме Форда-Фалкерсона имеющийся поток сети является максимальным.
Этап 2. Изменение потока.
Процедура изменения потока дуги.
Возьмем узел x. Если он имеет метку [y, +, e], то увеличим поток по дуге (y, x) на e. Если он имеет метку [y, -, e], то уменьшим поток по дуге (y, x) на e. Если y не является источником, то вызовем процедуру для узла y.
Эта процедура, будучи вызвана для стока сети, позволяет пройти по найденной увеличивающей цепи к стоку, изменяя поток на ее дугах.
Следует особо отметить, что узлы, имеющие статус “помеченных”, больше не участвуют в процессе поиска увеличивающей цепи, весьма эффективно с вычислительной точки зрения.[1][1]
Алгоритм Форда-Фалкерсона гарантирует нахождение максимального потока только в сетях с целочисленными пропускными способностями. На практике “чистый” алгоритм Форда-Фалкерсона не применяется, т.к. оценка его производительности зависит от величины пропускных способностей дуг сети. Все дело в том, что в нем не дается каких либо правил выбора увеличивающей цепи.
Рассмотрим сеть на рис. 1. Предположим, что реализован алгоритм, отдающий предпочтение увеличивающим цепям максимальной длины. В этом случае на первом шаге мы пустим дополнительный поток по цепи (0,1),(1,2),(2,3).

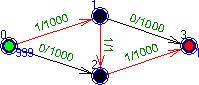
рис. 1 рис. 2
На втором шаге выберем цепь (0,2),(2,1),(1,3). Так как дуга (2,1) несогласованна, величина пущенного по ней потока будет вычитаться из величины потока, полученного на предыдущем шаге. Мы получили сеть (рис. 3) практически эквивалентную исходной.

рис. 3
Очевидно, что для нахождения максимального потока понадобиться 1000 итераций! В то время, как если бы мы на первом шаге выбрали цепь (0,1),(1,3), то результат был бы получен за одну итерацию! На практике, величина пропускных способностей часто зависит от единиц измерения, и может принимать огромные значения. Если же допустить иррациональные пропускные способности дуг, то можно привести пример невычислимой сети [4]. Величина потока в такой сети не превысит даже четверти истинного значения. Подобная неопределенность длилась не долго, уже в начале 70-х г. были предложены сразу 2 правила выбора увеличивающих цепей, которые существенно улучшают алгоритм Форда-Фалкерсона.
Действуя по нашему методу, на каждом шаге мы выбираем произвольный дополняющий путь и увеличиваем поток, добавляя поток величины остаточной пропускной способности вдоль выбранного пути.
Время работы алгоритма зависит от того, как ищется дополняющий путь. Логично было бы искать его методом поиска в ширину, в этом случае путь будет кратчайшим из всех дополняющих путей(если длину каждого ребра считать единицей). Эта реализация метода Форда-Фалкерсона называется алгоритмом Эдмондса-Карпа. Время его работы есть O(V*E2).
К задаче о максимальном потоке в сети сводятся некоторые комбинаторные задачи — например задача о максимальном паросочетании в двудольном графе (см. соотв. визуализатор).
Чтобы решить эту задачу, добавляем к имеющемуся графу две вершины, одна из которых будет истоком, а вторая — стоком и соединяем соотв. исток с каждой вершиной одной доли, а сток — с каждой вершиной другой. При этом все пропускные способности ставим одинаковые — например по 1, а все ребра превращаем в дуги, направленные от истока к стоку. Если найти в получившейся сети максимальный поток, тогда величина его будет равна мощности максимального паросочетания, а дуги, по которым будет течь этот максимальный поток и будут насыщенными ребрами максимального паросочетания.
Математическая постановка задач оптимизации. Критерии оптимизации. Виды ограничений. Классификация задач: задачи безусловной и условной оптимизации, одномерной и многомерной оптимизации, задачи нелинейного, линейного, целочисленного программирования, задачи оптимизации на сетях.
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например: - количество продукции - "расход сырья" – кол-во продукции - "качество продукции" Выбор компромиссного вариан
Последнее изменение этой страницы: 2017-09-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...