Постановка задачи безусловной оптимизации ФНП. Метод многогранника. Алгоритм метода.

Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности. ПЗ: àmin. Найти хотя бы один локальный мин.функции , (существует или удовлетворяет определенному условию) с заданной точностью:

1. по решению , где -приблизиженное значение, 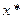-лок. Мин.

2. по градиенту ,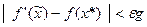

Метод многогранника (Нелдера и Мида).

Основан на построении симплекса. Суть: строится простейший многогранник (треугольник) в центре х0, Дальше вершины нумеруются По принципу худшая- лучшая вершина.В данном случае худшая -3, лучшая -1.

И так далее на каждую лучшую точу строится треугольник

Алгоритм:

1. Вводим начальную точку х0, размер R, точность по х , точность по значению функции , точность по производной . Дана функция àmin, коэффициент шагов х.

2. Строим многогранник (симплекс) с центром в точке х0 и размером R.

, где <i>-i-я вершина i=1...n

3. Расчет значений функций

В точке симплекса i=0..n

4. Переупорядочиваем вершины симплекса

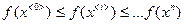Редукция симплекса – стягивание всех вершин

4а. Самая лучшая точка симплекса .

Оценки значения критерия останова:

1)Размер симплекса меньше по значению точности

,

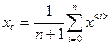
2)Отключение от хорошей точки до плохой точки

3)Оценка производной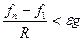

5. коэффициенты . Делаем пробный шаг , где xc – центр отображения. ,

6. Принимаем решение: делаем растягивающий шаг или сжимающий шаг, если ,то делаем шаг , , if , then h=p, else h=f

7. Иначе если шаг хуже, то в этом случае сравниваем значение функции с самой худшей точкой , то h=α, а если он еще хуже, то , if , then h=γ, else редукция симплекса в самой лучшей точке х0

, и переупорядочиваем вершины (п.4а), а потом возвращаемся к п.5

8. Делаем шаг (нормированный шаг) h , 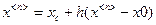, , мы получаем новую точку.

^9.Теперь переупорядочиваем точки с учетом новой точки х^<n>

10. идем к п.4а

11. постановка задачи безусловной оптимизации ФНП. Метод Монтер-Карло. Алгоритм метода. Основные параметры метода.

ПЗ: àmin. Найти хотя бы один локальный мин.функции , (существует или удовлетворяет определенному условию) с заданной точностью:

1.по решению , где -приблизиженное значение, 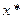-лок. Мин.

2.по градиенту ,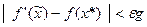

Метод Монтер-Карло

Суть: задаем начальную точку и куб с n количеством разбросанных точек, если х1 лучше х0, то рис следующий квадрат и разбрасываем снова точки и ищем наилучшую,если ее нет то уменьшаем область R(квадрата) и т д

Алгоритм:

1. Ввод начальной точки х0, размера R, количество точек N, которые бросаем, точность Ех, Еf

2. Вокруг начальной точки разбрасываем N точек в куб размером R.

For i=1,N, теперь для каждой точки, рассчитываем случайное отклонение от х0

For j=1,n, где n- размерность задачи.

Δj= - R/2+rnd R, где rnd – число в интервале [0,1]

x ^<i> =x0+Δ сгенерировали точки

3.Расчитываем , при i=1,N

4. Ищем х-мин. fmin=f(xmin), xmin= ?

5. Локализуем удачность шага, если fmin<f(x0), то шаг удачен x0=xmin, иначе шаг не удачен, то уменьшаем R=R/2

6. если не удовлетворяется условие Ех, то идем к п.2

7.выводим х0, f(x0), R, Δf

Критерии останова сходимости метода:

1)R<Ex

2) Δf<Ef, где Δf-значение получившейся функции f ^n-1 – f ⁿ

Δf=f ^n-1 – f ⁿ >0

3) Δf/ Δr <Eg

Постановка задачи безусловной оптимизации ФНП. Градиентные методы и метод наискорейшего спуска.

ПЗ: àmin. Найти хотя бы один локальный мин.функции , (существует или удовлетворяет определенному условию) с заданной точностью:

1.по решению , где -приблизиженное значение, 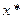-лок. Мин.

2.по градиенту ,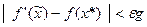

К методам 1 –го порядка (градиентным методам).

1)метод наискорейшего спуска

2) градиентный с дробным шагом

3) овражный

В том случае, когда доступна только первая производная, то в качестве направления спуска естественно рассматривать антиградиентное направление. Методы, использующие в качестве направления поиска вектор-градиент, называют градиентными. Алгоритм этих методов отличается от предыдущего отсутствием вычисления вторых производных и добавлением пункта вычисления длины шага.

Метод наискорейшего спуска

Самый известный из семейства градиентных методов это метод наискорейшего спуска. Он так назван потому, что спуск вдоль антиградиентного направления осуществляется в точку минимума.

Алгоритм:

1.вводим x0 (начального приближения), eg-точность по градиенту конечного решения и e1g точность по производной по направлению).

2.Пока /f ’(x0)/<eg, n=0

2.1.вычисляем направление спуска Pk= - f ’(x0)= - grad (x0), при к=к+1

2.2 Производим одномерную оптимизацию поиска из точки х0 вдоль направления Рк, то х1=argmin f(x0+αPk) c точностью e1g (e1g≤eg)

2.3 Критерии останова

Δх=х1-х0, если /Δx/<ex, то аварийный выход, застряли х0, f(x0), f ’(x0), /Δx/-длина последнего шага

2.4х0=х1

3. вывод полученного значения х0, f(x0), f ’(x0)