
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
ПЗ безусловной оптимизации ФНП. Методы второго порядка. Метод Ньютона с дробным шагом. Алгоритм выбора длины шага.
ПЗ: Дана непрерывно дифференцируемая функция 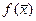 n переменных. Необходимо найти хотя бы одну точку локального оптимума этой функции:
n переменных. Необходимо найти хотя бы одну точку локального оптимума этой функции:
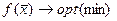 , где
, где  ,
, 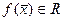 ,
, 
К методам 2-го порядка относятся метод Ньютона и метод Ньютона с дробным шагом.
Метод Ньютона с дробным шагом: Делаем пробный шаг, если удовлетворяет условиям, то идем дальше, если нет, то делаем дробный шаг.
Ньютоновское направление: 
 ,
, 
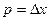



 шаг
шаг
Перед расчетом оптимума необходимо найти первую и вторую производные функции:
g(x) = df/dx 
Алгоритм метода Ньютона состоит в следующем.
1. В начальной точке х0 вычисляется вектор p
2. На k-й итерации определяются шаг αи точка х[k+1].
3. Вычисляется величина f(х[k+1]).
4. Проверяются условия выхода из подпрограммы, реализующей данный алгоритм. Эти условия аналогичны условиям выхода из подпрограммы при методе наискорейшего спуска. Если эти условия выполняются, осуществляется прекращение вычислений. В противном случае вычисляется новое направление р[k+1] и осуществляется переход к следующей итерации.
Количество вычислений на итерации методом Ньютона, как правило, значительно больше, чем в градиентных методах. Это объясняется необходимостью вычисления и обращения матрицы вторых производных целевой функции. Однако на получение решения с достаточно высокой степенью точности с помощью метода Ньютона обычно требуется намного меньше итераций, чем при использовании градиентных методов. В силу этого метод Ньютона существенно более эффективен.

Определение длины шага:
1. α:=1
2. while f(x+p* α)-f(x)>=0 уменьшаем шаг α:= α*γ
Величина шага α выбирается из условия минимума функции f(х) по α в направлении движения, т. е. в результате решения задачи одномерной минимизации: 
Общая постановка задачи условной оптимизации. Постановки задач линейного и целочисленного программирования. Необходимые и достаточные условия оптимальности ЗЛП.
ПЗ: Дана линейная функция L(x1,x2,...,xn) n переменных. Необходимо найти точку оптимума этой функции: L(x) ---> opt ,
при ограничениях: Ax-b>= 0 или  , i=1...m.
, i=1...m.
где x = (x1,x2,...,xn).
1) 
 при ограничении вида
при ограничении вида
2) 
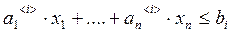
3) 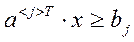

4) 
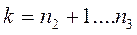
1) 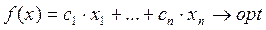 при ограничении вида
при ограничении вида






Общая и стандартная постановки ЗЛП. Переход от общей постановки задачи к стандартной.
Общая: Дана линейная функция L(x1,x2,...,xn) n переменных. Необходимо найти точку оптимума этой функции: L(x) ---> opt ,
при ограничениях: Ax-b>= 0 или  , i=1...m.
, i=1...m.
где x = (x1,x2,...,xn).
Стандартная:  Ax=b
Ax=b 




Для приведения задачи к стандартному виду: ввести переменные и записать целевую функцию и ограничение задачи.
Метод и алгоритм решения стандартной задачи линейного программирования и способы сведения любой задачи линейного программирования к стандартной форме, которая состоит в следующем. Задана система m линейных алгебраических уравнений с n неизвестными:

 (3.7)
(3.7)
и линейная функция относительно переменных х1, х2, ¼, хn:
 (3.8)
(3.8)
Требуется найти такие неотрицательные значения переменных х1, х2, ¼, хn, которые бы удовлетворяли системе линейных уравнений (3.7) и, кроме того, обращали в максимум линейную функцию (3.8).
Заметим, что если по условиям задачи требуется отыскать минимум функции L, записанной в виде (3.8), то задачу можно свести к задаче максимизации функции L¢, связанной с функцией L так:
L¢ = - L = -c1x1 - c2x2 - ¼ - cnxn. (3.9)
Максимум функции (3.9) и минимум функции (3.8) будут достигаться при одном и том же наборе переменных (х1,х2, ¼, хn), удовлетворяющих условиям неотрицательности переменных и уравнениям (3.7), областью определения задачи.
Пример перехода от общей задачи к стандартной в 20 вопросе.
Графическое решение ЗЛП. Основные понятия и идея решения задачи.
Если число неизвестных в задаче линейного программирования равно двум, т.е. n = 2, то ее можно решить графическим методом. Кроме того, графический метод дает геометрическую интерпретацию решения ЗЛП.
Пример:
Задача: Предприятие производит краски 2-х видов: I – для внутренних работ, E – для внешних работ. A,B – исходные продукты, использующиеся для производства I,E.
Доход от реализации 1т краски I – 2000$, E – 3000$
Коэффициенты расхода исходных продуктов A и B на производство 1т краски I и E:
| I | E | Суточный запас, тонн | |
| A | |||
| B |
Известно, что суточная потребность краски для внутренних работ не превышает 2т, т.е. суточный спрос на I <=2т. Суточный спрос I не превышает суточного спроса на E больше чем на 1т.
Найти: оптимальный суточный план производства красок, максимизирующий ожидаемый максимальный доход.
Математическая постановка задачи:
Обозначим XI(т/сут) – краски I ; XE(т/сут) – краски E.
Целевая функция: 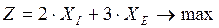 - ожидаемый максимальный доход
- ожидаемый максимальный доход
Ограничения на запас продукта А: 
Ограничения на запас продукта В: 
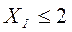 ,
,  ,
, 
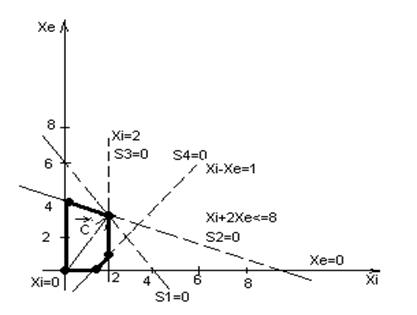
При XI=0 и XE=0 
Найдем точку пересечения:

-3XI=-4 XI=4/3 XE=10/3
Z(4/3;10/3)=38/3 Z(0;4)=12
Идея решения задачи: Используя Симплекс-метод, получить последовательность базисных решений и оптимальное решение.
Целевая функция представляет собой взвешенную линейную сумму от неизвестных переменных xi вида: Z=c*xi c- вектор целевой функции.
Ограничения, накладываемые на область возможных решений, имеют вид линейных равенств или неравенств: 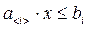 где ai, bi - известные величины, причем величины aj, xi, bi положительные.
где ai, bi - известные величины, причем величины aj, xi, bi положительные.
Допустимым решением задачи линейного программирования будем называть любую совокупность переменных
х1³ 0, х2³ 0, ¼ , хn ³0, (3.10)
удовлетворяющих уравнениям

Оптимальным решением  будем называть то из допустимых решений, для которого линейная форма Z обращается в максимум (минимум).
будем называть то из допустимых решений, для которого линейная форма Z обращается в максимум (минимум).
Последнее изменение этой страницы: 2017-09-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...