
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Понятие о моделировании случайных функций
Для моделирования случайных функций используют два способа. В первом из них применяются специальные физические датчики, вырабатывающие непрерывные реализации случайной функции. Физические датчики с помощью специальных фильтров преобразуют собственные шумы в случайные функции с заданными характеристиками.
В основе второго способа моделирования случайных функций лежит использование случайных чисел. При этом получают значения изолированных точках. Сущность способа состоит в том, что воспроизведение реализации случайной функции сводится к моделированию системы коррелированных случайных величин.
3.2. Моделирование систем массового обслуживания
с использованием метода Монте-Карло
Рассмотренные в работе «Бережная Е.В., Бережной В И. Математические методы моделирования экономических систем: учеб. пособие. – М.: Финансы и статистика, 2003. – 368 с.» аналитические методы анализа систем массового обслуживания (СМО) исходят из предположения, что входящие и исходящие потоки требований являются простейшими. Зависимости, используемые в этих методах для определения показателей качества обслуживания, справедливы лишь для установившегося режима функционирования СМО. Однако в реальных условиях функционирования СМО имеются переходные режимы, а входящие и исходящие потоки требований являются далеко не простейшими. В этих условиях для оценки качества функционирования систем обслуживания широко используют метод статистических испытаний (метод Монте-Карло).Основой решения задачи исследования функционирования СМО в реальных условиях является статистическое моделирование входящего потока требований и процесса их обслуживания (исходящего потока требований).
Для решения задачи статистического моделирования функционирования СМО должны быть заданы следующие исходные данные:
v описание СМО (тип, параметры, критерии эффективности работы системы);
v параметры закона распределения периодичности поступлений
требований в систему;
v параметры закона распределения времени пребывания требования в очереди (для СМО с ожиданием);
v параметры закона распределения времени обслуживания требований в системе.
Решение задачи статистического моделирования функционирования СМО складывается из следующих этапов.
1.Вырабатывают равномерно распределенное случайное число 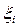 .
.
2.Равномерно распределенные случайные числа преобразуют в
величины с заданным законом распределения:
ü интервал времени между поступлениями требований в систему (  ):
):
ü время ухода заявки из очереди (для СМО с ограниченной длиной очереди);
ü длительность времени обслуживания требования каналами (  )
)
3. Определяют моменты наступления событий:
ü поступление требования на обслуживание;
ü уход требования из очереди;
ü окончание обслуживания требования в каналах системы.
4. Моделируют функционирование СМО в целом и накапливают статистические данные о процессе обслуживания.
5. Устанавливают новый момент поступления требования в систему, и вычислительная процедура повторяется в соответствии с изложенным.
6. Определяют показатели качества функционирования СМО путем обработки результатов моделирования методами математической статистики.
Методику решения задачи рассмотрим на примере моделирования СМО с отказами.
Пусть система имеет два однотипных канала, работающих с отказами, причем моменты времени окончания обслуживания на первом канале обозначим через  , на втором канале – через t2i. Закон распределения интервала времени между смежными поступающими требованиями задан плотностью распределения f1(tT). Продолжительность обслуживания также является случайной величиной с плотностью распределения f2 (tT)-
, на втором канале – через t2i. Закон распределения интервала времени между смежными поступающими требованиями задан плотностью распределения f1(tT). Продолжительность обслуживания также является случайной величиной с плотностью распределения f2 (tT)-
Процедура решения задачи будет выглядеть следующим образом:
1. Вырабатывают равномерно распределенное случайное число 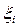 .
.
2. Равномерно распределенное случайное число преобразуют в
величины с заданным законом распределения, используя формулы
табл. 3.1. Определяют реализацию случайного интервала времени (  ) между поступлениями требований в систему.
) между поступлениями требований в систему.
3. Вычисляют момент поступления заявки на обслуживание:
 .
.
4. Сравнивают моменты окончания обслуживания предшествующих заявок на первом  и втором
и втором  каналах.
каналах.
5. Сравнивают момент поступления заявки t,- с минимальным моментом окончания обслуживания (допустим, что  :
:
а) если  , то заявка получает отказ и вырабатывают новый момент поступления заявки описанным способом;
, то заявка получает отказ и вырабатывают новый момент поступления заявки описанным способом;
б) если  , то происходит обслуживание.
, то происходит обслуживание.
6. При выполнении условия 5 б) определяют время обслуживания i-й заявки на первом канале  путем преобразования случайной величины
путем преобразования случайной величины 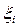 , в величину (время обслуживания i-й заявки) с заданным законом распределения.
, в величину (время обслуживания i-й заявки) с заданным законом распределения.
7. Вычисляют момент окончания обслуживания i-й заявки на первом канале tu — [/|(j_d + Д/|,-1-
8. Устанавливают новый момент поступления заявки, и вычислительная процедура повторяется в соответствии с изложенным.
9. В ходе моделирования СМО накапливаются статистические
данные о процессе обслуживания.
10. Определяют показатели качества функционирования системы путем обработки накопленных результатов моделирования методами математической статистики.
3.3. Моделирование потоков отказов элементов сложных
технических систем
Под сложной технической системойбудем понимать систему, состоящую из элементов (два и более). Отказ одного из элементов системы приводит к отказу системы в целом.
Рассмотрим последовательность замен некоторого определенного элемента Z данного наименования. Эксплуатация каждого нового элемента начинается с момента окончания срока службы предыдущего. Первый элемент отрабатывает время  , второй –
, второй –  , третий –
, третий –  и т. д.
и т. д.
Случайная ситуация, сложившаяся в к-мопыте (ситуации) для элемента Z, показана на рис. 3.3.

Рис. 3.3. Временная эпюра случайной ситуации при k-м опыте
в случае мгновенного восстановления отказавшей системы путем замены элемента
На рис. 3.3 видно, что система начинает свою работу в момент времени t = 0 и, отработав случайное время Δt1k, выходит из строя в момент t1k = Δtlk. В этот момент система мгновенно восстанавливается (здесь можно считать, что восстановление происходит мгновенно) – элемент заменяется – и снова работает случайное время Δt2k. По истечении некоторого времени система (элемент) вновь
выходит из строя в момент  и вновь мгновенно восстанавливается.
и вновь мгновенно восстанавливается.
Считают, что интервалы времени между отказами Δtik, Δt2k, ..., Δtpk представляют собой систему взаимно независимых случайных величин с плотностями распределения наработок между отказами
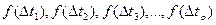 .
.
Моменты отказов или восстановлений образуют в каждом к-мопыте (испытании) ряд чисел по следующему правилу:
 (3.11)
(3.11)
или
 , (3.12)
, (3.12)
где tlk – время работы (наработка) элемента до i-го отказа в к-м опыте, час,  ; Δtik – время работы (наработка) элемента между (i- 1)-м и i-м отказами в к-йреализации, час,
; Δtik – время работы (наработка) элемента между (i- 1)-м и i-м отказами в к-йреализации, час,  .
.
Числа t1k, t2k, ..., tpk образуют случайный поток, который называется процессом восстановления.Этот процесс является различным для различных элементов и продолжается до окончания срока службы системы. Изучением таких процессов занимается теория восстановления.
Из большого количества различных процессов восстановления
для исследования надежности элементов технической системы (как
неремонтируемых, так и ремонтируемых) используют три типа процессов:
Ø простой, при котором все функции распределения наработок
до первого и между последующими отказами Fi(t) равны;
Ø общий, при котором вид функции распределения наработки
до первого отказа элемента, установленного в системе заводом - изготовителем, отличается от вида функций распределения наработок элементов при последующих заменах, т. е.  , i = 2, 3, 4, ...;
, i = 2, 3, 4, ...;
Ø сложный, при котором все функции распределения  различны.
различны.
Основной характеристикой процесса восстановления является функция восстановления Ω(t) и ее дифференциальная характеристика – плотность восстановления ω(t), определяемые по следующим формулам:
 ; (3.13)
; (3.13)
 , (3.14)
, (3.14)
где fn(t) и Fn(t) — соответственно плотность и функция распределения наработки до n-го отказа.
В случае независимости наработок между отказами функции распределения Fn(t) наработок до n-го отказа находятся путем последовательного применения правила свертки для суммы двух случайных величин:
 (3.15)
(3.15)
Анализ и классификация методов расчета параметра и ведущей функции потока отказов приведены в книге авторов (Бережной В.И., Бережная Е.В. Методы и модели управления материальными потоками микрологистической системы автопредприятия. – Ставрополь: Интеллект-сервис, 1996.). Следует отметить, что сложность получения аналитических выражений для  и
и  по формулам (3.13), (3.14) состоит в том, что свертка (3.15) лишь для некоторых законов распределения вычисляется в конечном виде. Использование аналитических методов расчета плотности
по формулам (3.13), (3.14) состоит в том, что свертка (3.15) лишь для некоторых законов распределения вычисляется в конечном виде. Использование аналитических методов расчета плотности  и функции восстановления
и функции восстановления  ограничено из-за сложности математической формализации применяемых стратегий восстановления работоспособности технических систем и необходимости учета множества факторов, влияющих на замену элемента в системе. В этих условиях наиболее эффективным методом расчета
ограничено из-за сложности математической формализации применяемых стратегий восстановления работоспособности технических систем и необходимости учета множества факторов, влияющих на замену элемента в системе. В этих условиях наиболее эффективным методом расчета  и
и  является метод Монте-Карло.
является метод Монте-Карло.
Расчет ведущей функции и параметра потока отказов этим методом в случае простого, общего или сложного процессов производится в следующем порядке.
По известным законам распределения наработок элементов с использованием формул преобразования (табл.3.1) моделируются массивы случайных величин Δtjk между (i - 1)-м и i-м отказами. Размерность каждого массива равна N.
Далее вычисляются значения наработок до i-го отказа tik по следующим формулам:
 , (3.16)
, (3.16)
 , (3,17)
, (3,17)
где i – номер отказа,  ; k – номер реализации при моделировании,
; k – номер реализации при моделировании,  ;
; 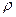 – максимальное число отказов элемента, получаемое в k-й реализации случайного процесса.
– максимальное число отказов элемента, получаемое в k-й реализации случайного процесса.
Затем полученные случайные величины наработок tik группируются по интервалам времени.
Номера интервалов, в которые попадают моменты возникновения отказов  , определяются по формуле:
, определяются по формуле:
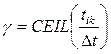 . (3,18)
. (3,18)
где  – наименьшее целое число, не менее
– наименьшее целое число, не менее  ;
;  - величина интервала времени.
- величина интервала времени.
Параметр и ведущая функция потока отказов в j-м интервале времени определяется по следующим формулам:
 ; (3,19)
; (3,19)
 , (3,20)
, (3,20)
где nij – число попаданий случайной наработки до i-го отказа tik в j-й интервал времени (  )за N реализаций.
)за N реализаций.
 ; (3.21)
; (3.21)
 . (3.22)
. (3.22)
где h – максимальное число интервалов времени.
Методика расчета параметра u>(t) и ведущей функции нестационарного потока отказов с использованием метода статистических испытаний подробно рассмотрена в книге авторов1.
Пример 3.7.Законы распределения наработок элемента системы до первого и второго отказов и соответствующие параметры этих законов приведены в следующей таблице:
| № отказа | Закон распределения | Параметры закона | |

| b | ||
| Вейбула | 1,4 | 45,8 | |
| Экспоненциальный | 0,30 | - |
Определите номера временных интервалов, на которых произойдут первый и второй отказы в ходе первого опыта (испытания) (Δt = 1 час).
Решение
1. Выберем равномерно распределенное случайное число. Допустим  = 0,725.
= 0,725.
2. Вычислим случайные значения наработок на отказ элемента,
используя формулы табл. 3.1.
 час.;
час.;
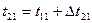 ;
;
 час.;
час.;
 час.
час.
3. Определим номер временного интервала, на котором произойдут отказы
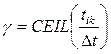
первый отказ
 ;
;
второй отказ
 .
.
В ходе первой реализации элемент системы первый раз откажет на 21-м временном интервале, а второй отказ произойдет на 22-м временном интервале.
ЗАДАЧИ
3.1. Периодичность поступления заявок на обслуживание подчинена показательному закону распределения. Средний интервал между поступлениями заявок в систему равен  =2 час. Определите последовательность значений продолжительности интервалов между поступлениями заявок. Число реализаций равно 10.
=2 час. Определите последовательность значений продолжительности интервалов между поступлениями заявок. Число реализаций равно 10.
Время обслуживания работника предприятия кассой бухгалтерии является случайной величиной, распределенной в соответствии с законом Вейбула. Среднее время обслуживания  = 3 мин., среднее квадратическое отклонение равно
= 3 мин., среднее квадратическое отклонение равно  = 2 мин. Требуется смоделировать случайную величину, отвечающую этим условиям. Число реализаций принять равным 10.
= 2 мин. Требуется смоделировать случайную величину, отвечающую этим условиям. Число реализаций принять равным 10.
При обработке экспериментальных данных было установлено, что время, расходуемое на станции технического обслуживания автомобилей для замены двигателя, распределено по нормальному закону, параметры которого  = 2,8 час. на один двигатель и
= 2,8 час. на один двигатель и  = 0,6 час. Требуется смоделировать для отмеченных условий случайную величину – время X, расходуемое для замены двигателя. Число реализаций принять равным 5.
= 0,6 час. Требуется смоделировать для отмеченных условий случайную величину – время X, расходуемое для замены двигателя. Число реализаций принять равным 5.
Время проверки приемки квартального отчета инспектором
налоговой службы (t) величина случайная, распределенная в соответствии с законом Вейбула. Среднее время проверки и приемки равно  = 20 мин. Коэффициент вариации величины t равен Vt = 0,52. Требуется смоделировать для заданных условий случайные числа t (число реализаций принять равным 10).
= 20 мин. Коэффициент вариации величины t равен Vt = 0,52. Требуется смоделировать для заданных условий случайные числа t (число реализаций принять равным 10).
Среднее число исправных станков в токарном цехе на за
воде равно  = 6. Среднее квадратическое отклонение
= 6. Среднее квадратическое отклонение 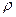 =2,2. Требуется смоделировать число исправных станков в цехе (число реализаций равно 5) при условии, что случайная величина X имеет гамма-распределение.
=2,2. Требуется смоделировать число исправных станков в цехе (число реализаций равно 5) при условии, что случайная величина X имеет гамма-распределение.
Вероятность замены неисправной детали на новую при ремонте автомобиля в каждом испытании р=0,63. Смоделировать пять (5) испытаний и определить последовательность замены детали на новую или восстановленную.
При испытании могут иметь место зависимые и совместные три события: работает только первый кассир по выдаче заработной платы, работает только второй кассир, работают оба кассира. При этом известно, что вероятность работы первого кассира равна 0,6; вероятность работы второго кассира равна 0,7; вероятность работы двух кассиров равна 0,4. Смоделировать возможность реализации двух событий: работает только первый кассир; работает только второй кассир в трех испытаниях.
Известны законы распределения наработок элемента системы до первого и второго отказов. Средние значения и средние квадратические отклонения наработок приведены в следующей таблице:
| № отказа | Закон распределения | Среднее значение наработки, час. | Среднее квадратическое отклонение наработки, час. |
| Вейбула | |||
| Гамма - распределение |
Определите параметр и ведущую функцию потока отказов элемента по интервалам времени (Δt = 10 час). Число реализаций N= 10.
Используя условия задачи 4.8, определите номер интервала, в который попадет максимальное количество отказов.
Система имеет два элемента. Средняя периодичность первого элемента  = 60 час, второго элемента –
= 60 час, второго элемента –  = 85 час. Периодичности отказа первого и второго элементов – случайные величины, подчиненные экспоненциальному закону распределения. Определите параметр и функцию распределения потока отказов системы по интервалам времени Δt = 8 час. Число реализаций N = 10.
= 85 час. Периодичности отказа первого и второго элементов – случайные величины, подчиненные экспоненциальному закону распределения. Определите параметр и функцию распределения потока отказов системы по интервалам времени Δt = 8 час. Число реализаций N = 10.
Используя условия задачи 4.10, определите номера интервалов, в которые попадут максимальные количества отказов первого, второго элементов и в целом всей системы.
Пусть при испытании могут иметь место зависимые и совместные события А и D. Известно, что вероятности появления событий равны Р(А) = 0,6; P(D) – 0,3, а также вероятность совместного появления событий А и D: P(AD) = 0,4. Смоделируйте появление событий А и D в пяти испытаниях.
Периодичность проверки предприятий налоговой инспекции – величина случайная (Δt), подчиняющаяся закону гамма-распределения. Средний интервал проверки  = 2,5 мес. Коэффициент вариации величины Δt равен V = 0,38. Требуется смоделировать для заданных условий возможные моменты проверок предприятия налоговой инспекцией (число реализаций принять равным 10).
= 2,5 мес. Коэффициент вариации величины Δt равен V = 0,38. Требуется смоделировать для заданных условий возможные моменты проверок предприятия налоговой инспекцией (число реализаций принять равным 10).
Используя условия задачи 4.13, определите количество проверок налоговой инспекцией за первый год работы предприятия.
Среднее число работающих машин на заводе  = 25. Коэффициент вариации числа работающих V=0,6. Требуется смоделировать число работающих машин на заводе (число реализаций равно 10). Случайная величина X имеет распределение Вейбула.
= 25. Коэффициент вариации числа работающих V=0,6. Требуется смоделировать число работающих машин на заводе (число реализаций равно 10). Случайная величина X имеет распределение Вейбула.
После каждой проверки предприятия налоговой инспекцией вероятность появления необходимости аудиторской проверки данного предприятия Р = 0,72. Смоделируйте шесть испытаний. Определите последовательность проведения различных проверок предприятия.
Часть 4
МЕТОДЫ И МОДЕЛИ КОРРЕЛЯЦИОННОГО
РЕГРЕССИОННОГО АНАЛИЗА
Общие сведения
Большинство явлений и процессов в экономике находятся в постоянной взаимной и всеохватывающей объективной связи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль в экономике. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ, который является методическим инструментарием при решении задач прогнозирования, планирования и анализа хозяйственной деятельности предприятий.
Различают два вида зависимостей между экономическими явлениями и процессами:
 функциональную;
функциональную;
 стохастическую (вероятностную, статистическую).
стохастическую (вероятностную, статистическую).
В случае функциональной зависимости имеется однозначное отображение множества А на множество В. Множество А называют областью определения функции, а множество В – множеством значений функции.
Функциональная зависимость встречается редко. В большинстве случаев функция (Y) или аргумент (Х) – случайные величины. X и У подвержены действию различных случайных факторов, среди которых могут быть факторы, общие для двух случайных величин.
Если на случайную величину X действуют факторы Z1, Z2, ..., V1, V2, а на Y – Zo, Z2, V1, V3 ..., то наличие двух общих факторов Z2 и V1 позволяет говорить о вероятностной или статистической зависимости между X и Y.
Определение.Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.
В частном случае статистическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание другой. В этом случае говорят о корреляции или корреляционной зависимости.
Статистическая зависимость проявляется только в массовом процессе, при большом числе единиц совокупности.
При стохастической закономерности для заданных значений зависимой переменной можно указать ряд значений объясняющей переменной, случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обусловливается тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.
В экономике приходится иметь дело со многими явлениями, имеющими вероятностный характер. Например, к числу случайных величин можно отнести: стоимость продукции, доходы предприятия, межремонтный пробег автомобилей, время ремонта оборудования и т. д.
Односторонняя вероятностная зависимость между случайными величинами есть регрессия. Она устанавливает соответствие между этими величинами.
Односторонняя стохастическая зависимость выражается с помощью функции, которая называется регрессией.
Перечислим различные виды регрессии.
1.Регрессия относительно числа переменных:
Ø простая регрессия — регрессия между двумя переменными;
Ø множественная регрессия — регрессия между зависимой пере
менной у и несколькими объясняющими переменными х}, х2, ...,
хт. Множественная линейная регрессия имеет следующий вид:
 , (4.1)
, (4.1)
где y – функция регрессии;
x1,x2,…,xm – независимые переменные;
a1,a2,…,am – коэффициенты регрессии;
a0 – свободный член уравнения;
m – число факторов, включаемых в модель.
2. Регрессия относительно формы зависимости:
Ø линейная регрессия, выражаемая линейной функцией;
Ø нелинейная регрессия, выражаемая нелинейной функцией.
3. В зависимости от характера регрессии различают следующие
ее виды:
Ø положительную регрессию. Она имеет место, если с увеличением (уменьшением) объясняющей переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются);
Ø отрицательную регрессию. В этом случае с увеличением или
уменьшением объясняющей переменной зависимая переменная уменьшается или увеличивается.
Ø Относительно типа соединения явлений различают:
Ø непосредственную регрессию. В этом случае зависимая и объясняющая переменные связаны непосредственно друг с другом;
Ø косвенную регрессию. В этом случае объясняющая переменная
действует на зависимую через ряд других переменных;
Ø ложную регрессию. Она возникает при формальном подходе к
исследуемым явлениям без уяснения того, какие причины обусловливают данную связь.
Регрессия тесно связана с корреляцией. Корреляцияв широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова. Если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляция.
Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется ее форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.
Корреляция, как и регрессия, имеет различные виды:
1. Относительно характера корреляции различают:
Ø положительную;
Ø отрицательную.
2. Относительно числа переменных:
Ø простую;
Ø множественную;
Ø частную.
3. Относительно формы связи:
Ø линейную;
Ø нелинейную.
4. Относительно типа соединения:
Ø непосредственную;
Ø косвенную;
Ø ложную.
Любое причинное влияние может выражаться либо функциональной, либо корреляционной связью. Но не каждая функция или корреляция соответствует причинной зависимости между явлениями. Поэтому требуется обязательное исследование причинно-следственных связей.
Исследование корреляционных связей мы называем корреляционным анализом, а исследование односторонних стохастических зависимостей — регрессионным анализом. Корреляционный и регрессионный анализ имеют свои задачи.
Последнее изменение этой страницы: 2017-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...