
Главная Случайная страница
Категории:
ДомЗдоровьеЗоологияРнформатикаРскусствоРскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиРкологияРРєРѕРЅРѕРјРёРєР°Рлектроника
Логические элементы и логические схемы
Основным логическим операциям, используемым РІ РР’Рњ, соответствуют следующие логические элементы, каждый РёР· которых имеет РґРІР° РІС…РѕРґР° (слева) Рё РѕРґРёРЅ выход (справа).

| 
| 
| 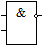
|
| дизъюнкция | конъюнкция | стрелка Пирса | штрих Шеффера |
Для отрицания отдельный элемент применяется редко, так как отрицание (обозначается кружком) может быть помещено как на входы
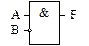
| F = A 
|
так и на выходы логических элементов

| F = 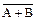 . .
|
Логические элементы реализуются аппаратно с помощью транзисторов, резисторов и т. п. Значению «истина» соответствует наличие напряжения на входах и на выходах, значению «ложь» – его отсутствие.
Логические элементы соединяются между собой и подсоединяются к входам, соответствующим переменным X, Y, Z, и образуют логическую схему. Как правило, логическая схема имеет один выход.
Пример 6.7. Построить логическую схему, реализующую упрощенную функцию из примера 6.1.
Решение. Каждый логический элемент имеет только два входа, поэтому перегруппируем слагаемые:
f(X, Y, Z) = X + Y  +
+ 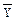 Z = (X + Y
Z = (X + Y  ) +
) +  Z.
Z.
Запишем схему, соответствующую логической функции (СЂРёСЃ. 6.1). Черные точки РЅР° соединителях элементов обозначают разветвление, чтобы отличать его РѕС‚ наложения соединителей. □

Рис. 6.1. Логическая схема, соответствующая
функции f(X, Y, Z) = X + Y  +
+  Z
Z
Перед построением логической схемы функцию минимизируют, чтобы получить схему с минимальным количеством элементов.
Пример 6.8. Построить функцию, соответствующую схеме
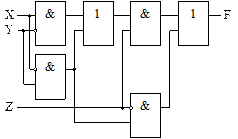
Минимизировать функцию и по ней построить логическую схему.
Решение. Выпишем функцию, соответствующую схеме:
f(X, Y, Z) = (X  +
+ 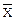 Y)Z +
Y)Z + 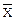 Y
Y  .
.
Минимизируем функцию по методу Блейка, для этого приведем ее к виду суммы произведений – раскроем скобки:
f(X, Y, Z) = (X 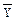 +
+ 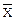 Y)Z +
Y)Z + 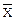 Y
Y  = X
= X 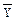 Z +
Z + 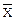 YZ +
YZ + 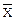 Y
Y  .
.
Перейдем ко второму этапу минимизации – применим операцию склеивания:
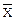 YZ +
YZ + 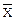 Y
Y  =
= 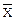 YZ +
YZ + 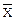 Y
Y  +
+ 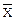 Y.
Y.
В результате второго этапа получим
f(X, Y, Z) = X 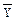 Z +
Z + 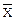 YZ +
YZ + 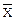 Y
Y  +
+ 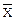 Y.
Y.
Перейдем к третьему этапу – применим операцию поглощения:
f(X, Y, Z) = X 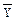 Z +
Z + 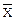 Y.
Y.
Функция минимизирована. Построим по ней логическую схему (рис. 6.2).
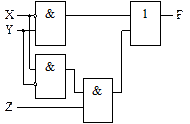
Рис. 6.2. Логическая схема, соответствующая
функции f(X, Y, Z) = X 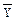 Z +
Z + 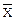 Y
Y
Р’ результате получена логическая схема, число элементов которой меньше, чем Сѓ РёСЃС…РѕРґРЅРѕР№. □
Количество входов логического элемента называется коэффициентом объединения (Коб). У всех рассмотренных элементов коэффициент объединения Коб = 2, но существуют элементы с коэффициентом объединения Коб = 3; 4; 8. Как правило, логические элементы не выпускаются отдельно, а интегрированы в некоторую логическую схему.
Для удешевления производства вместо логических элементов РґРІСѓС… типов Р Рё РЛРиспользуют элементы РѕРґРЅРѕРіРѕ типа Р-РќР• или РР›Р-РќР•. Чаще используют элементы Р-РќР•.
Пример 6.9. Построить логическую схему по функции в базисе NAND из примера 6.5.
Решение. Функция в базисе NAND имеет вид:
f(X, Y, Z) = (Y ½ Z) ½ (Y ½ X).
Логическая схема представлена РЅР° СЂРёСЃ. 6.3. □

Рис. 6.3. Логическая схема, соответствующая
функции f(X, Y, Z) = (Y ½ Z) ½ (Y ½ X)
Глава 7. Р—РќРђРќРРЇ. МОДЕЛРПРЕДСТАВЛЕНРРЇ Р—РќРђРќРР™
Знания и их особенности
Знания – это форма существования Рё систематизации познавательной деятельности человека, то, что РјС‹ знаем после изучения. Р’ РР’Рњ знания представляются РІ РІРёРґРµ схем, формул Рё текста РїРѕ определенным правилам. Представлению знаний РїСЂРёСЃСѓС‰ пассивный аспект: РєРЅРёРіР°, таблица, память РР’Рњ. Р’ системах искусственного интеллекта подчеркивается активный аспект представления: познание должно стать активной операцией, позволяющей РЅРµ только запоминать, РЅРѕ Рё извлекать воспринятые (приобретенные, усвоенные) знания для рассуждений РЅР° РёС… РѕСЃРЅРѕРІРµ.
Рассмотрим особенности знаний, отличающие их от данных.
1. Внутренняя интерпретируемость.
Каждая информационная единица имеет уникальный идентификатор, который позволяет системе искусственного интеллекта найти ее, например, для ответа на запрос, в которых этот идентификатор упомянут.
Пусть имеются следующие сведения о составе бригады цеха (табл. 7.1).
Таблица 7.1. Сведения о составе бригады цеха
| Фамилия | Специальность | Стаж | Разряд | Оклад |
| Попов | Слесарь | |||
| Сидоров | Токарь | |||
| Рванов | Токарь | |||
| Петров | Фрезеровщик |
Рнформация Рѕ том, РіРґРµ хранятся сведения Рѕ фамилиях, специальностях, стаже, разрядах Рё окладах называется протоструктурой информационных единиц. РЎ помощью данной протоструктуры можно найти необходимую информационную единицу Рё ответить РЅР° РІРѕРїСЂРѕСЃС‹ типа «Что системе известно Рѕ Петрове?В» или «Есть ли среди специалистов фрезеровщик?В».
2. Структурированность.
Структура информационных единиц представляет собой рекурсивную вложенность одних информационных единиц в другие. В данной таблице каждая строка содержит сведения об одном из работников, а вместе эти строки определяют состав бригады.
3. Связность
Между информационными единицами установлены связи различного типа. Отношения между информационными единицами могут быть декларативными или процедурными.
Пусть разряд определяется следующим образом. Если работник проработал 5 лет Рё менее, то РѕРЅ имеет 1 разряд, если 10 лет Рё менее – 2 разряд Рё С‚. Рґ. Рто пример декларативного отношения «ПРРР§РРќРђ – СЛЕДСТВРЕ».
Пусть оклад определяется по формуле
Оклад = Разряд ´ Ставка (= 2000).
Расчет оклада представляет СЃРѕР±РѕР№ отношение процедурного типа «АРГУМЕНТ – ФУНКЦРРЇВ».
Процедурные отношения между информационными единицами позволяют не хранить их отдельно, а получать по мере надобности из уже имеющихся информационных единиц.
Между информационными единицами могут устанавливаться и иные отношения, например, определяющие порядок выбора информационных единиц из структуры или указывающие на то, что две информационные единицы несовместимы друг с другом в одном описании.
4. Семантическая метрика.
Помимо отношений между информационными единицами можно установить меру близости по тематике или проблематике. На основе этих показателей формируются классы информационных единиц, что позволяет найти знания, близкие к уже найденным.
5. Активность.
Р’СЃРµ операции, выполняемые РР’Рњ, запускаются командами СЃ использованием данных, то есть данные пассивны, Р° команды активны. Р’ системах искусственного интеллекта, как Рё Сѓ человека, действия инициируются знаниями, имеющимися РІ системе. Знания предполагают целенаправленное использование информации, способность управлять информационными потоками для решения определенных задач.
Вышеперечисленные особенности отличают знания от данных. Однако эти особенности до сих пор не реализованы в полной мере в существующих системах.
Модели представления знаний
Представление знаний происходит в рамках той или иной системы представления знаний. Система представления знаний – это совокупность программных средств для хранения и обработки знаний. Система представления знаний выполняет следующие функции:
- хранение знаний о предметной области в соответствии с моделью представления знаний в базе знаний (БЗ);
- ввод новых знаний;
- проверка непротиворечивости хранимых знаний;
- удаление знаний;
- вывод новых знаний из уже имеющихся знаний;
- предоставление знаний пользователю.
Модель представления знаний – это способ записи знаний, предназначенный для отображения текущего состояния объектов некоторой предметной области и отношений между ними, а также изменение объектов и отношений.
Модель представления знаний может быть универсальной, то есть применимой для большинства предметных областей, или специализированной, то есть разработанной для конкретной предметной области. К основным универсальным моделям представления знаний относятся:
- логические модели;
- сетевые модели;
- продукционные модели;
- фреймовые модели.
Знания хранятся в базе знаний в соответствии с моделью представления знаний.
Логические модели
В основе логических моделей лежит понятие формальной теории, задаваемой четверкой:
S = < T, F, A, R >.
Рассмотрим компоненты формальной теории.
T – множество символов теории S, называемых термами и образующих алфавит теории. Конечная последовательность символов множества T называется выражением теории S.
F – подмножество выражений теории S, называемых формулами теории и построенных по синтаксическим правилам. Примерами правил могут быть праивла записи формул алгебры высказываний.
A – множество формул, называемых аксиомами теории S и являющихся априорно истинными формулами.
R – конечное множество отношений между формулами, называемые правилами вывода. Правила вывода позволяют получать новые формулы множества F за счет применения этих правил вывода к аксиомам или уже выведенным формулам.
Формальная система позволяет выводить новые правильные формулы множества F, применяя к аксиомам множества A и уже полученным формулам правила вывода множества R, то есть выводить из одних истинных высказываний новые истинные высказывания. Таким образом, в рамках формальной системы можно получить бесконечное число формул из небольшого числа исходных аксиом.
Вывод новых знаний в рамках логической модели представления знаний заключается в получении некоторого утверждения из имеющихся аксиом и правил вывода. Если в результате вывода утверждение получено, то оно считается истинным и является логическим следствием из аксиом.
Р’ этом случае задачей пользователя или программиста является описание предметной области совокупностью утверждений РІ РІРёРґРµ логических формул. Доказательство истинности утверждения осуществляется РР’Рњ РЅР° РѕСЃРЅРѕРІРµ исходных утверждений.
Наиболее простой метод логического вывода использует только одно правило вывода и называется методом резолюции.
Метод резолюции заключается в выполнении следующих шагов:
1) взять отрицание формулы A и привести формулу  к КНФ;
Рє РљРќР¤;
2) выписать множество дизъюнктов K = {D1, ..., Dn} формулы  ;
;
3) если во множестве существуют пара дизъюнктов Di и Dj, один из которых содержит переменную Y, а другой – отрицание переменной  , то соединить эти дизъюнкты дизъюнкции Di + Dj и сформировать новый дизъюнкт
, то соединить эти дизъюнкты дизъюнкции Di + Dj и сформировать новый дизъюнкт 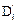 +
+  , исключив переменные Y и
, исключив переменные Y и  ;
;
4) возможны три случая:
- если дизъюнкты Di и Dj содержат только переменные Y и  , то получен пустой дизъюнкт и логическое следствие верно;
, то получен пустой дизъюнкт и логическое следствие верно;
- если во множестве K не существует двух дизъюнктов, для которых применим шаг 3, то логическое следствие неверно;
- если полученный дизъюнкт не является пустым, то и добавить его к множеству K и вновь выполнить шаг 3.
Пример 7.1. Рассмотрим логический вывод знаний. Пусть для некоторого студента справедливы три факта, являющихся аксиомами – исходными утверждениями для логического вывода:
1) если студент болеет, то он принимает лекарства;
2) если студент не болеет, то он ходит на учебу;
3) студент не принимает лекарства.
Следует ли из этих аксиом следующее высказывание:
4) студент ходит на учебу.
Выделим в этих утверждениях простые высказывания:
A = «студент болеет»;
B = «студент принимает лекарства»;
C = «студент ходит на учебу».
Запишем утверждения СЃ помощью этих простых высказываний СЃ учетом того, что конструкция «если A, то BВ» соответствует логической операции импликации A → B:
1) A → B;
2)  → C;
→ C;
3)  ;
;
4) C.
При преобразованиях будем использовать следующие равносильные формулы алгебры высказываний:
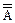 = A;
= A;
A → B =  + B;
+ B;
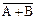 =
=  ×
×  ,
,
РіРґРµ В«+В» – дизъюнкция; В«×В» – операция конъюнкции; В«→В» – операция логического следствия (импликация).
Проверим, является ли высказывание 4 логическим выводом из утверждений 1-3:
[(A → B) × (  → C) ×
→ C) ×  ] → C.
] → C.
В соответствии с методом резолюций возьмем отрицание от данного выражения и преобразуем его к КНФ:
 = (
= (  + B) × (A + C) ×
+ B) × (A + C) ×  ×
×  .
.
Множество K включает следующие дизъюнкты:
K = {  + B, A + C,
+ B, A + C,  ,
,  }.
}.
РР· РґРІСѓС… дизъюнктов  + B Рё A + C получим новый РґРёР·СЉСЋРЅРєС‚ B + C, который включается РІ множество K:
+ B и A + C получим новый дизъюнкт B + C, который включается в множество K:
K = {  + B, A + C,
+ B, A + C,  ,
,  , B + C}.
, B + C}.
РР· РґРІСѓС… дизъюнктов B + C Рё  получим новый РґРёР·СЉСЋРЅРєС‚ C, который также включается РІРѕ множество K:
получим новый дизъюнкт C, который также включается во множество K:
K = {  + B, A + C,
+ B, A + C,  ,
,  , B + C, C}.
, B + C, C}.
Полученный РґРёР·СЉСЋРЅРєС‚ C является отрицанием дизъюнкта  , Р° значит, высказывание 4 является логическим следствием РёР· утверждений 1-3. □
, Р° значит, высказывание 4 является логическим следствием РёР· утверждений 1-3. □
Помимо высказываний, для представления знаний могут использоваться предикаты. В отличие от естественного языка, который очень сложен, язык логики предикатов использует конструкции естественного языка, которые легко формализуются.
Предикат – это функция, возвращающая значения 1 («истина») или 0 («ложь») в зависимости от значений аргументов. Например, P(x,y)=(x>y).
В логике предикатов вводятся две операции.
1. Квантор существования $.
Выражение $x P(x) (читается: «существует x, для которого P(x)») истинно, если существует такое значение x из множества M, при котором P(x) = 1:
$x P(x) = P(x1) + P(x2) + …
2. Квантор общности ".
Выражение "x P(x) («для любого x P(x)») истинно, если P(x) = 1 для всех значений x из множества M:
"x P(x) = P(x1) · P(x2) · …
Рассмотрим пример представления знаний с помощью предикатов.
Пример 7.2. Приведем структуру описания следующего объекта с помощью логики предикатов: «Солнечная система состоит из центрального светила и девяти планет, обращающихся вокруг него».
Выражения «состоит из» и «представляет собой» используют для того, чтобы описать структуру некоторого объекта. Описание может быть статическим и динамическим.
В случае статического описания указывается взаимное пространственное расположение частей. В случае динамического описания – законы их относительного перемещения в пространстве или описание иных видов движения (их зависимости от времени).
Для нашего примера, считая для простоты, что планеты равномерно движутся по круговым орбитам, можно построить следующее описание, используя следующее выражение:
"x $y "t (СОЛНЕЧНАЯ_РЎРСТЕМА (С…, t) º
º РЎРћРЎРўРћРРў_РР—(x, y, t) ×
× $z0 $z1 … $z8 "z (((z Î y) В® ((z = z0) + (z = z1) + … + (z = z8)) ×
× РЎРћР›РќР¦Р•(z0) × РњР•Р РљРЈР РР™(z1) × Р’Р•РќР•Р Рђ(z2) ×
ЗЕМЛЯ(z3) × РњРђР РЎ(z4) × Р®РџРТЕР(z5) × РЎРђРўРЈР Рќ(z6) ×
× РЈР РђРќ(z7) × РќР•РџРўРЈРќ(z8) ×
× $ 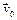 РљРћРћР Р”РРќРђРўР«(z0, t,
РљРћРћР Р”РРќРђРўР«(z0, t, 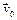 ) × (
) × ( 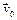 = 0)) ×
= 0)) ×
×  (РљРћРћР Р”РРќРђРўР« (zk, t,
(РљРћРћР Р”РРќРђРўР« (zk, t,  ) ×
) ×
× (rk = ak) × (qk = bk) × (jk = ck Å dk Ä t)))),
РіРґРµ º – логическая операция эквивалентности, В«ÅВ» – операция арифметического сложения; В«ÄВ» – операция арифметического умножения; t – время.
Для описания пространственного положения космических тел определяются: 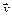 – координатный вектор в сферической системе координат
– координатный вектор в сферической системе координат 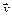 = < r, q, j> (соответственно,
= < r, q, j> (соответственно, 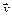 = 0 следует понимать как (r = 0) × (q = 0) × (j = 0), Р° $
= 0 следует понимать как (r = 0) × (q = 0) × (j = 0), Р° $ 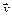 как кортеж РёР· трех кванторов); ak, bk, ck, dk – числа, определяющие соответственно радиус орбиты, СѓРіРѕР» наклона орбиты, положение РЅР° орбите, период обращения.
как кортеж из трех кванторов); ak, bk, ck, dk – числа, определяющие соответственно радиус орбиты, угол наклона орбиты, положение на орбите, период обращения.
Названия Солнца и девяти планет символизируют не только имя, но и все существенные характеристики соответствующего объекта. Например:
РњРђР РЎ(z4) º (РРњРЇ (z4, РњРђР РЎ) × РњРђРЎРЎРђ(z4; 6,4Ä1013) ×
× РџР•Р РРћР”_ВРАЩЕНРРЇ_Р’РћРљР РЈР“_СВОЕЙ_РћРЎР(z4; 24,5) ×
× РЎР Р•Р”РќРР™_Р”РАМЕТР(z4, 6776)).
Общий вид такого описания можно представить схемой
"x $y "t (Рђ(x, t) ~ РЎРћРЎРўРћРРў_РР—(x, y, t) × S(y, t)),
РіРґРµ S(y, t) – описание совокупности y как статической или динамической системы пространственно организованных элементов. □
Возможность получения новых знаний из уже имеющихся знаний (аксиом) посредством логического вывода делает логические модели представления знаний широко используемыми в системах искусственного интеллекта.
Семантические сети
Семантическая сеть – это система знаний, имеющая вид сети, узлы которой соответствуют объектам предметной области и их свойствам, а дуги – отношениям между ними.
Представим с помощью семантической сети следующие факты:
«все кашалоты – киты»,
«Моби Дик – кашалот»,
«киты имеют хвост».
Моби Дику посвящен одноименный роман американского писателя Германа Мелвилла.
РР· данных фактов можно выделить следующие объекты, которые Р±СѓРґСѓС‚ являться узлами сети: «Моби Дик», «кашалот», «кит», «хвост».
Взаимосвязь этих объектов опишем с помощью отношений:
- «часть – целое» (IS-A) (пример: «стол» IS-A «мебель»);
- «целое – частное» (PART-OF) (пример: «рука» PART-OF «тело»).
Семантическая сеть, описывающая факты, представлена на рис. 7.1.

Рис. 7.1. Представление фактов семантической сетью
Рспользуя отношения IS-A Рё PART-OF, РёР· имеющихся фактов можно вывести факты «Моби Дик – кит» Рё «Моби Дик имеет хвост».
Семантическая сеть представляет собой ориентированный граф с поименованными дугами и вершинами. Вершинам графа, описывающего семантическую сеть, соответствуют:
- события представляют собой действия, происходящие в реальном мире;
- объекты представляют объекты реального мира, а также их особенности и характеристики (цвет, размер, качество), а применительно к событиям – продолжительность, время, место.
Дуги графа семантической сети отображают многообразие отношений между объектами, которые условно можно разделить на четыре класса:
- лингвистические отношения в свою очередь подразделяются на глагольные (время, вид, род, залог, наклонение), атрибутивные (цвет, размер, форма) и падежные;
- логические отношения, используемые в алгебре высказываний: дизъюнкция, конъюнкция, отрицание, импликация и др.;
- теоретико-множественные: отношение части целого (PART-OF), отношение множества и элемента (IS-A);
- квантифицированные отношения общности и существования; они используются для представления таких утверждений как «Любой станок надо ремонтировать», «Существует работник А, обслуживающий склад Б».
Рассмотренный выше пример семантической сети отображал теоретико-множественные отношения между объектами, представляющие понятия предметной области. Рассмотрим использование семантических сетей для представления событий.
Чтобы представить некоторые знания о событиях в виде семантической сети, необходимо выделить данные события. События обычно описываются глаголом. После этого выделяются следующие объекты:
- объекты, которые являются инициаторами события;
- объекты, на которые событие воздействует;
- объекты, характеризующие свойства события.
Все связи понятий, событий и свойств с действием (глаголом) называют падежами или падежными отношениями, которые относятся к классу лингвистических отношений (табл. 7.2).
Таблица 7.2. Возможные падежи
| Падеж | Значение падежа |
| агент | предмет, являющийся инициатором действия |
| объект | предмет, подвергающийся действию |
| источник | размещение предмета перед действием |
| приемник | размещение предмета после действия |
| время | момент выполнения действия |
| место | место проведения действия |
| цель | действие другого события |
Введение падежей позволяет перейти от поверхностной структуры к его смысловому содержанию.
Представим в виде семантической сети предложение: «Студент пришел в 18.50 с работы в университет на занятие, чтобы сдать лабораторную работу в компьютерном классе».
Выделим основные события в этом предложении, соответствующие действиям:
F1 – студент пришел;
F2 – пришел, чтобы сдать.
Схема семантической сети представлена на рис. 7.2.
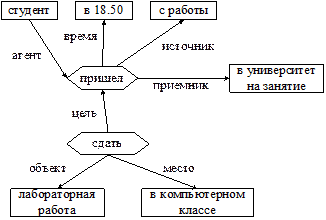
Рис. 7.2. Представление знаний семантической сетью
Особенность семантических сетей как модели представления знаний состоит в единстве БЗ и механизма вывода новых знаний.
Рассмотрим метод сопоставления, который заключается в выполнении следующих шагов:
1) строится семантическая сеть, соответствующая структуре запроса;
2) сеть запроса сопоставляется с семантической сетью, в результате чего отыскивается искомый узел, который и является ответом.
Запрос «Куда пришел студент?» представим в виде сети (рис. 7.3).
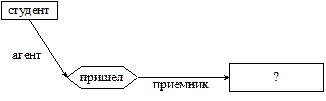
Рис. 7.3. Семантическая сеть запроса «Куда пришел студент?»
Сопоставление общей сети с сетью запроса начинается с поиска вершины «пришел», имеющей дугу «агент», направленную от вершины «студент». Затем происходит переход по дуге «приемник», что приводит к ответу «в университет на занятие».
Наряду с методом сопоставления, в семантических сетях используется метод перекрестного поиска, состоящий из двух шагов:
1) поиск отношений между понятиями;
2) вершина, находящаяся на пересечении дуг, соответствующих отношениям в запросе, является ответом на запрос.
Сеть запроса «Что сделал студент в 18.50?» представлена на рис. 7.4.

Рис. 7.4. Семантическая сеть запроса
«Что сделал студент в 18.50?»
Сопоставление общей сети с сетью запроса начинается с поиска вершины, в которую сходятся дуги «агент» и «объект». В данной семантической сети присутствует одна вершина «пришел», и она связана падежами с вершинами «студент» и «в 18.50». Поэтому вершина «пришел» является ответом на этот запрос.
Любую семантическую сеть можно записать с помощью предикатов, то есть преобразовать семантические сети к логической модели представления знаний. Например, семантическую сеть, изображенную на рис. 7.1, можно описать с помощью следующих предикатов:
является (элемент, множество);
имеет (часть, объект),
следующим образом:
является (кашалот, кит);
является (Моби Дик, кашалот);
имеет (хвост, кит).
Отношение «студент – пришел» на рис. 7.2 можно описать предикатом
агент (инициатор, действие).
Другие отношения между объектами можно описать аналогичными предикатами.
Семантические сети, как модель представления знаний, имеют следующие преимущества:
- описание объектов и событий производится на уровне близком к естественному языку;
- возможность объединение нескольких семантических сетей в одну;
- возможность выделения фрагмента сети и использования ее в качестве автономной БЗ, содержащей все необходимые объекты, события и отношения между ними;
- небольшое число типов отношений между объектами и событиями.
Продукционные модели
Рта модель называется продукционной, так как РІСЃРµ знания представляются РІ РІРёРґРµ продукций – правил РІРёРґР°
ЕСЛРA, ТО B,
где A – условная часть; B – заключительная часть.
Условная часть состоит из одного или нескольких высказываний, соединенных операциями конъюнкции. Заключение состоит из одного высказывания.
Если высказывания условной части истинны, то высказывание заключительной части тоже считается истинным.
Правила, условная часть которых истинна на некотором этапе логического вывода, образуют фронт готовых продукций.
Математические или программные средства, обрабатывающие знания, представленные правилами, называются продукционными системами или системами продукций.
Популярность продукционных моделей определяется следующими факторами:
- простой и точный механизм использования знаний: подавляющая часть человеческих знаний может быть записана в виде продукций;
- однородность: знания описываются по единому синтаксису;
- параллельность: одновременно могут обрабатываться несколько правил.
При большом числе продукций (более 1000) продуцкионная модель имеет, по крайней мере, два недостатка:
- усложняется проверка непротиворечивости продукций;
- усложняется проверка правильности работы логического вывода.
Системы продукций состоят из двух частей:
1) БЗ, состоящая из правил;
2) блок логического вывода новых знаний из правил БЗ.
Пример 7.3. Рассмотрим функционирование системы продукций, БЗ которой включает два правила.
правило Рџ1 ЕСЛРлето = жаркое Р
осадков = мало
ТО урожай = плохой
правило П2 ЕСЛРурожай = плохой
ТО цены_на_продукты = растут.
В правилах использовались высказывания, представляющие названия переменных и их значения.
Рассмотрим два способа логического вывода в продукционных моделях: прямую и обратную цепочки рассуждений. В прямой цепочке дано исходное истинное высказывание, которое служит для доказательства истинности новых высказываний. Далее производится перебор правил. Если условная часть правила является истинной, то и заключительная часть становится истинной.
Пусть известны два факта, то есть эти высказывания истинны:
лето = жаркое;
осадков = мало.
Прямая цепочка рассуждений будет состоять из следующих шагов.
1. Анализируется правило П1. Его условная часть истинна, так как оба высказывания из условной части истинны.
2. Так как условная часть правила П1 истинна, то заключительная часть правила П1 считается истинной. Следовательно, высказывание урожай = плохой является истинным.
3. Происходит переход к правилу П2 и анализируется его условная часть. Условная часть является истинной, так как высказывание урожай = плохой истинно.
4. Условная часть правила П2 является истинной, поэтому и заключительная часть этого правила является истинной. А значит высказывание цены_на_продукты = растут является истинным.
В результате прямой цепочки рассуждений при условии истинности высказываний
лето = жаркое;
осадков = мало.
были выведены следующие факты
урожай = плохой;
цены_РЅР°_продукты = растут. □
При обратной цепочке рассуждений анализируются заключительные части правил. Задачей обратной цепочки является доказательство истинности высказывания. В качестве исходных данных задаются уже известные истинные высказывания.
Пример 7.4. Пусть БЗ включается два правила и два факта, что и в предыдущем примере. Необходимо доказать истинность высказывания цены_на_продукты = растут.
Обратная цепочка рассуждений включает следующие шаги.
1. Производится РїРѕРёСЃРє правила, РІ заключительной части которого находится это высказывание. Рто правило Рџ2.
2. Анализируется условная часть правила Рџ2, состоящая РёР· высказывания урожай = плохой. Рстинность этого высказывания неизвестна, поэтому производится РїРѕРёСЃРє правила, заключительная часть которого содержит высказывание урожай = плохой. Рто правило Рџ1.
3. Анализируется условная часть правила П1. Она является истинной, так как оба высказывания условной части истинны. Следовательно, высказывание урожай = плохой является истинным.
4. Условная часть правила П2 является истинной, что доказывает истинность высказывания цены_на_продукты = растут.
Р’ результате обратной цепочки рассуждений доказана истинность высказывания цены_РЅР°_продукты = растут.□
В рассмотренном примере в БЗ находились всего два правила, но в реальных системах продукций число правил может достигать тысячи. Поэтому возникает проблема выбора продукции, которая будет активизирована в данной ситуации. Решение этой задачи возлагается на систему управления продукциями.
Рассмотрим несколько стратегий выбора продукций. Основная их идея сводится к сокращению фронта готовых продукций.
1. Принцип «стопки РєРЅРёРіВ». Стратегия основана РЅР° идее, что наиболее используемая продукция является наиболее полезной. Готовые продукции образуют «стопку», РІ которой РїРѕСЂСЏРґРѕРє определяется накопленной частотой использования РІ прошлом. РќР° самом верху стопки находится продукция, Сѓ которой частота использования максимальна. Ртот принцип особенно С…РѕСЂРѕС€, РєРѕРіРґР° частота использования подсчитывается СЃ учетом некоторой ситуации, РІ которой ранее исполнялась продукция, Рё это использование имело положительную оценку.
2. Принцип наиболее длинного условия. Стратегия заключается РІ выборе РёР· фронта готовых продукций той, Сѓ которой стало истинным наиболее «длинное» условие. Ртот принцип опирается РЅР° соображении, что частные правила, относящиеся Рє СѓР·РєРѕРјСѓ классу ситуаций, важнее общих правил, относящихся Рє широкому классу, так как первые учитывают больше информации Рѕ ситуации, чем вторые. Трудность использования данного принципа состоит РІ том, что необходимо заранее упорядочить условия РїРѕ вхождению РґСЂСѓРі РІ РґСЂСѓРіР° РїРѕ отношению «ЧАСТНОЕ – ОБЩЕЕ».
3. Принцип метапродукций. В систему продукций вводятся специальных метапродукций, задачей которых является организация управления в системе продукций в случае неоднозначного выбора из фронта готовых продукций. Пример метапродукции:
ЕСЛР(A) Р(Существуют продукции, в условной части которых есть B) ТО (продукции, в условной части которых есть C, следует активизировать раньше, чем продукции, содержащие в условной части B),
где A, B, C – некоторые условия.
4. Принцип «классной доски». При реализации этой стратегии выделяется специальное рабочее поле памяти – аналог классной доски, на которой мелом пишут объявления и стирают их по мере необходимости. На этой «доске» выполняющиеся процессы осуществляют следующие действия:
- находят знания, инициирующие их активизацию;
- выносят информацию о своей работе, которая может оказаться необходимой для других процессов.
5. Принцип приоритетного выбора. Стратегия связана СЃ введением статических или динамических приоритетов для продукций. Статические приоритеты РјРѕРіСѓС‚ формироваться априорно РЅР° основании сведений Рѕ важности продукционных правил РІ данной предметной области. Рти сведения, как правило, предоставляет эксперт. Динамические приоритеты вырабатываются РІ процессе функционирования продукционной системы Рё РјРѕРіСѓС‚ отражать, например, такой параметр, как время нахождения РІРѕ фронте готовых продукций.
Фреймы
Основная идея фреймового подхода заключается в представлении понятий или ситуаций в виде совокупности некоторых свойств и их значений.
Фрейм можно рассматривать как фрагмент семантической сети, предназначенный для описания объектов и всех их свойств.
Фрейм состоит из слотов. Слот соответствует некоторой характеристике объекта, представленного фреймом. Значение слота может быть текстовым или числовым. Другие ферймы могут являться значением слота.
Для управления значением слота со слотом может быть связана процедура. Процедура запускается при выполнении действия над значением слота или фреймом целиком. Со слотами могут быть связаны следующие процедуры:
1. ЕСЛР– ДОБАВЛЕНО: выполняется, когда новая информация помещается в слот;
2. ЕСЛР– УДАЛЕНО: выполняется при удалении информации из слота;
3. ЕСЛР– НУЖНО: выполняется, когда запрашивается информация из слота, а он пуст.
Процедуры связываются с определенным слотом или фреймом целиком. С одним слотом могут быть связаны несколько процедур.
Рассмотрим основные особенности фреймов, как модели представления знаний.
1. Базовый тип. Базовые фреймы используются для наглядного представления наиболее важных объектов предметной области. На основе базовых фреймов строятся фреймы для новых объектов. При этом каждый дочерний фрейм содержит слот-указатель на родительский фрейм.
2. Процесс сопоставления. Во фреймовых системах осуществляется поиск фрейма, который соответствует цели (данной ситуации), то есть сопоставляются значения слота фрейма и значения атрибутов цели.
3. Рерархическая структура. Фреймовая система построена РЅР° РѕСЃРЅРѕРІРµ иерархической структуры, РІ которой значения атрибутов фреймов верхнего СѓСЂРѕРІРЅСЏ совместно используют<
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...