
Главная Случайная страница
Категории:
ДомЗдоровьеЗоологияРнформатикаРскусствоРскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиРкологияРРєРѕРЅРѕРјРёРєР°Рлектроника
Логические функции Microsoft Excel
В табличном процессоре Microsoft Excel существуют следующие элементы логики высказываний:
- логические константы ЛОЖЬ Рё РРЎРўРРќРђ, вместо которых можно использовать 0 Рё 1 соответственно;
- логические функции, возвращающие в качестве результата одну из логических констант:
1) отрицание: НЕ(x);
2) конъюнкция: Р(x1[; x2; …; x30]);
3) дизъюнкция: РР›Р(x1[; x2; …; x30]).
Р’ функциях Р Рё РЛРможно использовать РѕС‚ 1 РґРѕ 30 аргументов. Р’ качестве аргументов РјРѕРіСѓС‚ выступать логические константы, логические условия (например, 2 + 2 > 4) или ссылки РЅР° ячейки, РіРґРµ содержатся логические константы или значения.
Если в ячейках не содержатся логические значения, то логические функции возвращают значение ошибки #ЗНАЧ!.
Пример. Записать в виде формулы функцию
y = 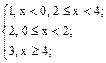 .
.
Запишем условия первых и вторых случаев в виде простых условий:
1) (x < 0) или ((x ³ 2) Рё (x < 4));
2) (x ³ 0) Рё (x < 2);
3) x ³ 4.
Запишем условия первого случая в виде формулы, значение x находится в ячейке A1:
=РР›Р(A1<0;Р(A1>=2;A1<4)).
Запишем формулу для функции:
=ЕСЛР(РР›Р(A1<0;Р(A1>=2;A1<4));1;ЕСЛР(Р(A1>=0;A1<2);2;3)).
10.6.7. Функции теории вероятностей
и математической статистики в Microsoft Excel
Выборочные характеристики
Дисперсия выборки из генеральной совокупности:
Р”РРЎРџ(x1; x2; …; x30).
Формула вычисления выборочной дисперсии:
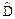 =
= 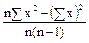 .
.
Дисперсия генеральной совокупности:
Р”РРЎРџР Рђ(x1; x2; …; x30).
Р’ отличие РѕС‚ функции Р”РРЎРџ РїСЂРё вычислении значения функции Р”РРЎРџР Рђ предполагается, что РІ параметрах функции представлена РІСЃСЏ генеральная совокупность, Р° РЅРµ выборка РёР· нее.
Формула вычисления дисперсии генеральной совокупности:
D = 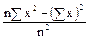 .
.
Медиана – это число, которое является серединой упорядоченной последовательности чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел – меньшие, чем медиана:
МЕДРРђРќРђ(x1; x2; …; x30).
Если количество значений четное, то функция вычисляет среднее двух значений, находящихся в середине последовательности.
Мода – это наиболее часто встречающееся или повторяющееся значение в последовательности чисел:
МОДА(x1; x2; …; x30).
Если несколько значений встречаются одинаковое количество раз, то возвращается минимальное значение.
Наименьшее k-е значение из значений диапазона ячеек:
РќРђРМЕНЬШРР™(диапазон; k).
Рта функция используется для определения значения, занимающего определенное относительное положение среди значений диапазона ячеек.
Минимальное значение последовательности имеет k = 1.
Если диапазон РїСѓСЃС‚ или k ≤ 0 или k превышает число ячеек диапазона, то функция возвращает значение ошибки #Р§РСЛО!.
Наибольшее k-е из значений диапазона ячеек:
РќРђРБОЛЬШРР™(диапазон; k).
Среднее арифметическое:
СРЗНАЧ(x1; x2; …; x30),
где x1; x2; …; x30 – числа, имена или ссылки, содержащие числа.
Ячейки, не содержащие числа, игнорируются.
Формула вычисления среднего арифметического:
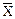 =
= 
Среднее гармоническое:
СРГАРМ(x1; x2; …; x30).
Если РѕРґРёРЅ РёР· аргументов функции отрицательный, то функция СРГАРМ возвращает значение ошибки #Р§РСЛО!.
Формула вычисления среднего гармонического:
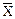 гарм. =
гарм. = 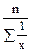 .
.
Среднее геометрическое:
СРГЕОМ(x1; x2; …; x30).
Формула вычисления среднего геометрического:
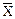 геом. =
геом. =  .
.
Среднее доли множества данных, отбрасывая числа с экстремальными значениями:
УРЕЗСРЕДНЕЕ(диапазон; доля),
где диапазон – интервал усредняемых значений; доля – процент значений, исключаемых из вычислений.
Например, если доля = 0,2, то отбрасываются 10% чисел с наибольшими значениями и 10% чисел с наименьшими значениями.
Значение параметра доля лежит РІ диапазоне [0; 1], иначе функция возвращает значение ошибки #Р§РСЛО!.
УРЕЗСРЕДНЕЕ округляет в меньшую сторону количество отбрасываемых значений до ближайшего четного целого.
Комбинаторика
Количество размещений из n элементов по m – любых упорядоченных множеств из m элементов множества, состоящего из n различных элементов:
ПЕРЕСТ(n; m).
Оба аргумента усекаются до целых.
Если n или m не является числами, то функция возвращает значение ошибки #ЗНАЧ!.
Если n ≤ 0 или m < 0 или n < m, то функция ПЕРЕСТ возвращает значение ошибки #Р§РСЛО!.
Формула расчета размещений:
 =
= 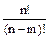 .
.
Количество сочетаний из n элементов по m – размещений, в которых не учитывается порядок элементов:
Р§РСЛКОМБ(n; m).
Формула расчета сочетаний:
 =
= 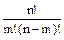 .
.
Законы распределения
Значение биномиального распределения (распределения Бернулли, формулы Бернулли):
Р‘РРќРћРњР РђРЎРџ(k; n; p; признак),
где k – количество успешных испытаний; n – число независимых испытаний; p – вероятность успеха в каждом испытании; признак – логическое значение, определяющее форму функции.
Если параметр признак имеет значение РРЎРўРРќРђ, то функция возвращает интегральную функцию распределения, то есть вероятность того, что число успешных испытаний РЅРµ более значения параметра k. Если этот параметр имеет значение ЛОЖЬ, то возвращается функция распределения, то есть вероятность того, что число успешных испытаний РІ точности равно значению параметра k.
Параметры k и n усекаются до целых.
Функция возвращает значение ошибки #ЗНАЧ!, если k, n или p не является числом.
Функция возвращает значение ошибки #Р§РСЛО! РІ следующих случаях:
1) k < 0 или k > n;
2) p < 0 или p > 1.
Формула расчета значения интегрального биномиального распределения:
Pn(x ≤ k) = 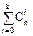 pi(1 – p)n–i.
pi(1 – p)n–i.
Формула расчета значения биномиального распределения:
Pn(x = k) = 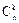 pk(1 – p)n–k.
pk(1 – p)n–k.
Значение гипергеометрического распределения:
Р“РПЕРГЕОМЕТ(m; n; M; N),
где m – число успехов в выборке; n – размер выборки; M – число успехов в генеральной совокупности; N – размер генеральной совокупности.
Все аргументы усекаются до целых.
Если любой из аргументов не является числом, то функция возвращает значение ошибки #ЗНАЧ!.
Функция возвращает значение ошибки #Р§РСЛО! РІ следующих случаях:
1) m < 0 или m > min{n, M};
2) m < min{0; n – N + M};
3) n < 0 или n > N;
4) M < 0 или M > N;
5) N < 0.
Формула расчета значения гипергеометрического распределения:
P = 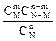 .
.
Значение функции нормального распределения для указанного среднего и стандартного отклонения:
НОРМРАСП(x; a; s; признак),
где x – значение, для которого строится распределение; a – математическое ожидание нормального распределения; s – среднее квадратическое отклонение; признак – логическое значение, определяющее форму функции.
Если параметр признак имеет значение РРЎРўРРќРђ, то функция возвращает интегральную функцию распределения. Если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.
Функция возвращает значение ошибки #ЗНАЧ!, если a или s не является числом.
Функция возвращает значение ошибки #Р§РСЛО!, если s ≤ 0.
Формула интегральной функции нормального распределения:
F(x) = 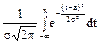 .
.
Формула плотности нормального распределения:
f(x) = 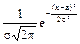 ,
,
Если a = 0, s = 1 Рё признак = РРЎРўРРќРђ, то функция РќРћР РњР РђРЎРџ возвращает стандартное нормальное распределение, то есть РќРћР РњРЎРўР РђРЎРџ:
РќРћР РњРЎРўР РђРЎРџ(x),
где x – значение, для которого строится распределение.
Формула плотности стандартного нормального распределения:
j(x) =  .
.
Значение распределения Пуассона:
ПУАССОН(k; l; признак),
где k – количество событий; l – среднее количество событий в единицу времени; признак – логическое значение, определяющее форму возвращаемого распределения вероятностей.
Если параметр признак имеет значение РРЎРўРРќРђ, то функция возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий будет РѕС‚ 0 РґРѕ k включительно. Если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения Пуассона, то есть вероятность того, что число событий равно k.
Параметр k усекается до целого.
Функция возвращает значение ошибки #ЗНАЧ!, если k или l не является числом.
Функция возвращает значение ошибки #Р§РСЛО! РІ следующих случаях:
1) k ≤ 0;
2) l ≤ 0.
Формула расчета интегрального распределения Пуассона:
Pn(x £ k) =  .
.
Функция плотности распределения Пуассона:
Pn(x = k) = 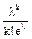 .
.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...