Розсіювання на потенційному бар'єрі

Зміст

Вступ............................................................................................................................................... 4

1. Елементи квантової механіки................................................................................ 5

1.1. Світло. Квантування.......................................................................................................... 6

1.2. Хвильова функція................................................................................................................ 7

1.3. Рівняння Шредінгера.......................................................................................................... 9

1.4. Стан однієї частинки........................................................................................................ 11

1.5. Розсіювання на потенційному бар'єрі.......................................................................... 17

2. Електронна провідність наноструктур.......................................................... 19

2.1. Модель Друде. Класична модель електронної провідності..................................... 20

2.2. Квантова модель вільних електронів........................................................................... 22

2.3. Режими переносу заряду в наноструктурах................................................................ 29

2.4. Опір балістичного провідника........................................................................................ 30

2.5. Квантовий крапковий контакт....................................................................................... 39

2.6. Опір нанопровідника. Формула Ландауера................................................................. 41

2.7. Нанопровідник з багатьма домішками....................................................................... 45

Висновок.................................................................................................................................... 48

Рекомендована література.......................................................................................... 50

Вступ

Сучасна технологія відрізняється упором на мініатюризацію. Мабуть, самим яскравим прикладом є електроніка, де чудовий технічний прогрес насамперед пов'язаний зі скороченням розмірів транзисторів, що приводить до можливості збільшення числа транзисторів на інтегральній мікросхемі. Чим більше транзисторів на чипі, тим більше складні інтегральні схеми. За останні 35 років інженери збільшили складність інтегральних схем більш ніж на п'ять порядків. Це чудове досягнення змінило сучасне суспільство. Зокрема, найчастіше різноманітні механічні пристрої мають половину своєї вартості саме в електроніці. †

Тенденції в електроніці до стійкого росту складності відзначив Гордон Мур, один із засновників корпорації Intel. Однойменний закон Мура говорить, що складність інтегральних схем, стосовно мінімальної вартості компонентів, подвоюється приблизно через 18 місяців. Як видно з малюнка 1(а), згодом «закон» Мура виявила себе дуже добре.

Тенденція до мініатюризації приводить до зменшення розмірів транзисторів і провідників, вивчення й розрахунок яких вимагає залучення більше просунутих теоретичних концепцій. Оскільки розмір сучасних електронних компонентів виходить на нанорівень (1нм= 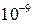м), стає важливим облік хвильових властивостей окремих носіїв заряду, що призводить до більш широкого застосування методів квантової механіки. Отже, наноэлектроніка - електроніка на наномасштабах.

У даному посібнику викладено базові відомості, що стосуються методів розрахунку наноструктур. Основну увагу зосереджено на розгляді електричної провідності. Оскільки тут вже працює квантова механіка, яка стає робочим інструментом сучасного інженера, ми виклали ряд її основних положень.

Рис. 1(а). Кількість транзисторів у процесорах фірми INTEL як функція часу

Елементи квантової механіки

У введенні було зазначено, що розмір сучасних електронних пристроїв виходить на нанорівень. Так деякі процесори виготовлені по 20 нм технології й менш. Це не означає, що, наприклад, такий розмір має кожний структурний елемент схеми. Отут скоріше говориться про масштаби провідників і контактів. Проте, якщо говорити про подібні масштаби, то для опису виникаючих явищ необхідно керуватися іншими правилами, ніж закони класичної фізики. Тут уже працює квантова механіка. Квантова механіка - фундаментальна наука, що вивчає властивості дрібних часток речовини. Її закони описують поводження електронів, атомів або молекул і здаються досить дивними, непоясненими з погляду здорового глузду. Те, що справедливо у світі звичайних тіл, з якими ми маємо справу в техніку або повсякденному житті, нерідко виявляється невірним у світі атомів.

Донедавна інженери - розроблювачі електронних приладів - у своїх розрахунках використовували тільки закони класичної фізики. І це було цілком виправдано, оскільки, наприклад, у звичайному кінескопі телевізора електрони рухаються так само, як класичні матеріальні крапки - биліардные кулі або м'ячі. У сучасному мікропроцесорі комп'ютера рух мікроскопічних електронів також подібно руху класичних тел. Однак ситуація міняється. Логіка розвитку сучасної напівпровідникової електроніки така, що інтегральні схеми стають усе більше складними й поєднують все більше число елементів. Дотепер виготовлювачам інтегральних схем вдавалося збільшувати щільність розміщення транзисторів, діодів і інших елементів за рахунок зменшення їхніх розмірів. Імовірно, що в недалекому майбутньому ці розміри стануть порядку декількох часток мікрона. У той момент, коли це відбудеться, опис мовою класичної фізики втратить усякий зміст і творці електронних приладів будуть змушені звернутися до квантової механіки.

Не чекаючи цього моменту, фізики вже нагромадили великий досвід у розробці приладів, дія яких засноване на квантовомеханічних принципах. Укладаючи атоми з точністю до одного-двох шарів, вони можуть створювати штучні кристали, молекули й навіть атоми із заданими властивостями. Такі напівпровідникові структури мають розміри в кілька нанометрів або кілька десятків ангстрем. Хоча зазначені розміри ще перевищують розміри справжніх атомів, електрони в цих структурах поводяться як квантові об'єкти. Можна виділити три основних типи мікроструктур: квантові ями, нитки й крапки, причому останні іноді називають штучними атомами. Вивчення цих структур не тільки відкриває нові сторінки електронної інженерії, але й супроводжується відкриттями фундаментального характеру.

Світло. Квантування

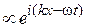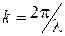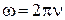Світло – електромагнітна хвиля. Напруженість електричного поля хвилі, яка розповсюджується , де - хвильове число, - довжина хвилі, - частота ( =Гц ), , - швидкість світла. Насправді, хвильове число – векторна величина, що показує напрямок поширення хвилі. Знайдемо швидкість хвилі. Для цього фіксуємо крапку постійної фази 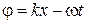й будемо стежити за її переміщенням. За час 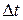ця крапка перемістилася на відстань 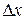, при цьому, у силу умови сталості фази, . Таким чином, 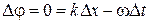або 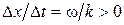- фазова швидкість хвилі. Як легко переконатися, для електромагнітної хвилі швидкість дорівнює швидкості світла. Хвиля поширяться праворуч, оскільки 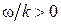. З іншого боку, хвиля 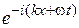- ліворуч.

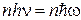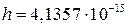У квантовій механіці енергія електромагнітної хвилі приймає ряд дискретних значень , - кількість квантів, eB 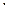c – постійна Планка ( 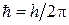). Квант електромагнітного поля (фотон) має енергію 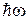й імпульс 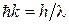. Звичайно вважається, що в елементарних процесах число квантів змінюється на 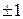. Наприклад, електрон в атомі переходить із більше високого рівня з енергією 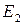на більше низький 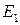, народжується один фотон 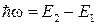. Далі, використовуючи аналогію з картиною квантування світла, перейдемо до опису квантового миру матеріальних часток.

Хвильова функція

При проходженні світла через дві щілини, які вирізано в площині, на екрані спостерігається картина із темних та світлих смуг, що виникають через інтерференцію двох хвильових пучків. Як виявилося, така ж картина буде спостерігатися при розсіюванні електронів на двох щілинах (див. Рис. 1.).

Таким чином, електрони демонструють, поряд з корпускулярними, хвильові властивості. Це так званий «корпускулярно-хвильовий дуалізм». Для опису хвильових властивостей електронів необхідно ввести підходящий математичний апарат - квантову механіку.

Рис 1. Розподіл електронів залежно від їхньої кількості при проходженні через дві вертикальні щілини.

Дотримуючись законів квантової механіки, уведемо хвильову функцію - 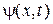. Це комплексна функція, причому квадрат модуля 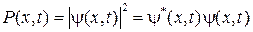- є щільність імовірності розподілу електронів у крапці 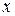в момент часу . Якщо хвильова функція описує один електрон, імовірність знаходження електрона в системі буде дорівнює одиниці. Звідси витікає умова нормування

. (1)

Далі, природно припустити, що хвильова функція 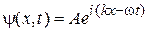описує електрон з енергією 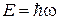й імпульсом 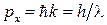. У загальному випадку, вектор , тоді під експонентою коштує скалярний добуток , і хвильова функція описує електрон, який рухається в напрямку вектора .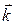

Рівняння Шредінгера

Тепер, коли ми ввели поняття хвильової функції, необхідно визначити рівняння, якому воно підкоряється. У попередньому розділі наведено вираз для хвильової функції вільної частки 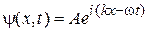, використовуючи яке можна трактувати досвіди із спостереження інтерференції на двох щілинах. Давайте подивимося, як одержати із хвильової функції імпульс 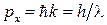і енергію 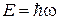. Нагадаємо, що для вільної частки кінетична енергія 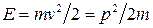, де - швидкість. Для цього помітимо, що

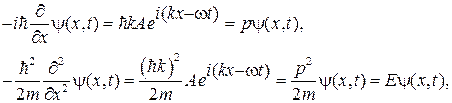(2)

Таким чином,

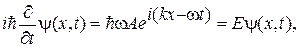(2а)

Порівнюючи (2) і (2а), одержимо рівняння Шредінгера для вільної частки

(3)

Зовнішня потенційна енергія приводить до зміни повної енергії частинки . У результаті маємо рівняння Шредінгера для частинки в потенційному полі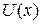

(4)

Помітимо, що (4) - стаціонарне рівняння Шредінгера, оскільки потенційна енергія не залежить від часу, при цьому залежність хвильової функції від часу має вигляд: 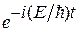. Узагальнення на простір більш високої розмірності (наприклад, 3D - тривимірне): .

Якщо задано потенціал, рішення рівняння (4) можна знайти аналітично або чисельно. У результаті, знаходимо власні функції 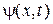й набір власних значень 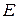. Рівняння Шредінгера – диференціальне рівняння другого порядку. Щоб одержати рішення, необхідно задати систему граничних умов для самої хвильової функції і її першої похідної.

Стан однієї частинки

Для вільної частинки граничні умови, що накладаються на хвильову функцію, задаються залежно від фізичної картини досліджуваного об'єкта. Поки що ми розглянемо, у яких станах може перебувати одна частинка, а в наступних розділах перейдемо до питання про заселення цих станів. Оскільки в рамках елементарної картини передбачається, що електрони не взаємодіють один з одним, то питання про знаходження хвильової функції й енергії електронів має першорядну важливість.

У наноелектрониці звичайно зіштовхуються із трьома типами приладів, структурна геометрія яких зводиться до показаного на рис. 2.

а б в

Рис. 2. (а) - квантова яма; (б) - квантовий провідник; (в) - квантова крапка.

Квантова яма. У квантових ямах (а), рух електронів обмежено тільки в одному вимірі (у цьому випадку по осі z)|. Квантові ями звичайно одержують шляхом напилювання на шар речовини (звичайно, напівпровідник) інших матеріалів з більше меншою шириною забороненої зони (див. рис. 3.).

На рис. 3. показано рельєф потенційної енергії, що відповідає дну зони провідності, нижче якої перебуває заборонена зона. Привернемо увагу, що на малюнку зображено дві потенційні ями, на основі сполук GaAs і Al_xGa_1-xAs.

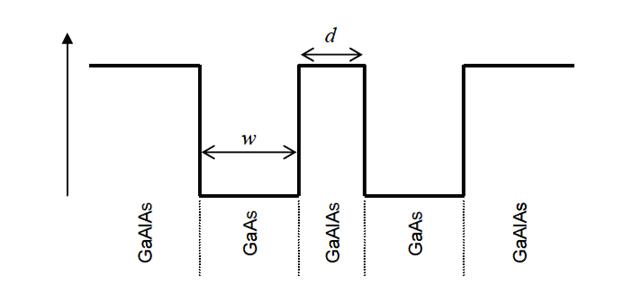
Рис. 3. Структура квантових ям.

Така шарувата структура (гетероструктура) звичайно вирощується за допомогою молекулярно-променевої епітаксії (МПЕ) або Мос-Гібридної епітаксії (газофазна епітаксія з металоорганічних сполук). Відомо, що ширина забороненої зони GaAs при кімнатній температурі близько 1.5 еВ (точніше, 1.424 еВ), а для потрійного розчину Al_xGa_1-xAs зростає до 2.2 еВ з ростом концентрації алюмінію x. Таким чином, якщо електрон попадає в область матеріалу з меншою шириною забороненої зони (GaAs), він там і утримується, вільно переміщаючись у поперечній до осі Z площині. Попутно нагадаємо, що по ряду деяких параметрів арсенід галію набагато перевершує інші напівпровідники сучасної електроніки, так, наприклад, він має більш високу рухливість електронів, що дозволяє приладам працювати на частотах до 250 ГГц. На жаль, по іншим фізичним характеристикам GaAs — більше тендітний і менш теплопровідний матеріал, чим кремній. Підложки з арсеніду галію набагато складніші для виготовлення й приблизно вп'ятеро дорожче, ніж кремнієві, що обмежує застосування цього матеріалу. До того ж токсичні властивості арсеніду галію детально не досліджені, але продукти його гідролізу токсичні (і канцерогенні).

Отже, розрахуємо поводження електрона у квантовій ямі, зображеної на рис. 2. У поперечному напрямку, площина XY, рух вільний, а в напрямку Z - обмежено потенційними бар'єрами. Природно припустити, що хвильова функція на границі яма-бар'єр повинна дорівнювати нулю. Іншими словами, імовірність знаходження частинки усередині бар'єра дорівнює нулю. Найбільш підходящий кандидат для такого рішення - 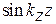. Дійсно, синус у нулі є нуль. Отже, використовуючи хвильову функцію для вільної частинки з попереднього розділу, одержимо хвильову функцію частки у квантовій ямі

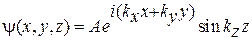, (5)

де 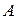визначається з умови нормування, див. (1). Із граничної умови 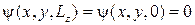витікає , де 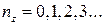Відзначимо, що всі позитивні, таким чином, позитивне й відповідне хвильове число. Це наслідок того, що негативні значення відповідають тому ж самому рішенню. Інша картина для хвиль, що біжать: 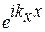рішення відрізняється від 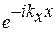, та й фізична інтерпретація для них різна - одна хвиля поширюється в позитивному напрямку, у теж час як інша - у негативному. Оскільки поперечні розміри в шарі значно перевищують поздовжні (по Z), варто очікувати слабку залежність рішення рівняння Шредінгера від структури граничних умов у цих напрямках. Звичайно використовуються періодичні граничні умови: рішення на границі збігаються. А саме, 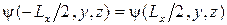, і аналогічно по осі Y. У цьому випадку , або =1, , де .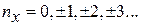

Ми вже обчислювали енергію вільної частинки, див. рівняння (2). Вираз для енергії частки у квантовій ямі перебуває шляхом узагальнення й використання, отриманих із граничних умов, значень хвильових чисел. У результаті маємо

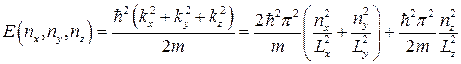. (6)

Помітимо, що оскільки поперечні розміри значно перевищують поздовжній, другий доданок у сумі при однакових числах 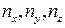буде значно більше першого.

Квантове проведення (б). Це вже модель провідника. Нам надалі знадобиться обчислити провідність такого роду структур, тому необхідно вивчити квантову механіку окремого електрона. Хвильова функція й спектр власних значень визначаються граничними умовами. У цьому випадку рух електрона обмежено із двох сторін і по одному напрямку провідник має значно більшу довжину. У зв'язку цим, хвильова функція звертається в нуль на границях і в поздовжньому напрямку - періодичні граничні умови. Енергія електронів

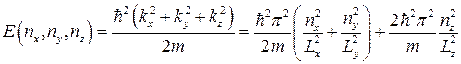, (7)

де 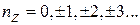, а інші квантові числа позитивні. Перший доданок в (7) - поперечні моди. Тут можна привести аналогію з збудженням електромагнітних коливань у витягнутому резонаторі або хвилеводі. Як видно, через те що поперечні розміри малі в порівнянні з поздовжніми, енергетичні масштаби поперечних мод значно перевищують поздовжні. Стани одного електрона будуть визначатися значенням хвильових чисел 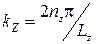; відстань між сусідніми значеннями буде 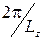. Якщо взяти «довжину» , легко підрахувати число станів. Для цього повну довжину необхідно розділити на відстань між сусідніми значеннями. У результаті маємо

«кількість станів» = (8)

де ми використовували зв'язок між імпульсом і хвильовим числом 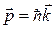. Для поперечних мод не буде двійки в знаменнику, відстань між поперечними рівнями енергії буде значно більше, ніж між поздовжніми, але не можна забувати, що їхні хвильові числа позитивні, у той час як поздовжні моди можуть поширюватися як у позитивному, так і в негативному напрямку просторової осі.

Рис.4. Енергія електронів усередині квантового провідника.

На рис. 4. представлено картину розподілу енергетичних станів відповідно до (7). У кожному стані може перебувати електрон. Поздовжні стани розташовані більш густо, ніж поперечні. Надалі, для розгляду питань провідності необхідно відповісти, у даному контексті, на два питання: 1. Як будуть заселятися стани електронами; 2. Скільки поперечних мод буде задіяно.

На ці питання одержимо питання, коли будемо розглядати розподіл багатьох електронів.

Що стосується квантової крапки (в),електрони утримуються в трьох просторових напрямках. Природно припустити, що хвильова функція буде звертатися в нуль на границях і енергію можна записати у вигляді:

. (9)

Для приклада розрахуємо два кубічних ( ) провідники, один із яких має розмір 5нм, іншої – 1мм. Структура енергетичних рівнів визначається з рівняння (9). Знайдемо інтервал між першим і другим рівнем. Для цього треба змінити одне квантове число 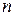на одиницю, залишаючи інші незмінними. Таким чином,

,

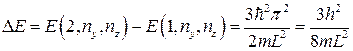де ми використовували 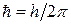. У наноелектроніці як одиниця виміру енергії використовується електрон-вольт (еВ) – енергія, що здобуває електрон при проходженні різниці потенціалів 1В. Помноживши електрон-вольти на заряд електрона 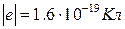, одержимо енергію в Джоулях. Зупинимося докладніше на обчисленні комбінації 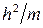. Нагадаємо, що МеВ (енергія спокою електрона), де - швидкість світла. Отже,

.

Для 5 нм провідника маємо =0.015 еВ, у другому випадку 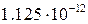еВ. Таким чином, переходячи до макроскопічних масштабів, одержуємо практично безперервний спектр енергій, у той час як на наномасштабах на перший план виступає дискретність енергетичних рівнів, які скоріше нагадує рівні ізольованого атома.

Опір балістичного провідника

Для того щоб вирішити чи використовувати модель балістичної провідності, необхідно знайти довжину хвилі Фермі й зрівняти її з розмірами системи (звичайно поперечними). Якщо довжина хвилі порівнянна із розміром і немає істотних нерегулярностей, то ми перебуваємо в балістичному режимі. Якщо взяти, приміром, GaAs, характерна поверхнева щільність носіїв заряду в якому дорівнює , то з формул знаходимо .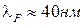

Розглянемо шматок провідника, що розташовано між двома великими контактними площадками, як показано на рис. 9 (в). Якщо б розміри провідника були великими, то ми знаємо, що його кондактанс (провідність) буде визначатися як 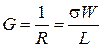, де 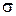- питома поверхнева провідність. Надалі, для цих величин ми будемо використовувати терміни: кондактанс і коефіцієнт провідності. Помітимо, що зараз працюємо з планарними (поверхневими) структурами. Із формули для кондактанса витікає, що якщо зменшується, то кондактанс збільшується необмежено. Експериментально, однак, було показано, що обмірювана провідність наближається до граничного значення й кінцевого опору , коли довжина провідника стає набагато менше, ніж довжина вільного пробігу.

Звідки виникає цей кінцевий опір? Адже, якщо електрони ні на чому не розсіюються, опір повинен бути дорівнювати нулю. Дійсно, рух електронів у цьому випадку, скоріше нагадує траєкторії більярдних куль. Та й квантова механіка не може дозволити такий парадокс. Ми просто заміняємо електрон на електронну хвилю й, якщо хвилі не на чому розсіюватися, вона буде поширюватися без загасання. Для того щоб знайти вихід з даного протиріччя, природно припустити, що кінцевий опір виникає в результаті взаємодії між провідником і контактними площадками, які складаються з різних матеріалів. Із цієї причини ми будемо думати про цей кінцевий опір балістичного провідника, як про контактний опір. Коли ми говоримо про різні матеріали провідника й контактів, то маємо на увазі, насамперед, геометричні особливості й характерні розміри. Основне завдання контактів – поставляти електрони в провідник із заданим хімічним потенціалом (енергією). У контактах електрони розподілено відповідно до розподілу Фермі-Дірака із певним значенням енергії Фермі. Якщо вважати, що контакти – двовимірні структури, які отримано в результаті напилювання, то електрони розподілено по поздовжнім і поперечним модам однаково, іншими словами, ми бачимо ізотропну картину. У самому ж провіднику енергія електронів має вигляд як на малюнку 4. Є набір поздовжніх станів, структура яких визначається розмірами системи; основна їхня особливість у тім, що вони розміщені дуже густо, відстань між ними в просторі хвильових чисел дорівнює . З іншого боку, існують і поперечні моди, які більш сильно рознесені по енергії. Зокрема, ( 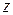- поздовжня координата, - поперечна). Нагадаємо, що в поперечному напрямку ми приймаємо для хвильової функції умова обігу її в нуль на границі, тому 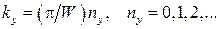Таким чином, ми знайшли розходження між контактами й провідником: якщо в провіднику електрони можуть перебувати в станах з більшою кількістю поперечних мод, то в провіднику їх буде кінцеве значення. Іншими словами, існує якась несумірність у розподілі по поперечних модах. У контактах вони розташовані дуже густо, , де - характерний розмір контакту, і їх можна вважати нескінченно багату кількість, а в провіднику рідко, внаслідок того що 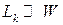. Отже, можна вважати, що контактний опір - це результат перерозподілу електронів по модах при переході з контакту в провідник. Звичайно, ми позбудемося від цього контактного опору, просто зробивши контакти ідентичними провіднику. Але в цьому випадку ми вийшли б з області наноелектроніки й проблема втратила б зміст. У кожному разі, по розміру контакти набагато більші, ніж нанопровідники. І якщо зробити контакти з нанопровідників, у якому розподіл по модах буде таким же, той контактний опір буде відсутній, але не можна забувати, що ми повинні використовувати ще контакти для наших нових наноконтактів, до яких можна було б приєднати зовнішнє джерело. Від контактного опору ніяк не піти. Помітимо ще, що якщо подати напругу на систему контакти-нанопровідник, спадання напруги буде зосереджено на переходах контакт-провідник. Для того щоб обчислити струм, треба розглянути, що відбувається на контакті між резервуарами електронів (контакти 1 і 2 на малюнку 9(в)) і, властиво, нанопровідником.

Безвідбивні контакти.Для розрахунку контактного опору ми розглянемо балістичний провідник і розрахуємо струм через нього для даної різниці хімічних потенціалів (енергій) між двома контактами , при цьому не можна забувати, що заряд електрона негативний, тому якщо напруга джерела 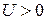, те . Для розрахунку струму необхідно зрозуміти, що відбувається, коли електрони входять із контакту в провідник. Це складне завдання, що, однак була вирішена в 1989 році шляхом чисельного моделювання проходження електронів з контакту в провідник. Було показано, що коли електрони виходять із провідника в контакт, то вони розсіваються в перехідній області із дуже малою ймовірністю. Іншими словами, можна вважати, що процес входу в контакт із провідника носить практично безвідбивний характер. З іншого боку, коли електрони виходять із контакту в провідник, вони сильно розсіваються. Це можна зрозуміти з наступних міркувань. У контакті багато вільних станів, це, фактично, макроскопічний об'єкт, основне завдання якого поставляти електрони в провідник, а в провіднику - всі стани (рахункове число) вільні доти, поки не потече струм; у цьому випадку вони будуть зайняті, причому в одному стані буде не більше одного електрона.

Рис. 10. Випадки встановлення рівноваги між контактом і провідником.

Таким чином, ніщо не буде перешкоджати електрону покинути провідник і зайняти вільні стани в контакті. Інша справа, зворотний процес, коли електрони з контакту намагаються вийти в провідник. Наочно можна уявити собі дві залюднені кімнати, з'єднані вузьким коридором. Людина, що знаходиться біля коридору, може зайти в нього тільки в тому випадку якщо коридор вільний, а вийти з коридору може безперешкодно в кожному разі. Таким чином, вихід - без опору, а весь опір на вході.

Тепер припустимо, що в провіднику є зайняті електронні стани й приєднаємо до нього один контакт. Подивимося як буде встановлюватися рівновага між контактом і провідником. Наочна картина зображена на рисунку 10.

Ні малюнку 10 показано енергетичні характеристики електронів усередині провідника, 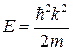для кожної поперечної моди. Для простоти думаємо, що їх тільки дв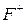і . і 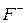- рівні енергії Фермі для електронів, які рухаються в позитивному й негативному напрямку осі , відповідно. - хімічний потенціал контакту. Коли , як на рис 10(а), електрони йдуть із провідника в контакт. При цьому хімічний потенціал контакту не змінюється, а перехід електронів відбувається із кінцевим опором, і скоріше нагадує процес дифузії. Причому йдуть електрони, які рухаються ліворуч, до контакту. У результаті стани 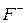спорожніють аж до енергії . Таким чином, усередині провідника встановиться асиметричний розподіл електронів, коли стани 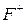не змінюються, а 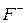практично спорожніють. Подальшої еволюції не буде, оскільки стан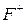и й 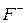не взаємодіють один з одним. Якщо ж , як на рис 10(в), то електрони будуть входити із контакту в провідник, заповнюючи стани 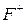. Рівноважна ситуація показана на рис.10(с) і не вимагає обговорення.

Приєднаємо два контакти з хімічними потенціалами . Рівноважний випадок, коли , показано на рис. 11(а). У цьому випадку електрони з лівого контакту заповнюють стани, які поширюються в позитивному напрямку осі , до енергії усередині провідника 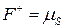. Аналогічно з електронами із правого контакту, але тільки до .

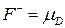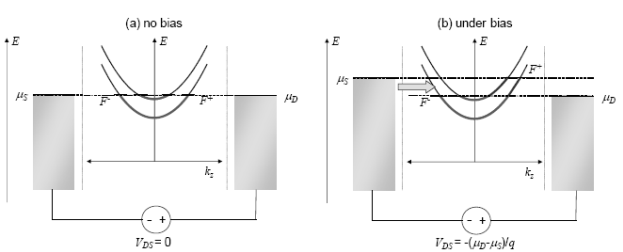
Рис. 11. Два контакти.

Коли подається напруга на контакти, їхні хімічні потенціали змінюються на величину . Оскільки , електронів з локальною енергією Ферми 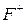буде більше чим електронів с. 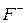У результаті в системі потече струм, тому що потік електронів у позитивному напрямку буде більше, ніж у негативному. На малюнку 12 зафарбованим прямокутником зображено шар електронів, які, власне кажучи, дають внесок у струм.

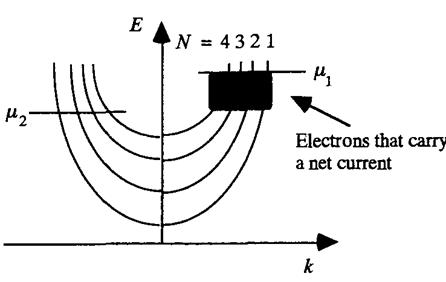
Рис.12. Дисперсійне співвідношення для електронів усередині провідника при заповненні чотирьох поперечних мод. Електрони з лівого контакту заповнюють стани до 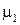, а із правого до . У зафарбованому прямокутнику електрони, що дають внесок у струм.

Тепер, коли ми познайомилися з питанням про взаємодію провідника з контактами, перейдемо до одержання формули для струму. Нагадаємо, що в даному випадку електрони рухаються в одному напрямку, а облік поперечного руху приводить тільки до необхідності підрахунку числа поперечних мод. Природно, може трапитися, що кожна поперечна мода вносить свій, відмінний від інших, внесок у струм; тоді розрахунок струму значно ускладниться. На щастя, це не так: всі поперечні моди вносять однаковий вклад у струм. Це тим більше дивно, що, дивлячись на мал.11, бачимо, що інтервали станів по хвильових числах 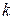(зафарбований прямокутник) будуть різні для кожної поперечної моди. Але справа в тому, що для струму в одному вимірі є важливим не інтервал по 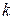, а різниця енергій (вертикальна вісь на рис.11), яка для всіх мод однакова.

Визначимо струм для одномірної системи. Нехай електрони входять із лівого контакту в провідник зі швидкістю 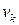(швидкість електрона із хвильовим числом 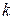) і залишає його, ідучи в правий контакт. Який струм переносить цей один електрон? З визначення струму, заряд розділений на час, витікає, для одного електрона. Проблема у тім, який береться час. Отут вступає в дію принцип Паулі, а саме, в одному стані – тільки один електрон (без обліку спина). Таким чином, поки електрон у певному стані перебуває в системі, інший електрон у такому ж стані не може влетіти в провідник. Електрон пролітає провідник довжиною за час 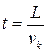. Звідси треба, що струм одного електрона дорівнює 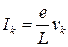. Загальний струм знаходиться підсумовуванням по всіх станах 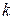. Причому, як ми з'ясували раніше, частина електронних станів рухається в позитивному напрямку 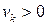, інші в негативному 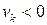, їхній внесок у струм компенсує один одного, залишаться тільки електрони які перебувають в інтервалі енергій . У формулі для струму зараз все відомо, крім швидкості. Тут діє просте правило: якщо електрон має енергію 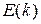, його швидкість дорівнює 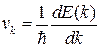. Дійсно, для квадратичного закону дисперсії 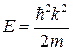маємо 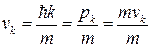. Слід зазначити, що формула для знаходження швидкості працює для будь-якого закону дисперсії, якщо тільки не маємо справу з релятивістськими частинками. Отже, вираз для струму має вигляд

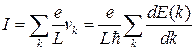, (22)

Де підсумовування поширюється по всіх поперечних модах і попадає в енергетичний інтервал . У випадку, коли , легко перейти від підсумовування до інтегрування 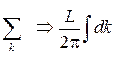. Застосовуючи цю формулу, одержуємо для однієї поперечної моди

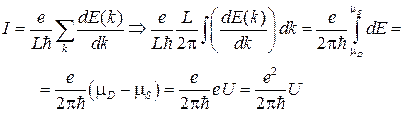(23)

Що зміниться, якщо в нас є