Квантова модель вільних електронів

У моделі Друде, яку ми тільки що обговорювали, неявно передбачається наступне: електрони не взаємодіють один з одним і кристалічною решіткою; електрони можуть мати будь-яку швидкість і, отже, енергію; всі електрони в провіднику дають внесок у провідність; статистичний розподіл електронного газу - розподіл Максвелла-Больцмана.

Перше припущення може бути виправдано для більшості металів, де потенціали окремих атомів і взаємодія електронів один з одним ефективно екранується у зв'язку з високою щільністю електронів. Однак для напівпровідників ситуація інша: внаслідок взаємодії електронів з періодичною кристалічною решіткою утворюється заборонена зона. Проте, можна вважати, що в регулярній решітці електрони усередині провідника не взаємодіють один з одним, вони займають певні енергетичні стани, аналогічні станам вільних електронів, а кристалічна решітка приводить до зміни деяких параметрів носіїв заряду. Зокрема, маса електронів міняється на ефективну масу. Таким чином, у більшості випадків добре працює модель вільного електронного газу.

Друге припущення не є життєздатним, тому що квантова механіка говорить нам, що енергія електронів у провіднику буде мати певні, дискретні значення. Нарешті, електрони є ферміонами, і, як відомо, підкоряються статистиці не Максвелла-Больцмана, а Фермі-Дірака. Ці факти в остаточному підсумку приводять до провалу моделі Друде, яка просто не може пояснити велику кількість явищ, наприклад, конкретні теплові властивості матеріалів, електричний опір у наноструктурах, та й багатьох інших.

Основний закон, який управляє електронами, - принцип заборони Паулі. Він говорить: в одному стані може перебувати тільки один електрон. Це незвичайна ситуації з погляду класичної фізики. Так, наприклад, принцип заборони Паулі приводить до того, що в окремому провіднику не можуть перебувати два електрони з однаковими імпульсами (і спінами). В класиці така заборона суперечить здоровому глузду. Частинки, на які поширюється ця заборона, називаються ферміонами (на честь Энріко Фермі, який побудував статистику частинок, що підкоряються принципу заборони). Не можна забувати, що стан частинки може характеризуватися не тільки динамічними характеристиками (імпульс і ін.), але й внутрішніми змінними, такими як, наприклад, спін. Зокрема, нам треба знати, що у електрона є два стани спіна. Іншими словами, число станів збільшується вдвічі. Хоча, якщо помістити електронний газ в сильне зовнішнє магнітної поле, всі спіни будуть орієнтуватися по напрямку поля, таким чином, буде зайнятий тільки один спіновий стан.

Оскільки існує кінцеве число електронів у провіднику, енергетичні стани послідовно заповнюються по мірі зростання енергії до певної величини (енергія Ферми, ), як показано на рис. 6.

Нагадаємо, що стани в ідеалізованій одномірній моделі (рис.6. ліворуч) будуть розташовуватися на параболі 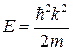з інтервалом по хвильовим числам , де - розмір системи. Якщо ж , то енергетичні стани будуть практично безупинно розподілені. У тривимірному випадку корисно вважати, що електронні стани представлено крапками усередині поверхні Фермі (див. рис. 6. праворуч). Однак в наноелектроніці найчастіше мають справу з обмеженим набором носіїв заряду, тому на перший план виступає завдання про рахункове число станів, ідучи від безперервної моделі. Звичайно наноструктура складається з контактів, по яких підводять у систему електрони, і властиво приладу.

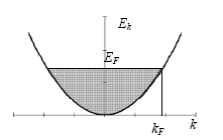
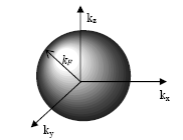
Рис.6. Ліворуч - дисперсійне співвідношення в моделі вільних електронів; праворуч - сфера Фермі в ізотропній моделі.

Таким чином, доцільно підходити до проблемі провідності наноструктур у такий спосіб. Контакти вважаються ізотропними провідниками, що перебувають у рівноважному стані. Іншими словами, явища, що відбуваються усередині наноструктури ніяк не впливають на стан контактів. Потім необхідно розглянути стани вільних електронів усередині наноструктури, виходячи з її геометрії. Далі, електрони попадають із контактів і заповнюють ці внутрішні стани, по яких можна підсумувати і знайти, приміром, струм, який, у свою чергу, буде визначатися станами контактів.

Визначимо енергію й імпульс Ферми для тривимірного ізотропного провідника. Нехай у системі є 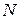електронів. Тоді ці електрони заповнюють всі стани аж до енергії Ферми 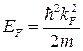. «Об'єм» в 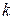- просторі, який займає один стан (періодичні граничні умови) дорівнює 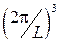. Таким чином, кількість станів можна визначити, розділивши повний об'єм Фермі сфери 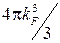на об'єм одного стану. З огляду на те, що через наявність спіну в кожному стані може перебувати два електрони, маємо

(13)

де 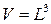- просторовий об'єм системи. У результаті

(14)

де - щільність електронів. Наприклад, якщо взяти золото, що має енергію Ферми 5,51 еВ, одержимо, що концентрація (щільність) електронів дорівнює , що відповідає приблизно одному електрону на атом. Така ситуація - звичайна справа для металів.

Надзвичайно важливою величиною для фізиці твердого тіла, як і в наноелектроніці, є число станів на одиницю енергії в інтервалі й в одиничному об'ємі, яку називають щільністю станів 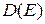матеріалу. Отже, щільність станів визначається як і є диференціальна характеристика. Для того щоб знайти щільність станів, нагадаємо формулу для елемента об'єму в к-просторі 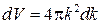. Таким чином, число станів в елементі об’єму 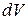дорівнює

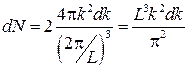(15)

Або для щільності маємо

(16)

У двовимірному випадку, коли є обмеження для руху електронів в одному напрямку, як у квантовій ямі, рівень Фермі визначається в такий спосіб:

(17)

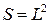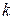де - поверхнева щільність електронів, - площа. Далі знайдемо щільність станів, що визначається як . Елемент площі в -просторі дорівнює 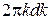( за аналогією зі звичайним 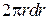). Площа , яку займає один стан в 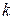-просторі дорівнює . Щоб знайти кількість станів, треба елемент площі розділити на площу одного стану й не забути про двійку через спина. У результаті

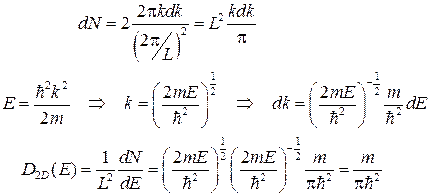(18)

На відміну від тривимірного випадку, коли щільність станів зростає з ростом енергії як 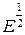, для планарних структур (квантових ям і т.д.) щільність взагалі не залежить від енергії.

В одному вимірі, тобто для квантового дріту, кількість станів . Додаткова двійка в чисельнику виникла через те, що в нас є два сорти часток – одні рухаються в позитивному напрямку (права галузь параболи 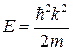), інші, у негативному.

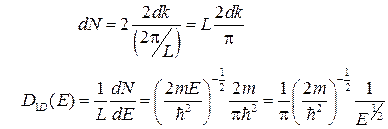(19)

Припустимо, що в нас є набір енергетичних рівнів 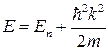. Ми вже зіштовхувалися з подібною ситуацією, коли розглядали поперечні моди у квантовому дріту. Тоді, як легко переконатися, повторивши математичні викладки, у щільності станів (19) , тобто на кожному рівні щільність станів в одномірному випадку звертається в нескінченність, є сингулярність, показана на рисунку 7.

Дотепер ми не враховували вплив температури, і наш аналіз дійсний тільки при нульовій температурі. Коли температура збільшується, кінетична енергія електронів у провіднику також буде збільшуватися, що приводить до «размиття» поверхні Ферми. Це відбувається внаслідок того, що електрони під дією температури переходять зі станів під поверхнею Фермі у вільні стани над нею. Якщо раніше ми говорили про чітку границю, що нагадує сходинку, то тепер ця границя згладжується.

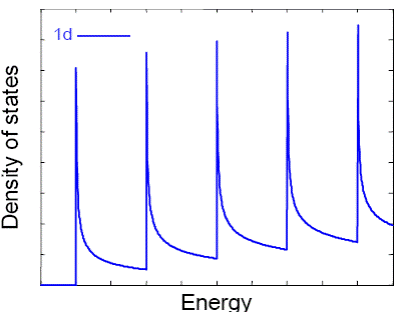
Рис.7. Залежність щільності станів від енергії у квантовому дріту.

З іншого боку, при нульовій температурі ми заповнювали стани за правилом: є вільної незайнятий стан при енергії 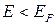, з імовірністю рівній одиниці воно заповнювалося. Іншими словами, уважалося, що всі стани рівноймовірні. Природно, що температура руйнує таку концепцію, приводячи до відмінної від нуля ймовірності знаходження частинки в стані із заданою енергією. Ця ймовірність і є функція розподілу Фермі-Дірака

, (20)

де - постійна Больцмана; - хімічний потенціал провідника, що визначається як енергія найвищого заповненого стану при нульовій температурі, так, якщо провідник перебуває під потенціалом , то 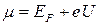. Якщо помножити щільність станів на розподіл Ферми , одержимо щільність заповнених станів.