Теоретические предпосылки метода механической прогонки

Главной целью данной диссертационнойработы является создание метода механической прогонки. Проанализируем теоретические разработки, в основе которых заложена идея метода прогонки-перенос граничных условий. Метод прогонки был сформулирован в среде отечественных математиков при численном решении дифференциальных уравнений второго порядка с заменой производныхконечными разностями [9,10,11,84] . Граничные условия одного края одномерной области последовательно переносятся по приращениям аргумента к другому краю и связываются разрешающими уравнениями граничных условий на нём. Решение методом прогонки задачи тёплопроводности однородного стержня [83] можно рассматривать как применение прогонки в двумерной области: - длины стержня и времени. Однако расчёт напряжённо-деформированного состояния двумерных оболочечных конструкции в сравнении с задачами теплопроводности по причине больших значений модуля Юнга связан с использованием разностей близких друг к другу малых величии. При быстроменяющихся разрешающих функциях в этих задачах возможна потеря точности, вызванная аппроксимацией производных конечными разностями значений функций.

Дальнейшее развитие методов прогонки потребует увеличения числа решенных уравнений в алгоритме переноса граничных условий по приращениям аргумента. В известных работах с использованием метода прогонки это число решенных уравнений находится в пределах 2-3, В задачах расчёта НДС оболочекна приращениях аргументов координат x и у необходимо учитывать значительно большее число степеней свободы - шесть.

Препятствием в развитии метода прогонки в задачах упругости и пластичности твердых тел является использование условий совместности деформации в форме Сен-Венана. Поэтому предполагается это условие в методе механической прогонки применять в форме перекрестных связей.

Ещё одно обстоятельство, требующее анализа, состоит в том, что алгоритм переноса граничных условий в известных вариантах мегода прогонки основан на формулах, непосредственно полученных из дифференциальных уравнений. Использование дифференциальных уранений имеет смысл в тех случаях, где найдены аналитические решения. Однако в случаях, где аналитические решения дифференциальных уравнений не найдены решение их методом конечных разностей производится в отрыве от специфики механических условий. При этом теряется ценная информация. Поэтому имеет смысл рассмотреть перенос граничных условий на основе формул, полученных из решения системы физических уравнений, записанных для малых приращений параметров и других уравнений механики.

Заканчивая анализ методов прогонки, отметим, что в разрабатываемый метод механической прогонки из известных войдёт только постановка задачи, состоящая в переносе граничных условий. Метод начальных параметров также основан на переносе граничных условий по приращениям аргументов дифференциальных уравнений [85,86,67]Он позволяет решать задачи расчёта устойчивости и собственных частот сложных стержневых сооружений [88,89]. При этом определяется не значения искомой функции дифференциального уравнения, а косвенно входящие параметры из условия наличия ненулевых решений разрешающей системы уравнений. Данный метод можно развивать по пути применения к двумерным задачам оболочек, где процедуры переноса граничных условий потребуют решения большего числа уравнений на каждом ваге приращений аргумента.

Метод диакоптики был сформулирован американским учёным Г. Кроном [90,91,92] для расчета электрических и механических сетей. Он заключается в разделении на части модели исследуемой системы, решений этих частей отдельно с последующим объединением решений отдельных частей в решение всей системы. Механические системы были им рассмотрены на примере балочных конструкций. В этой передовой разработке усматривается выход при решении современных задач техники, рассматривающих бесконечную систему элементов. В приведённых решениях задач механики проводилась аналогия между механическими параметрами и электрическими. По этой причине не учитывалась в полном объёме специфическая информация механических условий, в частности перекрёстных связей внутри элементов. Однако Г. Крон по-видимому прав в части критики, утверждая, что инженерымеханики никогда не использовали даже наиболее элементарные понятия комбинаторной топологии .

До настоящего времени работы Г. Крона не поняты до конца из-за наличия в них незаконченности и нестрогости рассмотрения. Метод диакоптики следует считать находящимся на стадии постановки задач. Сущность его предстоит раскрыть. Однако сам факт того, что за рубежом ведутся работы по созданию родственного метода диакоптики подтверждает актуальность цели настоящей работы - создание метода механической прогонки.

Метод механической прогонки, сущность которого будет заключаться в переносе граничных условий, должен представить новое направление механики - трансляцию граничных условий по механической системе, представляющей собой совокупность большого количества связанных элементов [94].

4.2. Алгоритм переноса граничных условий на примере расчёта пластины

Рассмотрим метод на примере двумерной задачи расчёта напряжённо-деформированного состояния жёстко заделанной квадратной пластины. Пластина шириной Ь и толщиной h нагружена давлением q. Поместим её в систему декартовых координат . (рисунок 4.1). Разделим мысленно пластину параллельными линиями на n интервалов по осям X и Y соответственно (штриховые линии на рисунок 4.1). Индекс i соответствует сечениям по оси X, индекс j – сечениям по оси y. Из числа элементов n² выделим один с i-м нижним и j-м левым сечением (рисунок 4.2). Ширина элемента: .

В каждом сечении элемента пластины будет действовать переменная эпюра напряжений. При уменьшении размеров элементов в сечении согласно принципам механики для твердого тела напряжённое состояние можно представить силами, сосредоточенными в центре и моментами. Для таких деформаций пластины с симметричным нагруженном касательными и нормальными силами по осям х и y можно пренебречь [96]. Таким образом в каждом сечении будем учитывать: изгибавший момент М вокруг срединной линии, параллельной плоскости пластины, крутящий момент К и перерезывающую силу , параллельную вертикальной оси Z.

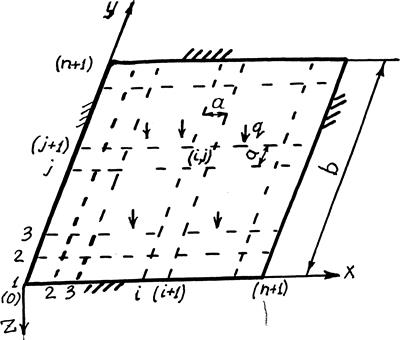Рисунок 4.1 - Схема расчеления пластины на элементы

Угол поворота от изгибающего момента будем обозначать , угол поворота от крутящего момента - 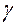, перемещение в направлении перерезывающей силы –W. На (рисунке 4.2) показано положительное направление этих перемещений. Параметры М, К, , , , 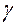w в сечениях, перпендикулярных осям х и у будем снабжать индексами х и у соответственно. Индексы i , j соответствуют номеру сечений по оси x и у.

Рисунок 4.2 - Усилия и перемещения на краях выделенного

элемента пластины

Для составления алгоритма метода механической прогонки будем пользоваться следующими уравнениями для выделенного элемента. Уравнениями статического равновесия:

; (4.1)

; (4.2)

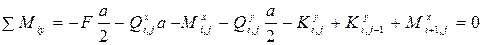. (4.3)

Здесь распределённая нагрузка q для малого элемента с достаточной степенью точностизаменена сосредоточенной силой в центре элемента: (4.4)

Как показали экспериментально-теоретические исследования [28, 83] моделирование распределённой нагрузки эквивалентной системой дискретных сил достаточно точно обеспечивается для элементов оболочек при числе сил 8.

Физические уравнения, полученные на основе закона Гука и гипотезы прямых нормалей для элемента пластины [24]

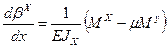; (4.5)

; (4.6)

; (4.7)

. (4.8)

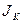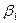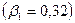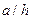Где: Е- модуль Юнга ; , - моменты инерции на изгиб ; - коэффициент Пуассона ; ; -момент инерции на кручение ; - малоизменяемый коэффициент [97] при >10.

В дальнейшем предполагается для каждого элемента задавать разные значения нагрузок F, модуля E, геометрических размеров. Это позволит решать задачи несущей способности конструкций с учётом теплового и динамического нагружения, анизотропии свойств [98,99,100,101].

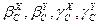Уравнения совместности деформаций используем в форме метода перекрёстных связей, развитие которого получило в работе [24]. В центре элемента перемещения ( ) и углы поворота ( ) равны, если каждый элемент рассматривать как окончание балки, идущей по оси Х с одной стороны и окончание балки, идущей по оси У с другой стороны (рисунок 4.З).

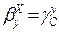; (4.9)

; (4.10)

(4.11)

Рисунок 4.3 – Схема расположения элемента на перекрестных связях

Углы поворота и перемещения в центре определим интегрированием упругой срединной линии элемента. Интегрирование проводим с использованием производных в соотношениях (4.5) - (4.6), отдельно двигаясь по оси X от левого сечения направо к центру и по оси У от нижнего сечения вверх к центру элемента (рисунок 4.2). Получим. с учётом (4.9 – 4.11)

; (4.12)

(4.13) (4.14)

Условияна границе элемента зависят от параметров предыдущих элементов.

Прогонка по механическим параметрам начинается с граничных условий, где для жёстко заделанной пластины [94]

; (4.15)

; (4.16)

Например, начиная с левого нижнего элемента пластины, выразим : из системы (4.12) - (4.13) через (рисунок 4.4). В последующем параметры всех элементов будем выражать через неизвестные силовые факторы на левой границе пластины и силовые факторы на верхней границе пластины . Прогонку проводим снизу вверх по каждой вертикальной полосе и, выразив параметры последнего верхнего элемента, переходим к следующей вертикальной полосе элементов слева направо.

Рисунок 4.4 – Схема расчленения пластины на элементы с обозначением индексов силовых факторов на краях для составления алгоритма прогонки

При рассмотрении последующих элементов начальные условия на их границе определяют интегрированием упругой линии элемента по оси y

(4.17)

; (4.18)

(4.19)

и по оси X

(4.20)

(4.21)

(4.22)

Центральной процедурой прогонки является, определение для любого элемента с номером ( i , j ) силовых факторов на верхней границе (рисунок 4.2) через левые боковые силовые факторы следующего верхнего элемента с номером ( i , j+1 )- 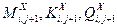. Для этого из системы уравнений (4.1)- (4.3) найдём правые боковые силовые факторы у элемента с номером ( i , j ) в зависимости от остальных силовых факторов. Подставим их в систему (4.17) - (4.19). Далее составим уравнения совместности деформаций (4.12) - (4.14) для следующего вертикального элемента с номером ( i , j+1 ), подставив туда начальные условия из системы (4.17)-(4.19) предыдущего элемента.