Метод механической прогонки в задаче расчёта нелинейного деформирования цилиндрической панели.

Исследуем возможности полученного алгоритма метода механической прогонки в задаче расчёта больших перемещений жёстко заделанной цилиндрической квадратной панели. Панель шириной b, радиуса R и толщиной h нагружена давлением q (рисунок 4.6). Поместим её в систему цилиндрических координат . Разделим мысленно панель линиями на n интервалов параллельно образующей цилиндра l₁ и перпендикулярно ей. Индекс i соответствует сечениям, параллельным образующей l₁, индекс j - сечениям перпендикулярным оси l₁. Из числа n² квадратных элементов шириной выделим один с j-м нижним и i -м левым сечением (рисунок 4.7).

В разрабатываемом алгоритме будем придерживаться тенденции к увеличению числа элементов разбиения. Это позволит с достаточной точностью элементы считать плоскими. Введём для каждого элемента местную систему координат ОXYZ.

В пределах перемещений панели, не превышающих хорду её дуги достаточно будет использовать четырёхугольные элементы, у которых в сечениях, параллельных образующей цилиндра, оставлены четыре степени свободы, а в сечениях, перпендикулярных образующей, - три степени свободы. Данная модель оболочки согласуется с теорией, изложенной в работах [102 - 120] .

В рассматриваемом случае симметричного нагружения панели в сечениях, параллельных образующей цилиндра (параллельно местным осям Оу ) будем учитывать изгибающий момент вокруг срединной линии М^у, крутящий момент К^у . перерезывающую силу Q^y , нормальную силу N^y.

Рисунок 4.6 – Схема расчленения панели на элементы

Соответственно угол поворота в направлении M^y обозначим , угол поворота от крутящего момента ,перемещение , перемещение сечения в направлении обозначим . На рисунке 4.7 Даны положительные направления деформации.

В сечениях, параллельных осям ОХ как и в случае пластины обозначим изгибающий момент , крутящий момент , перерезывающую силу и соответствующие им перемещения . Перечисленные силовые факторы и деформации будем снабжать индексами i , j соответственно номеру сечения.

Рисунок 4.7 – Силовые факторы и перемещения на краях элементов расчленения панели с обозначением индексов.

Распределительную нагрузку q для элемента заменим сосредоточенной силой в центре элемента по формуле (4.4) Исходные уравнения, на основе которых будет построен алгоритм переноса граничных условий, претерпят в отличии от пластины, следующие изменения с учетом кривизны панели:

К уравнениям статистического равновесия (4.1)-(4.3) добавится уравнение равновесия продольных сил по окружной координате (4.36)

; (4.33)

; (4.34)

; (4.35)

. (4.36)

Соответственно к физическим уравнения, полученным на основе закона Гука и гипотезы прямых нормалей для элемента (4.5) – (4.8) добавится уравнение для продольных деформаций по оси X: (4.41)

(4.37)

(4.38)

; (4.39)

(4.40)

(4.41)

Где 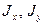- моменты инерции при изгибе ;

-момент инерции при кручении ;

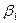-малоизменяемый коэффициент .

Аналогично расчету пластины, уравнения совместности деформаций используем в форме метода перекрестных связей. В центре элемента перемещения и углы поворота равны, если этот центр рассматривать как окончание предыдущего элемента, идущего от оси Х с одной стороны и окончание ортогонального предыдущего элемента, идущего по оси У с другой стороны (рисунок 4.7).

Отметим, что дифференциальные зависимости (4.37) – (4.41) записаны для двумерного напряженного состояния элементарных образцов, а не для балок. Поэтому балочную терминологию, принятую в работе [24] необходимо воспринимать как условную.

Углы поворота и перемещения в центре определим интегрированием упругой срединой линии элемента с использованием производных в отношении (4.37) – (4.41). При этом отдельно двигаемся по оси Х от левого сечения (рисунок 4.7) направо к центру и по оси У от нижнего сечения вверх к центру элемента. Для элемента с номером (i, j) получим равенства

; (4.42)

; (4.43)

(4.44)

Условия на границе элемента зависят от параметров предыдущих элементов. Прогонка по механическим параметрам начинается с граничных условий жестко заделанной панели, где они равны нулю.

Начиная с левого нижнего элемента пластины, выразим из системы (4.42) – (4.44) через (рисунок 4.7). В последующем, параметры всех элементов будем выражать через неизвестные силовые факторы на левой границе панели и силовые факторы на верхней границе панели и, выразив параметры последнего верхнего элемента, переходим к следующей вертикальной полосе элементов слева направо.

При рассмотрении последующих элементов начальные условия на их границе определяются интегрированием упругой линии элемента по оси У

; (4.45)

; (4.46)

(4.47)

И по оси Х:

(4.48)

; (4.49)

; (4.50)

Центральной процедурой прогонки является выражение для любого элемента с номером ( i , j) силовых факторов 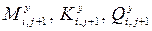на верхней границе ( рисунок 4.7) через левые боковые силовые факторы следующего верхнего элемента с номером (i , j+1) - . Для этого из системы (4.33) – (4.35) найдем правые боковые силовые факторы у элемента с номером (i ,j) в зависимости от остальных силовых факторов. Подставим их в систему ( 4.45) – (4.47). Далее составим уравнения совместности деформаций (4.42) – (4.44) для следующего вертикального элемента с номером (i , i+1), поставив в них начальные условия из системы (4.45) – (4.47) предыдущего элемента. Решение этой системы дает функции параметров .

Запись основных действий метода механический прогонки представим в матричной форме, Для этого введем вектор искомых параметров на левом и верхнем краю панели, определяемом матрицей столбцом

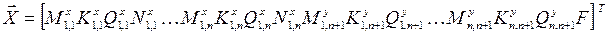(4.51)

Здесь и в дальнейшем матрицы столбцы записаны в виде строк с использованием операции транспонирования.

Последний компонент вектора (4.51) определяется известной функцией от активной силы F. Алгебраическое значение параметра с номером k из (m = 7n+1) параметров (4.51) определится скалярным произведением матрицы порядка m x m, у которой один не нулевой единичны элемент на главной диагонали с номером k, на матрицу столбец (4.51). Например

(4.52)

В последующем силовые факторы и параметры деформаций всех элементов будем выражать через вектор (4.51).

Найденные силовые параметры на верхнем краю элемента с номером (i , j) запишутся в следующем виде

. ( 4.53)

Промежуточные функции определятся из произведений матриц

(4.54)

Матрица коэффициентов, полученная автором в работе [142] имеет вид:

(4.55)

Силовые параметры нижнего края панели с учетом равенства нулю граничных условий , определяя решением системы уравнений ( 4.42) – ( 4.44).

. (4.56)

Здесь промежуточные функции выражаются через произведения матриц.

. (4.57)

Где

. (4.58)

Далее из уравнений равновесия (4.33) – (4.36) определяются силовые факторы в правом сечении элемента уже с учетом выражений ( 4.53)

·

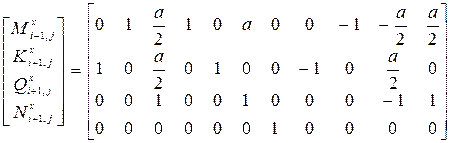· (4.59)

Постановкой силовых факторов (4.53), (4.59) в выражении (4.45) – (4.50) находятся значения деформаций в верхнем и правом сечении элемента ( рисунок 4.7) : .

Таким образом граничные условия в нижнем и левом сечения элемента перенесены в верхнее и правое сечение элемента.

При переходе к последующим элементам панели, расположенным справа от рассмотренного элемента для упрощения выражений механические параметры необходимо заменить эквивалентной системой, ориентированной вдоль осей новой местной системы координат (рисунки 4.6, 4.7). Обозначим углы между плоскостями элементов, определяемые из геометрии панели . Тогда силы и перемещения, соответствующие системе координат правого элемента, обозначения которых снабжены штрихами, выразятся в следующем виде

. (4.60)

Моменты и угловые деформации 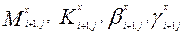останутся неизменными в новой системе .

На этом прогонка по одному элементу закончена, и перечисленные операции производятся для следующего по вертикальной полосе элемента. По окончании этой полосы переходят к следующей правой полосе, начиная с нижнего элемента (рисунок 4.6). При достижении верхнего края панели силовые параметры на нем входят в вектор искомых параметров (4.51). В этом случае действия (4.53)-( 4.55) не выполняются.

Разрешающую систему линейных алгебраических уравнений метода механический прогонки определим граничными условиями для верхнего и правого края жестко заделанной панели. Это будет 7n уравнений, которые представим матрицей столбцом:

= 0 (4.61)

В каждое уравнение может входить 7n неизвестных в порядке (4.51). Последний компонент вектора (4.51), зависящий от силы F, определит свободные члены системы уравнений.

Для расчета деформаций панели, зависящих не линейно от давления P на нее, воспользуемся методом последовательных нагружений, Давая малые приращения давления на панель q, будем определять приращения внутренних и граничных силовых факторов и деформаций. Полные значения внутренних силовых факторов и перемещений, над символами которых в дальнейшем будем ставить черту, определятся алгебраическим суммированием приращений этих параметров по числу шагов нагружений:

. (4.62)

Активная нагрузка давления P на панель определится из условия равновесия панели. Для этого по линии наибольших перемещений, в данном случае вдоль срединной образующей, мысленно рассечем панель ( рисунок 4.8). Введем ось , параллельную оси образующего цилиндра и проходящую через точку наибольших перемещений панели - ее центр. Тогда из уравнения моментов относительно оси , например для левой половины панели, в которое войдут краевые силовые факторы и силы давления, получим:

Рисунок 4.8 – Расчетная схема для составления уравнений равновесия при построении зависимости полной нагрузки Р на панель от перемещения W_с центра панели

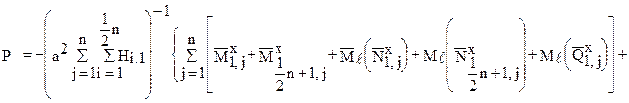
. (4.63)

Где - плечо силы , приложенной в центре элемента с номером (i , j) относительно оси ; , , , , - моменты от краевых сил для половины панели относительно оси .

Далее следует новый шаг нагружением q.

Нелинейность зависимости давления P от перемещения в центре панели в основном определяются моментами от продольных сил , . После того , как перемещения панели достигают ее хорды H ( рисунок 4.6) приращения сил , меняют свое направления на противоположенное.

Местоположение оси выбирается в области наибольших перемещений панели.

Расчеты были проведены для титановых квадратных панелей со следующими данными: b = 0,1 м; R = 1 м; h = 8 10^-4 м; E = 9,46 10¹⁰ H/м.

На рисунке 4.9а приведен расчетный график зависимости давления Р на панель от перемещения в центре ( сплошная кривая) и экспериментальный график, взятый из главы 1. Можно отметить их достаточно близкое совпадение при начальных нелинейных деформациях.

Точность расчета при определении больших перемещений панели можно повысить, доведя число учитываемых степеней свободы в сечениях элементов с четырех и трех, до максимального числа – шести.

На рисунке 4.9 представлены: графики распределения по образующей на краю панели приращений продольной силы , отнесенной к единице длины при первом шаге нагружения (q=4000Н/м²) (кривая1) и при перемещениях, превысивших хорду дуги панели ( кривая 2); график приращений перерезывающей силы , отнесенной к единице длины; график перемещений панели по срединной образующей .

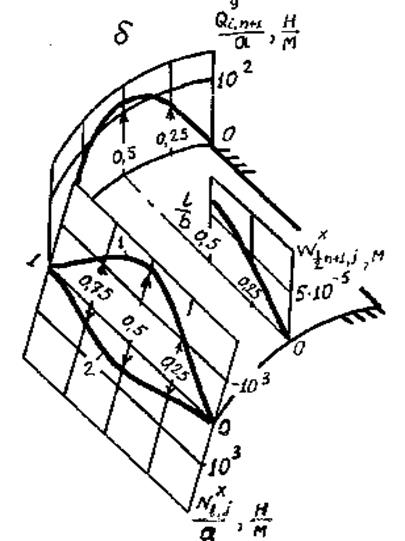
Рисунок 4.9: а – расчетный график зависимости давления Р на панель от перемещения в центре W_c ( сплошная кривая) и экспериментальный график аналогичной зависимости. d- расчетные графики распределенных приращений нагрузок по длине образующей и дуговой координате панели и перемещений по средней образующей панели

Видно, что при одинаковых приращениях давления q знак меняется на противоположенной после превышения прогибов панели хорды ее дуги.