ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИХ СВОЙСТВ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ И МЕТАЛЛАХ

Лабораторная работа № 3

ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИХ СВОЙСТВ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ И МЕТАЛЛАХ

Химический потенциал невырожденного идеального газа. Энергия Ферми.

Химический потенциал определяет среднюю энергию частиц в термодинамической системе микрочастиц, отнесенную к одной части-це. Для химического потенциала можно записать:

(1)

С другой стороны, количество частиц в термодинамической сис-теме определяется интегрированием полной функции распределения:

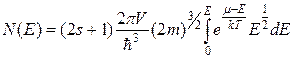. (2)

Дифференцируя это выражение по энергии, получим:

. (3)

В равновесном состоянии энергия и количество частиц в термо-динамической системе постоянны, поэтому для такого состояния мож-но записать . Учитывая это соотношение, получим:

(4)

Воспользовавшись формулой Больцмана

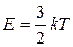(5)

и обозначив концентрацию частиц , получим:

(6)

Логарифмируя это выражение, получим выражение для химиче-ского потенциала:

. (7)

Величина

(8)

получила название эффективного числа состояний. Подставляя это выражение в химический потенциал, получим:

(9)

Химический потенциал в применении к полупроводникам и ме-таллам определяет среднюю энергию электронного газа, отнесенную к одному электрону, и совпадает с понятием энергии Ферми.

Распределение Ферми-Дирака при абсолютном нуле

Электроны в металле можно рассматривать как находящиеся в потенциальной яме. Выход электронов из металла требует затраты энергии для преодоления сил химической связи, которые удерживают электроны. Обычно за нулевой уровень энергии принимается поверх-ность металла – электроны, находящиеся вне металла. В связи с этим электроны в металле, находящиеся в потенциальной яме, имеют отри-цательную энергию.

Рис.1. Электроны в потенциальной яме

Если бы электроны не были фермионами, то при абсолютном ну-ле они бы скапливались на дне потенциальной ямы. Являясь фермио-нами и подчиняясь принципу запрета Паули, электроны последова-тельно занимают уровни от дна потенциальной ямы до верхнего по-следнего уровня, который получил название уровня Ферми. Энергия этого уровня соответствует энергии Ферми. Поскольку энергияФерми, в этом случае отсчитывается от дна потенциальной ямы, то эта энер-гия всегда положительная.

Рассматривая заполнение энергетических уровней при абсолют-ном нуле, следует отметить, что при E<E_F все энергетические уровни будут заняты. В то же время для E>E_F все энергетические уровни бу-дут свободны. Таким образом, для функции распределения Ферми-Дирака при абсолютном нуле можно записать:

Полная функция распределения Ферми-Дирака запишется:

Вычисление энергии Ферми

Энергия Ферми E_F может быть найдена интегрированием полной функции распределения в пределах от 0 до E_F:

. (10)

Этот интеграл определяет число частиц с энергией E_F. Полная функция распределения для вырожденного газа фермионов при темпе-ратуре абсолютного нуля будет определяться:

.

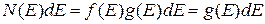Плотность числа состояний определяется:

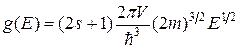. (11)

Интегрируя, получим полное число частиц:

. (12)

Учитывая, что спин электрона равен s=1/2 и вычисляя интеграл, получим:

. (13)

Из этого выражения энергия Ферми при температуре абсолют-ного нуля определяется:

. (14)

Статистика носителей заряда в примесных полупроводниках

N-типа

Зонная диаграмма примесного полупроводника n-типа имеет вид:

Рис. 7. Зонная диаграмма полупроводника n-типа

К статистическим параметрам примесного полупроводника n-ти-па относятся виды носителей заряда, их концентрации и функции рас-пределения, энергия газа, формируемого этими зарядами.

В примесном полупроводнике n-типа существуют основные носи-тели заряда – электроны (n_n) и неосновные носители заряда – дырки (p_n). Концентрация основных носителей заряда определяется наличи-ем донорной примеси n_d и собственной проводимостью полупровод-ника n_i. Концентрация основных носителей заряда в примесном полу-проводнике может, практически, принимать любые значения. Это определяется легированием полупроводника донорной примесью. По-этому электронный газ в полупроводнике n-типа может опреде- ляться как статистикой Максвелла-Больцмана, так и статистикой Ферми-Дирака.

Концентрация неосновных носителей заряда p_n определяется соб-ственной проводимостью примесного полупроводника p_n=p_i. Поэтому дырочный газ в примесном полупроводнике n-типа будет определять-ся статистикой Максвелла-Больцмана.

Для определения концентраций носителей заряда воспользуемся интегральной функцией распределения:

.

В случае неосновных носителей заряда функция распределения f(E) определится:

.

Плотность числа состояний запишется:

,

.

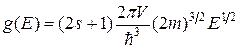Из этих выражений концентрация неосновных носителей заряда определится:

.

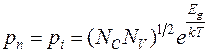Концентрация основных носителей заряда будет определяться:

,

,

где величина n_d будет зависеть от концентрации донорной примеси N_d. Если концентрация донорной примеси будет меньше эффективно-го числа состояний в зоне проводимости N_d<N_c, то при определении n_d необходимо воспользоваться статистикой Максвелла-Больцмана:

,

где E_d – энергия ионизации донорного уровня. В том случае, если кон-центрация донорной примеси соизмерима с эффективным числом со-стояний в зоне проводимости N_d~N_c, то при определении n_d необходи-мо воспользоваться распределением Ферми-Дирака:

,

где химический потенциал определится:

,

.

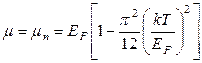Таким образом для определения концентрации основных носите-лей заряда, связанных с донорной примесью, необходимо рассмотреть систему нелинейных уравнений, включая интегральное уравнение.

Библиографический список

1. Епифанов, И. П. Физические основы микроэлектроники/ И. П. Епифанов.– М. : Высшая школа, 1983.

2. Епифанов, И. П. Твердотельная электроника/ И. П. Епифанов. – М. : Высшая школа, 1986.

3. Аваев, Н. А. Основы микроэлектроника/ Н. А. Аваев. – М.: Радио и связь, 1991.

4. Волков, В. М. Микроэлектроника/ В. М. Волков. – Киев: Техника, 1983.

Лабораторная работа № 3

ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИХ СВОЙСТВ НОСИТЕЛЕЙ ЗАРЯДА В ПОЛУПРОВОДНИКАХ И МЕТАЛЛАХ