Поиск экстремума целевой функции

Если целевая функция нелинейна, то поиск оптимального режима работы ТО производится, чаще всего, градиентными методами,применение которых позволяет решить практически любую задачу нелинейной оптимизации. Сущность градиентных методов заключается в том, что на каждом шаге оптимизации при поиске максимума или минимума целевой функции приращения управляющих параметров выбираются пропорциональными частным производным целевой функции по этим параметрам.

Это правило можно отобразить с помощью следующего рекуррентного соотношения:

, (4.18)

где – значение i-го параметра на (j+1)-м шаге оптимизации;

– значение того же параметра на j-том шаге оптимизации;

– коэффициент, определяющий величину шага оптимизационной процедуры, называемый также шагом;

– частная производная целевой функции F_ц по i-му параметру x_i, которая вычисляется на каждом шаге оптимизации;

n – количество управляющих параметров оптимизируемого процесса.

Частные производные являются проекциями градиента функции F_цв (n+1)-мерном пространстве, которое составляют параметры x_i и функция F_ц. Примем во внимание, что градиент – это вектор, указывающий направление на максимум функции. По этой причине знак плюс в формуле (4.18) ставится, если оптимальный режим соответствует максимуму целевой функции, а знак минус, если оптимальный режим соответствует минимуму целевой функции.

В пределах шага оптимизационной процедуры, когда оптимизируемые параметры получают приращения

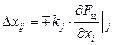
, (4.18′)

расчётные значения частных производных не изменяются. После выполнения шага оптимизации значение , согласно соотношению (4.18), увеличивается или уменьшается до значения , а это означает, что при изменении параметров техпроцесса в пределах ÷ , i = 1, 2,…n, значения частных производных функции F_цпо этим параметрам принимались неизменными. Следовательно, на каждом шаге оптимизации, в пределах шага, целевая функция принимается линейной, хотя в действительности она нелинейна. Если шаг чрезмерно велик (значение чрезмерно велико), то в пределах шага фактические значения частных производных функции F_цмогут уменьшиться до нуля и даже изменить свой знак, а последнее будет означать, что система управления «проскочила» точку оптимального режима, точку, в которой все частные производные целевой функции равны нулю, т.е.

= 0, i = 1, 2,…n. (4.19)

На следующем шаге при чрезмерно большом система управления может опять пройти точку оптимального режима, но уже в обратном направлении. Начнется так называемое рысканье, из-за которого оптимальный режим не будет достигнут. Если значение достаточно мало, то рысканья не будет, но при чрезмерно малом продвижение к оптимальному режиму будет замедленным, из-за чего оптимальный режим также не будет достигнут: во-первых, поиск оптимального режима может затянуться на всё время реализации техпроцесса (даже при неизменности его параметров); во-вторых, за время поиска параметры техпроцесса могут изменяться так быстро, что система управления не будет успевать найти управляющие параметры, соответствующие оптимальному режиму. Дело в том, что при динамической оптимизации, производимой в течение работы ТО, значения частных производных целевой функции должны быть определены экспериментально, методом конечных разностей. Если контролируются n параметров, то на каждом шаге оптимизации, одновременно с выполнением технологической задачи, необходимо произвести поочередно малое приращение каждого из параметров 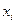(i = 1, 2,…n). Эти приращения должны быть достаточно малы, с тем чтобы не нарушать достигнутый уровень оптимизации режима работы, а с другой стороны – достаточно велики, чтобы их можно было измерить с заданной точностью с помощью существующей приборной базы. Кроме того, данные приращения должны оставаться неизменными в течение серии шагов оптимизации, чтобы уменьшить объём производимых при поиске оптимального режима вычислений.

Допустим, что установлены оптимизированные значения управляющих параметров (i = 1, 2,…n) на j-том шаге оптимизации. Им соответствует исходное на текущем шаге оптимизации значение целевой функции F_ц0. Далее следует последовательно, одно за другим, выставить значения управляющих параметров +Δ 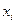, где Δ 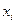– запланированное пробное приращение i-того параметра, и вычислить n новых значений целевой функции F_цi (i=1, 2,…n), соответствующих текущему шагу оптимизации. После этого можно будетвычислить все необходимые для реализации очередного шага оптимизации значения n частных производных целевой функции:

= , i=1, 2,…n. (4.20)

Новые оптимизированные значения x_{ij +1} на (j+1)-м шаге оптимизации рассчитываются по формуле (4.18), после чего рассчитывается новое значение F_ц0.

Рассмотренная процедура измерений и расчетов может оказаться достаточно длительной при управлении реальным быстротекущим технологическим процессом, и тогда она, как показано выше, не гарантирует оптимальности режима работы из-за возможного рысканья или недостаточности быстродействия. Если же система управления достаточно быстродействующая, то итерационный процесс поиска оптимального режима должен продолжаться до тех пор, пока не получится

|F_цi – F_цo| < ε, i=1, 2,…n,(4.21)

где ε– малое положительное число, выбранное так, чтобы неравенство (4.21) обеспечивало достаточную близость к оптимальному режиму, т.е. к выполнению условий (4.19).

При поиске оптимального режима в точке экстремума целевой функции необходимо следить за тем, чтобы этот экстремум был глобальным, а не локальным, т.е. чтобы он соответствовал точке наибольшего значения целевой функции из всех значений, которых она достигает в точках локальных экстремумов. Эта проблема решается на этапе выбора начальной точки задания рабочего режима, которая должна находиться в такой окрестности глобального оптимума, что дальнейший поиск оптимального режима методом градиента автоматически приводил бы именно к глобальному оптимуму. Выбор такой начальной точки, т.е. совокупности управляющих параметров, задающих исходный рабочий режим, предшествующий автоматическому поиску оптимального режима, зависит в значительной степени от опыта и интуиции проектировщиков и наладчиков системы оптимизации.

Далее необходимо обеспечить максимальное быстродействие системы оптимизации без чрезмерного рысканья в окрестности точки оптимального режима. При этом следует учитывать, что наибольшее время в течение шага оптимизации затрачивается на сбор экспериментальных данных для расчета проекций градиента целевой функции в соответствии с соотношением (4.20). Чтобы наиболее эффективно использовать полученный экспериментальный материал, следует правильно выбрать значение шагового коэффициента . Начальное его значение выбирается исходя из опыта проектирования и наладки аналогичных систем автоматической оптимизации. Наиболее простым способом уточнения значений является метод удвоения длины шага. Он заключается в том, что если после выполнения шага оптимизации с начальным значением окажется F_ц< F_цo (при минимизации F_ц) или F_ц > F_цo ( при максимизации F_ц), то производится еще один шаг без сбора экспериментальных данных, с прежними значениям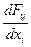и и , что эквивалентно удвоению . Если после этого значение F_ц снова уменьшится (при минимизации) или увеличится (при максимизации), то приступают к обычному шагу оптимизации, т. е. начинают сбор экспериментальных данных но с новым, удвоенным значением . В противном случае попытка удвоения считается неудачной и очередной шаг оптимизации производится с прежним значением . Если же на очередном шаге оптимизации сразу окажется F_ц>F_цо (при минимизации) или F_ц<F_цо при максимизации, то следующий шаг производится обычным порядком, но с уменьшенным вдвое значением . Тем самым предотвращается рысканье.

Значения могут быть уточнены и расчётным путём, например – методом одномерной минимизации (или максимизации). Тогда они на каждом шаге оптимизации определяются исходя из условия минимальности или, соответственно – максимальности функции

(4.22)

Здесь функция φ_ц трактуется как функция одного лишь параметра . Так получается, когда в формулу для F_ц подставляют, вместо каждого x_i, его конкретное значение, полученное на j-том шаге оптимизации, в виде

x_ij+·k_j ∂F_ц/∂x_ij ,

причем значение k_j считается неизвестным. Далее, исходя из уравнения

dφ_ц/dk_j=0,

определяется значение , соответствующее минимуму (при минимизации) или максимуму (при максимизации) функции φ_ц в заданной точке x_ij. Если оптимизация проводится в соответствии с соотношением (4.18), а значение при этом определяется исходя из минимума φ_ц, то такой метод оптимизации называют методом наискорейшего спуска. Имеется в виду скорейший спуск к точке минимума целевой функции, но этот термин применяется и при поиске оптимального режима в точке максимума целевой функции.

Уточнение значений может производиться либо экспериментально, скажем – методом удвоения длины шага, либо аналитически, с использованием математической модели техпроцесса. В первом случае процедура удвоения длины шага требует дополнительного экспериментального определения значения F_ц после удвоения шага, что ведет к увеличению времени уточнения , но дополнительные расчёты, которые также требуют времени, при этом не нужны. Использование модели техпроцесса, необходимое для уточнения k_j аналитическим путём, скажем, методом одномерной оптимизации, позволяет избежать дополнительного сбора экспериментальных данных, но объём расчётов при этом многократно возрастает.