Поиск предельно допустимого оптимального режима

Зачастую нужный экстремум целевой функции не может быть достигнут из-за имеющихся технологических ограничений. Тогда оптимальный режим реализуется в одной из граничных точек области допустимых значений параметров техпроцесса. Если ограничения будут заданы в виде линейных неравенств, то напрашивается применение приёма линеаризации целевой функции, присущей методу градиента, в окрестности оптимального режима для сведения решения исходной задачи к линейному программированию.

Целевая функция F_ц после линеаризации принимает вид:

. (4.30)

Исходя из выражения (4.30) и уравнений линейных ограничений, находят точку оптимального режима x_оптл для линеаризованных условий задачи путём линейного программирования, например, симплексным методом, описанным в § 4.3. Полученная точка x_отплне будет, скорее всего, точкой искомого оптимального режима, так как исходная целевая функция F_ц является в действительности нелинейной. Истинная оптимальная точка будет находиться у вогнутых функций ближе к исходной рабочей точке x_o=(x_1o, x_2o, … ,x_no), а у выпуклых – дальше от неё.

Поэтому новую рабочую точку находят исходя из соотношения

, (4.31)

где λ – коэффициент пропорциональности, определяющий величину шага вычислений.

Величину λ (обычно 0 ≤ λ ≤ 1) можно определить с помощью процедуры удвоения шага, но лучше начинать с половинного шага, т. е. сначала положить λ=1/2, а далее ополовинивать или удваивать шаг до тех пор, пока значение F_ц будет изменяться в нужную сторону. Можно также пользоваться приёмами одномерной минимизации (максимизации). После определения значения λ вычисляют координаты точки x и соответствующее им значение F_ц, которое на первом шаге оптимизации будет, скорее всего, недостаточно близким к оптимальному значению. Если это так, то придётся опять определить проекции градиента от F_ц, составить, согласно (4.30), новое значение F_цл и приступить к новому шагу оптимизации, начиная с линейного программирования.

Более универсален метод штрафных функций, при применении которого не требуется соблюдение линейности уравнений ограничений. Применение этого метода рассмотрим на примере определения максимального значения вогнутой целевой функции F_ц(x), x=(x₁, x₂, … , x_n) при условиях

g_i(x)≤b_i (i=1, 2, … ,m), x_j≥0 (j=1, 2, … , n),

где g_i(x) – линейные или нелинейные выпуклые функции.

Для решения данной задачи формируют штрафную функцию, которая чаще всего имеет вид

, (4.32)

,

а a_i>0 – весовые коэффициенты.

Далее, вместо непосредственного решения заданной задачи, находят максимальное значение функции

с помощью рекуррентного соотношения

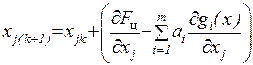k_k , (4.33)

причём фигурирующие в соотношении (4.33) частные производные относятся к k-тому шагу оптимизации.

Из (4.33) следует, что если значение x_jk находится в пределах допустимых решений исходной задачи, то второе слагаемое в скобках равно нулю (a_i=0) и процесс решения идёт обычным методом градиента, ср. с соотношением (4.18). Если же данная точка не принадлежит области допустимых решений, то за счёт второго слагаемого в скобках на последующих итерациях достигается возвращение в область допустимых решений.

Заметим, что динамическая оптимизация в процессе функционирования ТО проводится в условиях задания необходимых ограничений режима работы ТО независимо от ведущегося поиска оптимального режима и с приоритетом над ним. В результате, система управления ТО не выполняет указаний по оптимизации режима работы, если эти указания выходят за рамки запрограммированных ограничений. В качестве примера можно привести токоограничение и ограничение скорости вращения двигателя в электроприводах, запрограммированные независимо от поиска оптимального режима. В этих условиях нет необходимости усложнять алгоритм поиска режима введением ограничивающих условий. Сложные алгоритмы автоматической оптимизации типа метода штрафных функций используются лишь тогда, когда более простые способы введения ограничений режима работы ТО неэффективны. С другой стороны, динамическая оптимизация быстротекущих процессов, в отличие от статической, не прекращается даже в случае достижения точки оптимального режима ввиду постоянных, непрерывно возникающих отклонений от него. Оптимизация техпроцесса в течение его реализации ведется поэтому непрерывно, с высокой периодичностью.