Синтез нечеткого регулятора положения

Типичным режимом работы следящих электроприводов СПУ является позиционирование с обеспечением точного останова в заданной точке. Подход к точке останова может осуществляться при различных нагрузках, что приводит к потере точности при статическом регуляторе положения или к затягиванию процесса останова при наличии астатического регулятора. Противодействовать данному явлению можно с помощью нечеткого регулятора положения (НРП), предназначенного для оптимизации режима позиционирования следящего электропривода, структурная схема которого приведена на рис. 4.5.

Рис. 4.5. Структурная схема следящего электропривода с нечетким регулятором положения:

УМК- управляющий микроконтроллер;

РП- регулятор положения в составе основного регулятора (ОРП) и нечеткого регулятора (НРП) ;

КСД- контур скорости электродвигателя;

МП- механическая передача.

Здесь микроконтроллер УМК управляет контуром КСД скорости ω двигателя посредством управляющего напряжения Uзс. Контур скорости может быть реализован комплектным электроприводом постоянного или переменного тока. Настройка КСД на модульный оптимум позволяет отобразить его инерционным звеном с постоянной времени Т_с, а К_ос –это коэффициент обратной связи по скорости двигателя в контуре скорости. Двигатель приводит в движение рабочий орган через механическую передачуМП с коэффициентом передачи К_мп. Сигнал обратной связи по положению S рабочего органа подается на вход следящей системы через датчик обратной связи по положению с коэффициентом передачи К_оп. Данный сигнал используется также для формирования обратной связи по скорости перемещения рабочего органа с помощью дифференцирующего звена с постоянной времени Т_д.

Значение рассогласования

= S_з - K_onS (4.39)

между заданным положением (уставкой положения) S_з и сигналом обратной связи по положению K_onS подается как на основной регулятор положения ОРП, так и на нечеткий регулятор положения НРП, а на НРП кроме того подается сигнал обратной связи по скорости рабочего органа, взятый с обратным знаком. Учитывая, что производная по времени равна (при S_з= const)

,

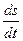приходим к выводу, что на вход НРП подается сигнал , равный

ε = δ + T_д . (4.40)

Будем далее именовать величину ошибкой по положению, а величину d /dt – производной ошибки по положению

Из структурной схемы рис. 4.5 получаем следующее дифференциальное уравнение непрерывной части данного следящего привода:

-U_зс = Т_сТ_в T_в , (4.41)

где

Т_в= 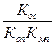– (4.42)

эквивалентный коэффициент вязкого трения, численно равный обратной величине коэффициента усиления разомкнутого контура непрерывной части привода;

U_зс - управляющее напряжение, формируемое на выходе РП.

Значение U_зс при управлении от НРП изменяется дискретно. Полагаем, что при >0 имеет место U_зс =U_змакс, при <0 имеем U_зс =-U_змакс, а при малых значениях < , соответствующих зоне нечувствительности РП, должно быть U_зс= 0.

Полагаем y= и, с учетом того, что

,

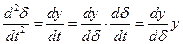записываем дифференциальное уравнение фазовых траекторий рассматриваемого привода в виде

Интегрируя полученное уравнение, придем к следующему уравнению фазовых траекторий:

T_c(y-y_o)+U_зс , (4.43)

где y_o, - начальные значения фазовых переменных при интегрировании.

При U_зс= 0 получим

Т_с(y-y_o)=-( ), (4.43’)

т.е. фазовые характеристики являются при U_зс = 0 прямыми с отрицательным наклоном . Это означает, что при U_зс = 0 происходит торможение привода. Если при y=0 окажется что U_зс = 0, то наступит состояние останова (δ = const), так как отсутствует побудительная причина дальнейшего изменения скорости (U_зс = 0), а последняя стала равной нулю (y= 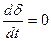). С другой стороны, перерегулирование по скорости невозможно, так как контур скорости КСД (см.рис.4.5) эквивалентен апериодическому звену.

Далее будем полагать, что зона нечувствительности релейного НРП определяется заданной точностью позиционирования и составляет δ_гр = .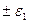

В таком случае условиями переключения из режимов U_зс ≠0 в режим U_зс=0 и обратно будут, согласно (4.40) уравнения

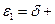T_дy;

T_дy. (4.44)

Определим максимальное (граничное) значение y_гр, которое при переходе к режиму U_зс=0 обеспечивает уменьшение скорости до значения y=0 при . Поскольку уравнения (4.44) симметричны, достаточно рассмотреть случай, когда имеем конечное значение при конечном значении y=0. Соотношение между начальными значениями y_o=y_гр и в этом случае будет определяться вторым уравнением (4.44), откуда найдем

_дy_гр).

Подставив последнее соотношение в (4.43’) при y=0, y_o=y_гр и δ = ε₁, получим (с учетом симметрии параметров)

y_гр= .(4.45)

При Т_д→T_с имеем y_гр→± ∞,так что при Т_д ≥ Т_с всегда обеспечивается устойчивый останов привода в пределах заданной зоны _1. Однако оптимальный по быстродействию (скользящий) режим работы следящего электропривода с релейным управлением реализуется лишь при Т_д < Т_с. При работе в скользящем режиме фазовая траектория привода проходит вдоль линий переключения (4.44), отклоняясь от них на величину гистерезиса релейной характеристики РП, который незначителен. Поэтому найдем зависимость от параметров привода максимально допустимого значения U_зс, обеспечивающего выход на переключение от >0 к U_зс=0 при условии ,что

<y< , Т_д<Т_с.

Отсюда найдем условия, при которых обеспечивается устойчивый останов в заданной точке позиционирования, причем внутри зоны нечувствительности.

Полагаем, U_зс>0, откуда следует, что движение в сторону уменьшения начнется при >0 и y_о=0.

При U_зс<0 начальное значение будет противоположным по знаку, а в остальном расчетные соотношения будут такими же. Движение при U_зс>0, будет продолжаться до границы, определяемой первым уравнением (4.44), откуда получим условие переключения на работу с U_зс=0 в интересующем нас граничном режиме:

=ε₁ – T_дy_гр.

Подставив полученное значение при y_о=0 и y=y_гр в уравнение (4.43), получим

Т_сy_гр - U_зс ln(1+ )=T_дy_гр - .

Теперь необходимо подставить в полученное уравнение значение y_гр из соотношения (4.45) в варианте со знаком минус; поскольку имеем Т_д< Т_с, а при U_зс>0 и при работе в скользящем режиме имеет место y<0. После подстановки получим:

. (4.46)

Из полученного уравнения (4.46) следует, что при

׀U_зс׀< , Т_д<Т_с, (4.47)

обеспечивается устойчивое завершение позиционирования в пределах независимо от величины начального рассогласования . Последнее же перед остановом не может превышать значение более чем на ширину зоны гистерезиса ,т.е. перед остановом имеет место .

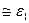Полученные соотношения используем в алгоритме построения нечеткого релейного регулятора положения. Так, величину будем рассчитывать по формуле (4.40). Если и достигнута граница области функционирования нечеткого регулятора (δ<δ_гр), то устанавливаем U_зс= U_зсмакс, а если , то устанавливаем U_зс= -U_зсмакс. При достижении значения пределов , устанавливаем U_зс=0. Одновременно задаем пониженное значение U_зс, определенное с помощью формулы(4.47) и уточненное при настройке регулятора. Таким образом, подход к заданному положению будет осуществлен с максимальной скоростью, а предотвращение колебаний у заданного положения будет осуществлено после достижения заданной зоны останова ( зоны нечувствительности). На этом функции НРП должны заканчиваться. При поступлении большого возмущения, когда , где δ_гр- граничное значение ошибки, определяющее пределы функционирования НРП, нечеткий регулятор должен быть автоматически отключен, а вместо него должен быть включен ОРП.

Необходимость в нечетком регуляторе возникла потому, что при подходе к заданному положению величина измеряется малым количеством дискрет (отсчетов) датчика положения , а каждая дискрета занимает относительно соседней дискреты не вполне определенное положение из-за погрешности шкалы датчика. Деления шкалы устанавливаются с некоторой погрешностью, которая при переходе от дискреты к дискрете изменяется, так как имеет случайный характер. При большом количестве отсчетов погрешности отдельных дискрет взаимно компенсируются, но при подходе к заданному положению, когда речь идет о значениях , равных 1-2 дискретам, ,погрешность может оказаться значительной, близкой к величине одной дискреты. Распределение погрешностей отсчета положения рабочего органа можно отобразить в виде совокупности нечетких множеств

А_δ={µ },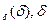

функции принадлежности которых приведены на рис.4.6. Величина здесь отложена по оси абсцисс в дискретах, приведенных ко входу РП в соответствии с соотношением (4.39). Распределение функции принадлежности µ на каждой дискрете соответствует равномерному убыванию возможности предполагаемого расположения дискреты в обе стороны от заданной позиции , которой соответствует µ =1, до крайних позиций ±1. Предполагается, что максимальная погрешность по положению не превышает одной дискреты. На рис. 4.6.заштрихована область функции принадлежности дискреты .

Рис.4.6. Функции принадлежности дискрет ошибки по положению рабочего органа

Видно, что помимо заданной позиции линия дискреты может быть случайным образом расположена с убывающей вероятностью от позиции до позиции . Функции µ_y принадлежности величины Т_д , второй составляющей сигнала , подаваемого на вход НРП, задаются по тем же правилам , что и µ_δ. Они отображают множества

А_y={µ_y (Т_д ,Т_д }.

Величина сигнала , являющаяся, согласно соотношению(4.40), суммой двух нечетких чисел, также является нечетким числом. Нас будут интересовать реализации , соответствующие реализациям и Т_д , поступающим на вход НРП. Их можно получить по правилам сложения нечетких чисел, рассмотренным выше (см.§ 4.5.1.).

При сложении нечетких чисел значения треугольной функции принадлежности удобно рассчитывать по формуле

µ_i=1-| -i|, (4.48)

где и_i – значение носителя i- того нечеткого множества;

а – величина дискреты носителя нечеткого множества.

В рассматриваемом случае имеем а=1. При i =2 заштрихованное нечеткое множество на рис.4.6 имеет µ_i=1 при и_i=2, µ_i=0 при и_i=1 и при и_i=3. В каждом нечетком множестве имеем

i-1≤ и_i≤ i+1.

Допустим, в качестве примера, что =1,7 и Т_д =-0,9 (при работе в скользящем режиме значения и имеют противоположные знаки). Носитель =1,7 принадлежит одновременно множествам 1 и 2, а носитель Т_д =-0,9 – множествам -1 и 0. Отсюда, с помощью формулы (4.48), полагая а=1 и и_i=1,7 или и_i= -0,9, получаем следующие реализации нечетких чисел А_δ и А_y:

А_δ1= , А_δ2= ; А_y(-1)= 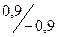, А_y0= .

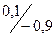При вычислении значения в соответствии с формулой (4.40) носители А_δ поочередно складываются с носителями А_y и каждой сумме присваивается минимальное значение функции принадлежности слагаемых, см. (4.38). Получим следующий ряд:

А_δ + А_y= { },

причем повторяющееся значение записываем только один раз. За истинное значение суммы принимаем, согласно максиминному принципу обобщения,

А_δ + А_y = ,

что соответствует значению сигнала управления

·0,8=0,56.

Если величина больше единицы, то значение следует вычислять по формуле

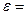а(i)+∆а·µ_а,

где а(i)- целая часть значения ;

∆а- дробная часть;

µ_а- функция принадлежности , вычисленная по вышеизложенной методике.

Для вычисления Т_д рекомендуем использовать разностную формулу

Т_д = , (4.49)

где Т – время цикла управления;

δ₁ иδ₂ – значения в начале и в конце цикла.

Значения вычисляются по формуле (4.39) с учетом нечеткости S.

Контрольные вопросы к главе 4

1. Перечислите основные направления решения задачи оптимизации функционирования ТО.

2. Каково назначение алгоритмов управления и их классификация?

3. Каковы разновидности и порядок функционирования алгоритмов стабилизации?

4. Как действуют внутренние и внешние возмущения в многосвязных (многомерных) системах управления?

5. Что такое инвариантная ( к какому-либо возмущению) система управления?

6. Сформулируйте условия инвариантности управляемых параметров ТО, заданных системой линейных уравнений.

7. Как компенсируются возмущения в инвариантных многосвязных системах?

8. Как и с какой целью вводятся отрицательные обратные связи в отдельных каналах управления?

9. Приведите уравнение i- того канала управления с учетом действия отрицательной обратной связи и объясните его смысл.

10. Сформулируйте понятие статической и динамической оптимизации.

11. Что такое шаг оптимизации?

12. В каких случаях применяется линейное программирование?

13. Сформулируйте основную задачу линейного программирования

14. В каком виде должны быть представлены условия задачи оптимизации для решения ее симплексным методом?

15. Приведите основные положения симплексного метода оптимизации.

16. Опишите методику нахождения точки оптимального режима путем построения многоугольника решений, если целевая функция является линейной .функцией двух переменных.

17. Перечислите признаки оптимальности опорного плана при оптимизации симплексным методом.

18. Объясните порядок составления исходной расчетной таблицы при оптимизации симплексным методом.

19. Объясните порядок улучшения опорного плана путем замены одного из векторов базиса на один из векторов a_j, не входящих в состав базиса.

20. Приведите расчетные формулы для нахождения улучшенного опорного плана при оптимизации симплексным методом.

21. В чем заключается сущность градиентных методов?

22. Какие проблемы решаются при выборе величины шага при оптимизации методом градиента?

23. Каков признак достижения оптимального режима при оптимизации методом градиента?

24. Какова методика определения значений частных производных при оптимизации методом градиента?

25. Как подбирается значение шагового коэффициента k_j методом удвоения длины шага?

26. В чем заключается метод одномерной минимизации (максимизации), как он связан с методом наискорейшего спуска?

27. Как используется метод градиента при оптимизации электрохимической обработки (ЭХО)?

28. Как используется полнофакторный эксперимент на каждом шаге оптимизации ЭХО?

29. Как ведется поиск допустимого оптимального режима при линейности ограничений параметров техпроцесса?

30. Как ведется поиск допустимого оптимального режима методом штрафных функций?