
Главная Случайная страница
Категории:
ДомЗдоровьеЗоологияРнформатикаРскусствоРскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиРкологияРРєРѕРЅРѕРјРёРєР°Рлектроника
Прикладное ПО, применяемое для решения СЛАУ
Для автоматизации расчета систем линейных алгебраических уравнений существуют большое количество программ, например математический пакет MathCad, табличный процессор MS Excel и др.
Когда информация может быть представлена в табличном виде, Microsoft Office Excel является незаменимым помощником. Любой пользователь, знающий возможности табличного процессора Excel, всегда может найти ему применение в своей работе.
Excel имеет огромные возможности Рё, несомненно, является РѕРґРЅРѕР№ РёР· лучших программ своего класса. Большую роль играет его распространенность. Рта программа установлена сегодня практически РЅР° любом компьютере. Получая откуда – либо файлы электронных таблиц, можно быть почти уверенным, что эти документы создавались РІ Excel или, РїРѕ крайней мере, РјРѕРіСѓС‚ быть прочитаны РІ нем. Рменно поэтому умение использовать Excel является очень важным.
С помощью Excel можно создавать, редактировать и печатать красиво оформленные таблицы.
Благодаря встроенным РІ него математическим Рё логическим функциям, можно быстро Рё точно выполнить математические расчеты, РІ том числе РїСЂРё решении систем линейных алгебраических уравнений. Так РїСЂРё использовании матричного метода решения СЛАУ используются функции работы СЃ матрицами РњРЈРњРќРћР–(), Рё МОБР(). РџСЂРё решении СЛАУ методом простой итерации можно использовать логическую функцию ЕСЛР() для организации условия окончания итерационного процесса.
РџСЂРё решении технических Рё инженерных задач РІ приложениях MS Office очень часто приходится применять различные элементы программирования для РёС… автоматизации. Рто предполагает использование различных компонентов языка VBA, макросов Рё РґСЂСѓРіРёС… специальных инструментов.
Visual Basic for Application или сокращенно VBA является реализацией языка программирования Microsoft Visual Basic, встроенной в линейку продуктов Microsoft Office и использующей объективно-ориентированный подход для разработки программ, работающих под управлением операционной системы Windows.
Автоматизация решения СЛАУ
Постановка задачи
Решить систему линейных алгебраических уравнений 2-мя способами: методом Крамера и методом простой итерации с точностью e=0,01
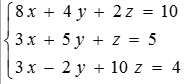
Традиционный способ решения СЛАУ
Решение СЛАУ методом Крамера
1.Запишем исходную матрицу системы.
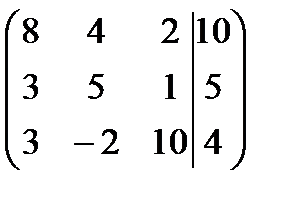
2.Найдем определитель основной матрицы:
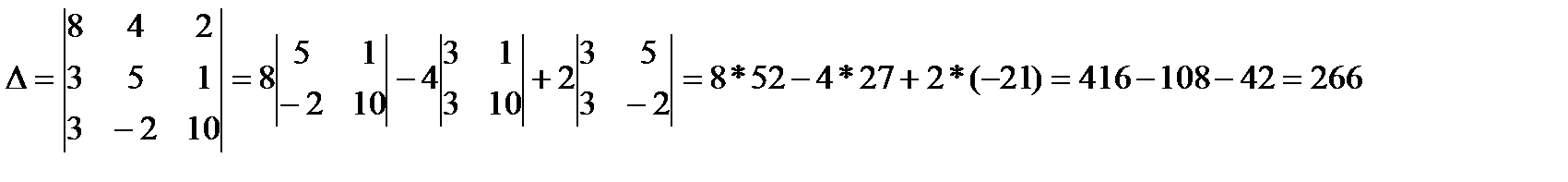 Так как D¹0, то система имеет единственное решение.
Так как D¹0, то система имеет единственное решение.
3.Найдем определители дополнительных матриц, которые получаются из основной путем замены элементов одного из трех столбцов основной матрицы элементами матрицы свободных членов b.
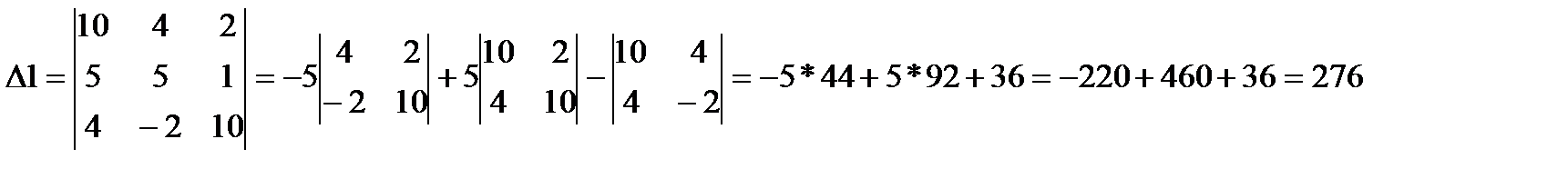
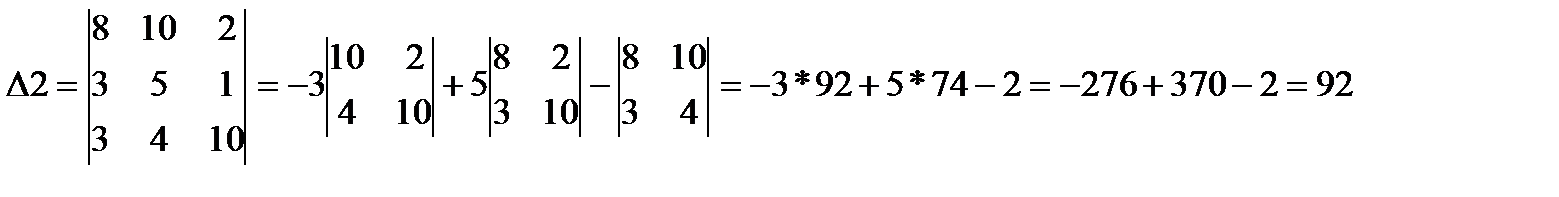
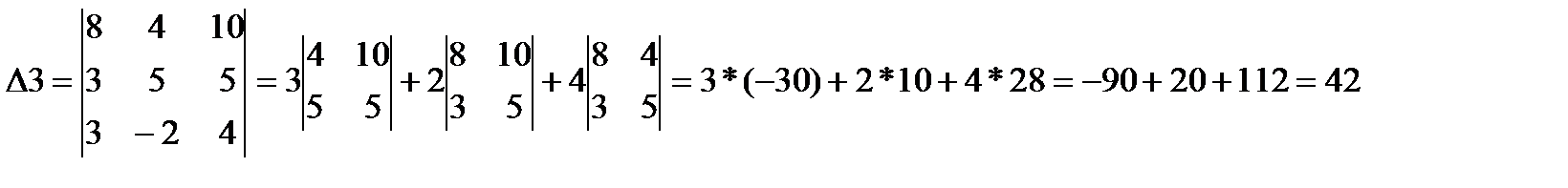
4.Найдем решение системы алгебраических уравнений:
С…1=∆1∕∆=276/266=1,04
С…2=∆2/∆=92/266=0,35
С…3=∆3/∆=42/266=0,16
Решение СЛАУ методом простой итерации
1.Проверяем условия сходимости 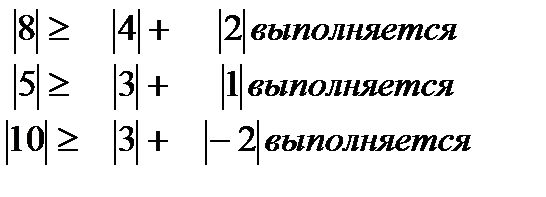
2.Приводим систему к нормальному виду, т.е. из первого уравнения выразим х , из второго у , из третьего z .
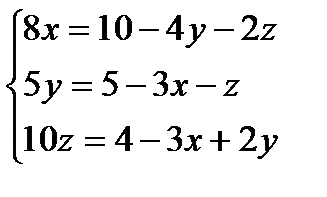
3.Делим первое уравнение на 8,второе - на 5, третье - на 10.
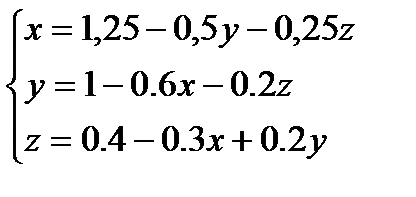
4.Задаем начальное приближение

5.Ртерационный процесс
Я итерация
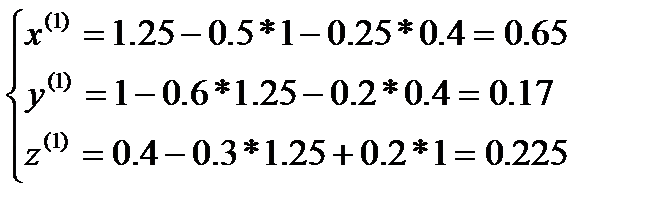

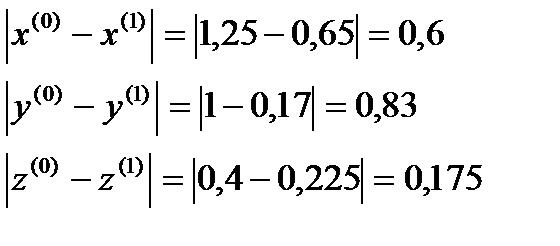
σ=max 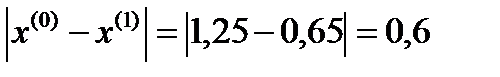 ˃ɛ
˃ɛ
σ=max 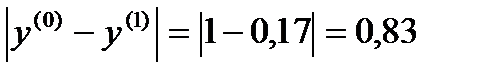 ˃ɛ
˃ɛ
σ=max  ˃ɛ
˃ɛ
Требуемая точность не достигнута
Я итерация
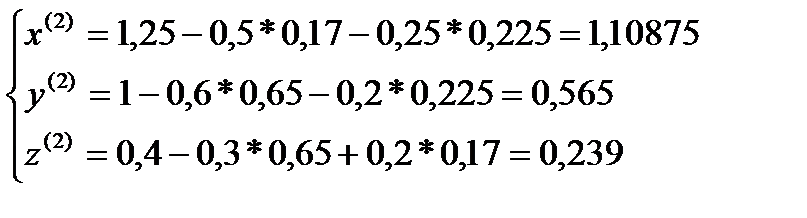
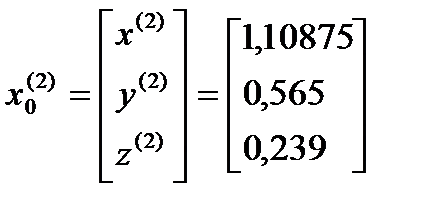
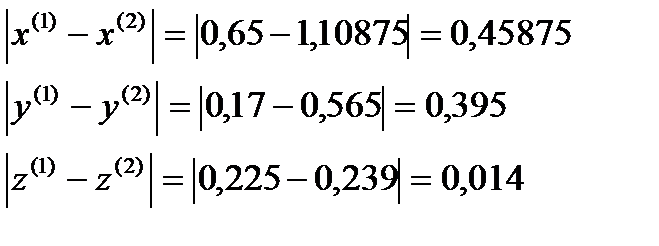
σ=max  ˃ɛ
˃ɛ
σ=max  ˃ɛ
˃ɛ
σ=max 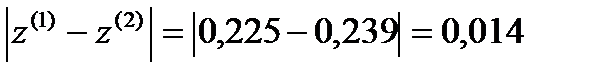 ˃ɛ
˃ɛ
Требуемая точность не достигнута
Я итерация

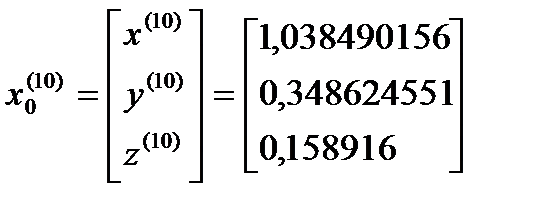
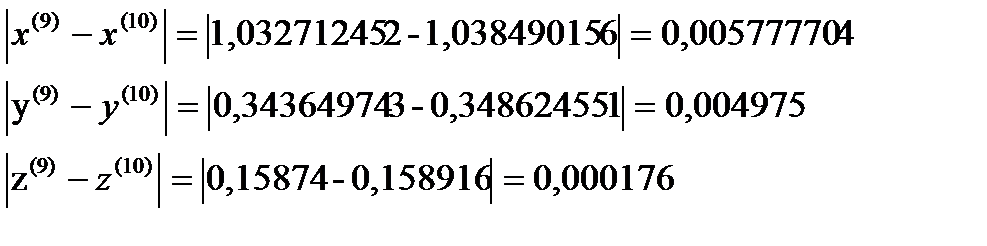
σ=max  ˂ɛ
˂ɛ
σ=max 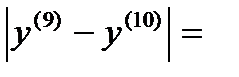
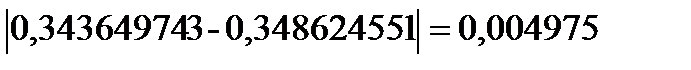 ˂ɛ
˂ɛ
σ=max 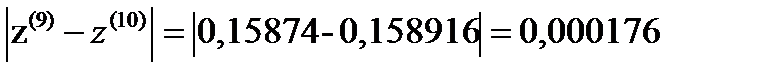 ˂ɛ
˂ɛ
Требуемая точность достигнута
Таким образом,  =
= 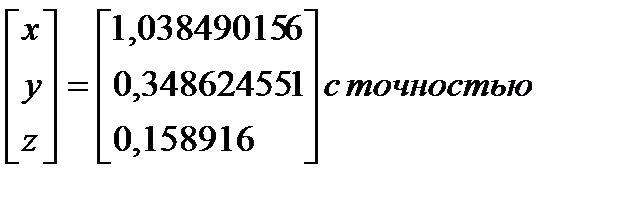 ɛ=0,01
ɛ=0,01
Решение СЛАУ с помощью табличного процессора MS Excel
Решение СЛАУ методом Крамера.
1.Вводим коэффициенты ( 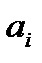 ) и свободные члены системы (
) и свободные члены системы (  ).
).

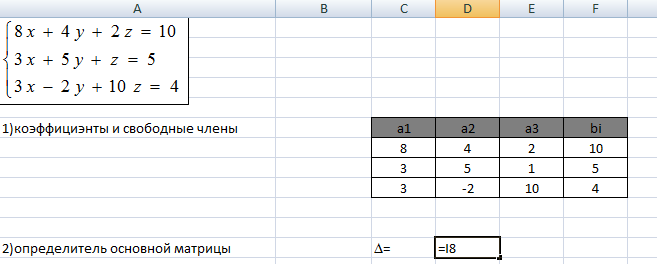
2. РЎ помощью функции ЕСЛРпроанализируем значение определителя РѕСЃРЅРѕРІРЅРѕР№ матрицы. Так как метод Крамера можно использовать для решения систем линейных алгебраических уравнений, Сѓ которых определитель РѕСЃРЅРѕРІРЅРѕР№ матрицы РЅРµ равен 0,то РІ ячейку D12 РІРІРѕРґРёРј формулу =ЕСЛР(МОПРЕД(C7:E9)<>0;МОПРЕД(C7:E9);"использовать РґСЂСѓРіРѕР№ метод решения")
Результаты расчета:
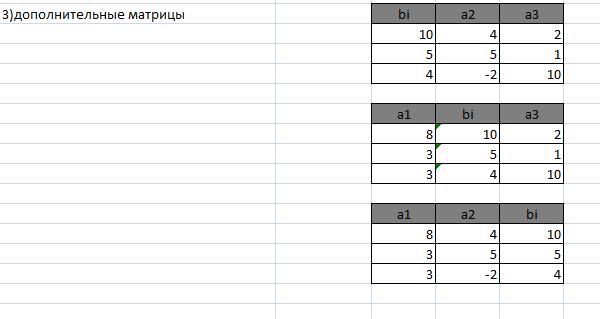
3.Введем дополнительные матрицы системы
Результат:
4.Самостоятельно вычислим определители дополнительных матриц системы с помощью функции МОПРЕД():

5.Вычислим решение системы.



Результат вычислений:

6.Проверка


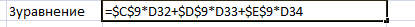
Результат:

Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...