
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Построение корреляционной матрицы и диаграммы рассеяния
1. Создать файл исходных данных (таблица 2).
2. В меню модуля “Основные статистики” выбираем “Correlation matrices”.
 |
Рисунок 38 – Меню модуля “Основные статистики и таблицы”
После выбора этой процедуры откроется диалоговое окно Корреляции Пирсона.
 |
Рисунок 39 - Корреляции Пирсона
Вы можете выбрать переменные как из одного списка (то есть матрица будет квадратной), так и из двух списков (прямоугольная матрица).
В данном примере для простоты выберем все переменные для анализа. Однако следует помнить, что корреляции Пирсона больше подходят для переменных, измеренных в количественных шкалах.
 |
Рисунок 40 - Выбор переменных
Нажмите ОК, чтобы вернуться в диалоговое окно Корреляции Пирсона, где также нажимаем ОКи получаем результат.
 |
Рисунок 41 - Корреляционная матрица
Две остальные опции из диалогового окна Корреляции Пирсонапозволяют получить таблицу данных с коэффициентами корреляции, а также более подробными статистиками (например, р - значение, число пар N, r2 – коэффициент детерминации, t – значения и т.д.).
После того как получена оценка корреляций, посмотрим зависимости на графиках.
Чтобы визуализировать значения корреляций между переменными, можно построить график корреляций. Если щелкнуть по соответствующему коэффициенту корреляции правой кнопкой мыши, то появится меню:
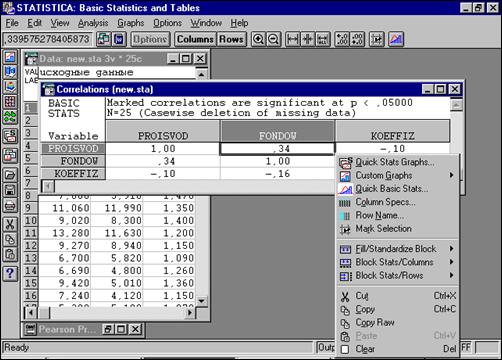 |
Рисунок 42 - Меню “Быстрые статистические графики”
Теперь перейдите в подменю Быстрые статистические графикии выберите Диаг. рассеяния/довер. (Quick Stats Graphs).
Будет построен график с параметрами, заданными по умолчанию (диаграмма рассеяния для выбранного коэффициента корреляции с прямой регрессии, 95% - я доверительная полоса и уравнение регрессии в заголовке).
 |
Рисунок 43 - Меню Построение диаграммы рассеяния для коэффициента корреляции
 |
Рисунок 44 - Диаграмма рассеяния коэффициента корреляции
Опишем некоторые возможности для настройки построенного графика зависимости.
Если вы щелкните где-нибудь на свободном месте снаружи осей графика, появится меню глобальных опций.
 |
Рисунок 45 - Меню глобальных опций
Большинство основных настроек формата графика доступно в диалоговом окне Общая разметка (см. выше первую опцию контекстного меню).
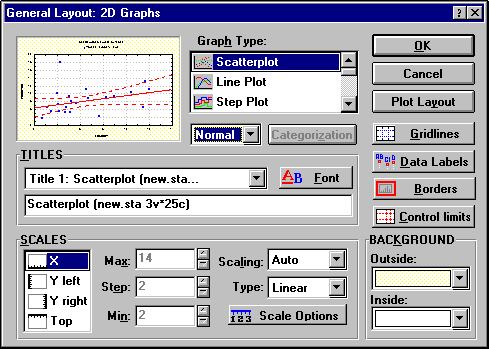 |
Рисунок 46 - Меню “Общая разметка”
Ниже показаны основные соглашения по использованию мыши для настройки графиков.
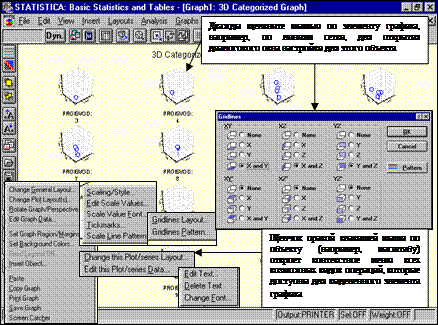

Рисунок 47 – Настройки графиков
2 Множественная регрессия
Шаг 1.Из Переключателя модулей STATISTICA откройте модуль Множественная регрессия – Multiple regression.Высветите название модуля и далее нажмите кнопку Switch to (Переключится в)либо просто дважды щелкните мышью по названию модуля: Multiple regression.
Шаг 2.На экране появится стартовая панель модуля (рис.48):
 |
Рисунок 48 - Стартовая панель модуля Множественная регрессия
Нажмите кнопку Открыть данные (Open Data)и откройте созданный файл данных ***. Далее выберите переменные для анализа. Выбор переменных осуществляется с помощью кнопки Переменные (Variables),находящейся в левом верхнем углу панели.
После того как кнопка будет нажата, диалоговое окно Выбрать списки зависимых и независимых переменных – Select dependent and independent variable list –появится на вашем экране (рис. 49).
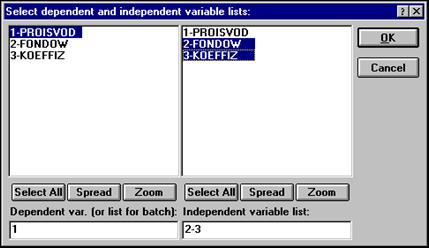 |
Рисунок 49 - Окно выбора переменных для анализа
Высветив имя переменной в левой части окна, выберите зависимую переменную. Высветив имя переменной в правой части окна, выберите независимую переменную. То же можно сделать, просто набрав номера переменных в строках: Список зависимых переменных – Dependent variable listи Список независимых переменных – Independent variable list.
Высветив имена переменных, как показано на рисунке, нажмите кнопку ОКв правом верхнем углу окна Select dependent and independent variable list.Вы вновь окажитесь в стартовой панели модуля. Переменные для анализа выбраны.
Никаких дополнительных установок в стартовой панели в данном случае не нужно.
Нажмите кнопку ОКв правом углустартовой панели.
Шаг 3.На экране перед вами появится диалоговое окно Построение модели – Model Definition(рис. 50).
 |
Рисунок 50 - Окно построения модели в модуле Множественная регрессия
В данном окне выберите стандартный метод оценивания, в опции Method (Метод): Стандартный (Standard).Далее нажмите кнопку ОК.
Программа произведет оценивание параметров модели стандартным методом, и через секунду на экране появится следующее диалоговое окно результатов.
Шаг 4.В диалоговом окне Результаты Множественной регрессии – Multiple Regression Resultsпросмотрите результаты оценивания. Результаты можно просмотреть в численном и графическом виде.
Окно результатов анализа имеет следующую структуру: верх окна – информационный. Он состоит из двух частей: в первой части содержится основная информация о результатах оценивания, во второй высвечивается значимые регрессионные коэффициенты. Внизу окна Результаты множественной регрессиинаходятся функциональные кнопки, позволяющие просмотреть результаты анализа (рис. 51)
 |
Рисунок 51 - Окно оценивания параметров в примере с продажей акций
Рассмотрим вначале информационную часть окна. В ней содержатся краткие сведения о результатах анализа. А именно:
· Dep. Var. (Имя зависимой переменной).В данном случае – ИРКУТ2.
· No. of Cases (Число наблюдений, по которым построена регрессия).
· Multiple R (Коэффициент множественной корреляции).
· R-square – RI (Квадрат коэффициента множественной корреляции), обычно называемый коэффициент детерминации.
· Adjusted R-square: adjusted RI (Скорректированный коэффициент детерминации), определяемый как:
Adjusted R-square = 1-(1-R-square)*(n/(n-p)),
где n – число наблюдений в модели, p – число параметров модели (число независимых переменных плюс 1, так как в модель включен свободный член).
· Std. Error of estimate (Стандартная ошибка оценки).Эта статистика является мерой рассеяния наблюдаемых значений относительно регрессионной прямой.
· Intercept (Оценка свободного члена регрессии).Значение коэффициента А0 в уравнении регрессии.
· Std. Error (Стандартная ошибка оценки свободного члена).Стандартная ошибка коэффициента А0 в уравнении регрессии.
· t (df) and p-value (Значение t-критерия и уровень p). Т- критерий используется для проверки гипотезы о равенстве 0 свободного члена регрессии.
· F– значения F – критерия.
· df– число степеней свободы F – критерия.
· р– уровень значимости.
Шаг 5.Перейдем в функциональную часть окна результатов.
Прежде всего, нажмите кнопку Итоговый результат регрессии – Regression summary.На экране появится электронная таблица вывода – spredsheet, в которой представлены итоговые результаты оценивания регрессионной модели.
 |
Рисунок 52 - Итоговая таблица регрессии
Это стандартная таблица вывода регрессионного анализа. В первом столбце таблицы даны значения коэффициентов beta – стандартизированные коэффициенты регрессионного уравнения,во втором – стандартные ошибки beta,в третьем точечные оценки параметров модели:
Далее, стандартные ошибки для A0, A1, значения статистик t-критерия и т.д.
Шаг 6.Оценка адекватности модели. Важным элементом анализа является оценка адекватности модели.
После того как доказана адекватность модели, полученные результаты можно уверенно использовать для дальнейших действий.
Анализ адекватности основывается на анализе остатков.
Остатки представляют собой разности между наблюдаемыми значениями и модельными, то есть значениями, подсчитанными по модели с оцененными параметрами.
В STATISTICA в модуле Множественная регрессия имеется специальное диалоговое окно, в котором проводится всесторонний анализ остатков.
Нажмите кнопку Анализ остатков – Residual Analysis.
Следующее диалоговое окно Анализ остатков – Residual Analysis появится на экране (рис. 53).
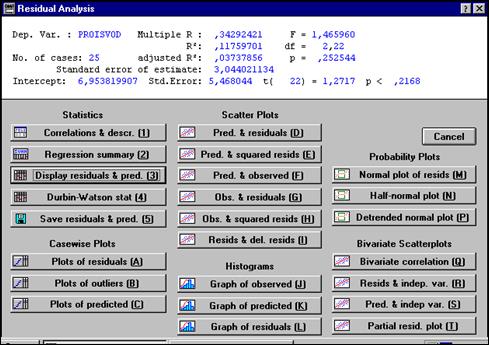 |
Рисунок 53 - Диалоговое окно Анализ остатков в модуле Множественная регрессия
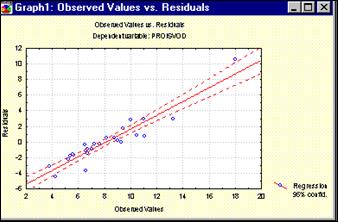 |
Рисунок 54 - График НАБЛЮДАЕМЫЕ ПЕРЕМЕННЫЕ-ОСТАТКИ
Нажмите в этом окне, например, кнопку Obs&residuals. На экране появится график (рис. 54), который говорит о достаточной адекватности модели.
СЛОВАРЬ ТЕРМИНОВ
Причинно-следственные отношения- связь явлений и процессов, когда изменение одного из них - причины - ведет к изменению другого - следствия. Социально-экономические явления - это результат одновременного воздействия большого числа причин.
Признак -основная отличительная черта, особенность изучаемого явления или процесса.
Результативный признак -признак, изменяющийся под действием факторных признаков.
Факторный признак- признак, оказывающий влияние на изменение результативного.
Функциональная связь– связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Стохастическая связь- связь, которая проявляется не в каждом отдельном случае, а в общем, среднем или большом числе наблюдений.
Корреляционная связь- изменение среднего значения результативного признака, которое обусловливается изменением факторных признаков.
Прямая связь- с увеличением или уменьшением значений факторного признака увеличивается или уменьшается значение результативного.
Обратная связь- с увеличением или уменьшением значений факторного признака уменьшается или увеличивается значение результативного.
Линейная связь- статистическая связь между явлениями, выраженная уравнением прямой линии.
Нелинейная связь- статистическая связь между социально-экономическими явлениями, аналитически выраженная уравнением кривой линии (параболы, гиперболы и т.д.).
Корреляция- статистическая зависимость между случайными величинами, которая не имеет строго функционального характера, и при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Регрессионный анализ - аналитическое выражение связи, в котором изменение одной величины - результативного признака - обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения.
Парная регрессия- аналитическое выражение связи двух признаков.
Множественная регрессия- модель связи трех и более признаков.
Коэффициент регрессиипоказывает, насколько в среднем изменяется значение результативного признака при изменении факторного на единицу собственного измерения.
Мультиколлинеарность -наличие тесной зависимости между факторными признаками.
Коэффициент эластичностипоказывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%.
Коэффициент детерминациипоказывает, на сколько процентов вариация результативного признака объясняется вариацией i-го признака (частный) или всех вошедших в модель факторных признаков (множественный).
Линейный коэффициент корреляцииопределяет тесноту и направленность связи между двумя коррелируемыми признаками.
Корреляционное отношениепоказывает связь между двумя признаками.
Множественный коэффициент корреляции отражает связь между результативными и несколькими факторными признаками.
Частный коэффициент корреляции показывает степень тесноты связи
между двумя признаками при фиксированном значении остальных факторных признаков.
Экономическая интерпретация модели- основные выводы и заключения на основе расчета и анализа частных коэффициентов эластичности, частных и множественного коэффициента детерминации, О-коэффициента.
Коэффициент ассоциации и контингенции- определение тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп.
Коэффициент взаимной сопряженности Пирсона - Чупрова -определение тесноты связи двух качественных признаков, каждый из которых состоит более чем из двух групп.
Биссериальный коэффициент корреляции- оценивание связи между качественными альтернативными и количественными варьирующими признаками.
Ранг- порядковый номер значения признака, расположенного в порядке возрастания или убывания величин.
Ранжирование -процедура упорядочения объектов изучения, которая выполняется на основе предпочтения значений признака в порядке возрастания или убывания.
Коэффициенты корреляции Спирмена и Кендалла - определение тесноты связи между двумя количественными или качественными признаками после предварительного ранжирования их по возрастанию или убыванию.
Коэффициент конкордации- определение тесноты связи между произвольным числом ранжированных признаков.
ТЕРМИНЫ ПАКЕТА “STATISTICA”
| Add | Добавить |
| Add Cases | Добавить наблюдения |
| Add Variables | Добавить переменные |
| Advanced Intellegent Problem Solver | Расширенный мастер решения задач |
| Advise | Совет |
| Accept | Принять |
| Action | Действие |
| Activation | Активация |
| Activation Function | Функция активации |
| Add Cases | Добавить наблюдения |
| All Layers | Все слои |
| Append Network | Присоединить сеть |
| Apply | Применить |
| Area Under Curve | Площадь под кривой |
| Assigned Cases | Связанные наблюдения |
| Automatic Network Design | Автоматическое построение сети |
| Automatic Network Designer | Автоматический конструктор сети |
| Automatic update on Exit | Автоматически обновлять при выходе |
| Auxiliary | Дополнительно |
| Back Propagation | Обратное распространение |
| Backwards Stepwise | Пошаговое исключение |
| Baseline Errors | Исходные ошибки |
| Basic | Основной |
| Basic Intellegent Problem Solver | Основной мастер решения задач |
| Best | Лучшая |
| Best Network Retention | Сохранение лучшей сети |
| Candidate Network Types | Типы сетей, среди которых производится поиск (сети-кандидаты) |
| Cases (Train, Verify, Test) | Наблюдения (обучающие, контрольные, тестовые) |
| Case Errors | Ошибки наблюдений |
| City-Block Error | Ошибка "городских кварталов" |
| Class Labeling | Разметка классов |
| Class Labeling of Radial Units | Присвоение меток классов радиальным элементам |
| Classes | Классы |
| Classification | Классификация |
| Classification Output Type | Форма результата классификации |
| Classification Statistics | Статистика классификации |
| Classification Confidence Threshold | Доверительный порог классификации |
| Classification Statistics Datasheet | Таблица статистик классификации |
| Cluster Diagram | Диаграмма кластеров |
| Clustering Networks | Сети для кластеризации |
| Commit Network to Network Set | Поместить сеть в набор сетей |
| Complexity | Сложность |
| Confidence | Доверие |
| Confidence limits | Доверительные границы |
| Conjugate Gradient Descent | Спуск по сопряженным градиентам |
| Convert | Преобразование |
| Create Data Set | Создать набор данных |
| Create Network | Создать сеть |
| Cross Verification | Кросс-проверка |
| Crossover Rate | Скорость скрещивания |
| Current Layer | Текущий слой |
| Data Management | Управление данными |
| Data Set | Набор данных |
| Data Set Datasheer | Таблица данных |
| Data Set Editor | Редактор данных |
| Data Set Shuffle | Перемешать данные |
| Default | По умолчанию |
| Definition | Определение |
| Delimiter | Разделить |
| Delta-Bar-Delta | Дельта-дельта с чертой |
| Details | Подробности |
| Detail Shown | Степень подробности |
| Deviation | Отклонение |
| Dimenionality Reduction | Понижение размерности |
| Direct | Прямой |
| Discard | Отвергнуть |
| Division | Деление |
| Division of Cases | Разбиение наблюдений |
| Duration of Design Process | Длительность поиска |
| Dynamic Link Library | Динамически подключаемая библиотека |
| Edit Case Names | Редактировать имена наблюдений |
| Editing Pre/Post Processing | Редактирование параметров пре/постпроцессирования |
| Enlarge Set | Увеличить набор |
| Entropy | Энтропия |
| Epochs | Эпохи |
| Epsilon | Эпсилон |
| Error | Ошибка |
| Error function | Функция ошибки |
| Error Mean | Среднее ошибки |
| Explicit Deviation Assignment | Явное задание отклонений |
| Exponential distribution | Экспоненциальное распределение |
| Feature Selection | Отбор признаков |
| Hidden | Скрытый |
| Hidden Units | Скрытые элементы |
| Generalized Regression | Обобщенная регрессия |
| Generalized Regression Training | Обучение обобщенной регрессии |
| Generation | Поколение |
| Genetic Algorithm Input Selection | Генетический алгоритм отбора входных данных |
| GRNN | Обобщенно-регрессионные сети |
| Group Sets | Сгруппировать множества |
| Ignore | Не учитывать |
| Inform User First | Сначала сообщать пользователю |
| Initialization Algorithms | Алгоритм инициализации |
| Input Variable | Входная переменная |
| Input Feature Selection | Отбор входных признаков |
| Input/Output Variable | Входная/выходная переменная |
| Input Datasheet | Таблица входных значений |
| Intelligent Problem Solver | Мастер решения задач |
| Intelligent Problem Solver Message | Сообщения мастера решения задач |
| IO Settings | Параметры ввода/вывода |
| Isotropic | Изотропный |
| Isotropic Deviation Assignment | Изотропный выбор отклонений |
| Iterations | Число итераций |
| Jog Weights | Встряхнуть веса |
| Keep Diverse | Сохранять разнообразие |
| K-Means | К-средних |
| K-Means Center Assignment | Выбор центров по К-средним |
| K-Nearest Neighbor Deviation | Отклонение по К ближайшим соседям |
| Kohonen Network | Сеть Кохонена |
| Kohonen Training | Обучение Кохонена |
| Layer | Слой |
| Layers Datasheet | Таблица слоев |
| Layers Shown | Показываемые слои |
| Learned Vector Quantization Training | Квантование обучающего вектора |
| Learning rate | Скорость обучения |
| Levenberg-Marquardt | Левенберга-Маркара |
| Linear | Линейный |
| Linear Network | Линейная сеть |
| Lock | Блокировать |
| Logistic | Логистическая |
| Lookahead | Горизонт |
| Loss Coefficient | Коэффициент потерь |
| Loss Matrix | Матрица потерь |
| Main | Главное |
| Mask | Маска |
| Max/SD | Максимальное/(стандартное отклонение) |
| Mean/SD | Среднее/(стандартное отклонение) |
| Median | Медиана |
| Medium | Средняя (длительность поиска) |
| Merge | Объединить |
| Method | Метод |
| MicroScroll | Микро-прокрутка |
| Min/Mean | Минимум/среднее |
| Minimax | Минимаксное |
| Minimum Improvement | Минимальное улучшение |
| Min Proportion | Минимальная доля |
| Missing Value | Пропущенное значение |
| Momentum | Инерция |
| Move Cases | Переместить наблюдения |
| Multilayer Perceptron (MLP) | Многослойный персептрон |
| Mutation Rate | Скорость мутаций |
| Name | Имя |
| Name and Nominals | Имя и номинальные |
| Nearest Neighbor | Ближайший сосед |
| Neighborhood | Окрестность |
| Network Advisor | Наставник |
| Network (Append) | Сеть (добавить) |
| Network Illustration | Схема сети |
| Network Set | Набор сетей |
| Network Set Editor | Редактор набора сетей |
| Network Set Options | Параметры набора сетей |
| Network to Replace | Заменяемая сеть |
| Network Wizard | Мастер создания сети |
| Network for Classification | Сети для задач классификации |
| Neuro-Genetic Input | Нейрогенетический алгоритм |
| Selection Algorithm | отбора входных данных |
| No Layers | Число слоев |
| Noise | Шум |
| Nominal Variables | Номинальное (категориальные) переменные |
| Nonlinear | Нелинейный |
| Normal Distribution | Нормальное распределение |
| Normalization | Нормировка |
| One-off Input Datasheet | Таблица задания одного входного вектора |
| One-of-N | Один-из-N |
| Open Data Set | Открыть набор данных |
| Open Network | Открыть сеть |
| Optimum Threshold | Оптимальный порог |
| Options | Опции |
| Output Type | Тип выхода |
| Output Variable | Выходная переменная |
| Outputs Datasheet | Таблица выходных значений |
| Outputs Shown | Показатель при выводе |
| Partially or unusually defined text values | Частично или нестандартно заданные текстовые значения |
| Penalty | Штраф |
| Performance | Качество |
| Plot | График |
| PNN | Вероятная нейронная сеть |
| Population | Популяция |
| Popup Class Selector | Контекстный выбор класса |
| Predict | Прогнозировать, предсказывать |
| Prediction | Прогноз |
| Pre/Post Processing | Пре/постпроцессирование |
| Pre/Post Processing Datasheet | Таблица пре/постпроцессирования |
| Pre/Post Processing Editor | Редактор пре/постпроцессирования |
| Pre/Post Processing Editor's Datasheet | Таблица редактора пре/постпроцессирования |
| Principal Components | Главные компоненты |
| Principal Components Analysis | Анализ главных компонент |
| Prior probabilities | априорные вероятности |
| Probabilistic | Вероятность |
| Probabilistic Training | Вероятностное обучение |
| Problem Type | Тип задачи |
| Producing a Reduced Data Set | Формирование уменьшенного набора данных |
| Prune | Удалить |
| Pseudo-Inverse | Псевдообратный |
| PSP-function | Постсинаптическая функция |
| Quick Propagation | Быстрое распространение |
| Radial Basis Function (RBF) | Радиальные базисные функции |
| Radial Sampling | Радиальная выборка |
| Rank | Ранг |
| Range | Диапазон, размах |
| Range selection | Выделение диапазона ячеек |
| Ratio | Отношение |
| Real number fields | Поля для вещественных чисел |
| Real-time update | Пересчитывать по ходу |
| Receiver Operating | Операционная характеристика |
| Characteristic (ROC) Redundancy of variables | Избыточность переменных |
| Regression | Регрессия, зависимость |
| Regression Statistics | Статистики регрессии |
| Regularization | Регуляризация |
| Reinitialize | Переустановить, инициализировать |
| Reject | Отвергнуть |
| Replace | Заменить |
| Replace Oldest | Заменить самую первую |
| Replace Worst | Заменить худшую |
| Response Graph | График отклика |
| Response Surface | Поверхность отклика |
| Restore | Восстановить |
| Retain Best Network | Восстановить лучшую сеть |
| RMS (Root Mean Squared) error | Среднеквадратичная ошибка |
| Run | Запуск |
| Run All Cases | Прогнать все наблюдения |
| Run Data Set | Прогнать набор данных |
| Run One-off Case | Прогнать отдельное наблюдение |
| Run Single Case | Прогнать одно наблюдение |
| Run/Activations | Запуск/активации |
| S.D. (Standard Deviation) Ratio | Отношение стандартных отклонений |
| Sample | Выборка |
| Subsample | Подвыборка |
| Save as Type | Тип сохраняемого файла |
| Scale | Масштаб |
| Select | Выбрать |
| Sensitivity Analysis | Анализ чувствительности |
| Set Case Types | Задать типы наблюдений |
| Set Variable Types | Задать типы переменных |
| Set Weights | Задать веса |
| Shift | Сдвиг, смещение |
| Shuffle | Перемешать |
| Shuffle Cases | Перемешать наблюдения |
| Single Case | Одно наблюдение |
| Single output networks | Сети и одним выходом |
| Smoothing | Сглаживание |
| Smoothing Constant | Константа сглаживания |
| Sort Ascending | Сортировать по возрастанию |
| Sort Descending | Сортировать по убыванию |
| Standart (each case is independent) | Стандартная (наблюдения независимы) |
| Statistics | Статистики |
| Step | Шаг |
| Stopping Conditions | Условия остановки |
| Sum-squared error function | Функция ошибки как сумма квадратов разностей между выходами сети и целевыми значениями |
| Target Error | Целевая ошибка |
| Test | Тестовое (множество) |
| Text Import Wizard | Мастер импорта текста |
| Threshold | Порог |
| Thorough | Полный (режим поиска) |
| Time Series | Временный ряд |
| Time Series Period | Период временного ряда |
| Time Series (predict later values from earlier ones) | Временной ряд (прогноз следующих значений по предыдущим) |
| Time Series Projection | Проекция временного ряда |
| Topological Classes | Топологические классы |
| Topological Map | Топологическая карта |
| Total | Всего |
| Train | Обучить, обучающее множество |
| Train RMS (Root Mean Squared) Error | Среднеквадратичная ошибка обучения |
| Training Error | Ошибка обучения |
| Training Error Graph | График ошибки обучения |
| Training Graph | График обучения |
| Training Set | Обучающее множество |
| Train-Multilayer Perceptrons | Обучение многослойного персептрона |
| Two-State Conversion | Преобразование в два значения |
| Type | Тип |
| Type of Network | Тип сети |
| Unit Length | Единичная длина |
| Unit Names | Имена элементов |
| Unit Penalty | Штраф за элемент |
| Unit Number | Номер элемента |
| Unknown | Неизвестно |
| Unlock | Разблокировать |
| Update | Пересчитать, обновить |
| Value | Значение |
| Variable Definition | Определение переменной |
| Variable type in Data Files | Тип переменных в файлах данных |
| Variant | Вариант |
| Verbose | Подробно |
| Verification Error | Контрольная ошибка |
| Verification Standard Deviation Ratio | Контрольное отношение стандартных отклонений |
| Verification Set | Контрольное множество |
| Verify | Контрольное (множество) |
| Weigend Weight Regularization | Регуляризация весов по Вигенду |
| Weights Distribution | Распределение весов |
| Win Frequencies Datasheet | Таблица частот выигрышей |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1.Ефимова М.Р., Петрова Е.В., Румянцева В.Н. Общая теория статистики: Учебник. – М.: ИНФРА-М, 1998. - С. 339-392.
2.Громыко Г.Л. Общая теория статистики: Практикум. – М.: ИНФРА-М, 1999. – С. 10-14, 109-127.
3.Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – с. 379-432.
4.Ефимова М.Р., Ганченко О.И., Петрова Е.В. Практикум по общей теории статистки: Учеб. пособие. – 2-е изд. перераб. и доп. – М.: Финансы и статистика, 2002. – С. 269-318.
5.Практикум по теории статистики: Учеб. пособие / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 1999. – С. 292-318.
6.Статистика: Учеб. пособие / Под ред. проф. М.Р. Ефимовой. – М.: ИНФРА-М, 2002. – С. 269-308: (серия «Вопрос –ответ»).
7.Бендина Н.В. Экономическая статистика (конспект лекций) – М.: «Издательство ПРИОР», 1999. – С. 58-72.
8.Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник/А.И. Харламов, О.Э. Башина, В.Т. Бабурин и др.; Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 1999. – С. 206-236.
9.Гусаров В.И. Теория статистики: Учебное пособие для вузов. – М.: Аудит, ЮНИТИ, 1998. – С. 159-204.
10. Статистика: Курс лекций/Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. к.э.н. В.Г. Ионина. – Новосибирск: Изд-во НГАЭиУ, М.: ИНФРА-М, 1997. – С. 111-127, 296-307.
11. Башкатов Б.И. Статистика сельского хозяйства с основами общей теории статистки. Курс лекций. – М.: Ассоциация авторов и издателей «ТАНДЕМ». Изд-во «Экмос». – 2001. – С. 79.
12. Ряузов Н.Н. Общая теория статистки: Учебник для студ. экон. спец. вузов. – 3-е изд., перераб. и доп. – М.: Статистика, 1979. – С. 261-291.
13. Кевеш П. Теория индексов и практика экономического анализа: Пер. с венг. М., - 1990.
14. Аллен Р. Экономические индексы: Пер. с англ. М., 1980.
15. Теория статистики: Учебник. Под ред. Р.А. Шмойловой. – М.: Финансы и статистика.
16. Долженкова В.Г. Статистика цен. Учебное пособие. – М.: Информационно-издательский дом «Филинъ». – С. 72-125.
17. Курс социально-экономической статистики. Учебник для вузов / Под. ред. проф. М.Г. Назарова. – М.: Финстатинформ, ЮНИТИ – ДАНА, 2000. – С. 576-673.
18. Практикум по социальной статистике: Учеб. пособие / Под. ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – С. 80-177.
19. Экономическая статистика (Статистика национального богатства (конспект лекций)). – М.: «Издательство ПРИОР», 1999. – С. 81-84.
20. Сборник задач по экономической статистике: Учеб. пособие / Б.Б. Башкатов, Г.М. Гуров, Н.В. Зайцев и др.; - 2-е изд., перераб. и доп. – М.: Финансы и статистика, 1984. – С. 150-162.
21. Практикум по курсу социально-экономической статистики: Учеб. пособие / В.Е. Адамов, И.К. Белявский, А.П. Зинченко и др.; - М.: Финансы и статистика, 1983. – С. 228-276.
ПРИЛОЖЕНИЕ А
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...