
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Повторные независимые испытания
Программные вопросы
2 Повторные независимые испытания. Теорема Бернулли.
3 Теорема Пуассона.
4 Локальная теорема Лапласа.
5 Интегральная теорема Лапласа.
Решение типового примера
Пример 12.4.1.Всхожесть семян данной партии равна 90%. Найти вероятность того, что 1) из пяти посеянных семян взойдёт не менее четырёх; 2) из 100 посеянных семян взойдет 85; 3) из 200 посеянных взойдёт не менее 190. 4) Найдите наивероятнейшее число взошедших семян из 20 посеянных.
Решение. 1) Так как вероятность того, что каждое семя прорастёт р=0,9 и семян для опыта отобрано всего 5, то вероятность того, что прорастет к семян из n посеянных можно найти по формуле Бернулли: Рn(к)=Сnк ркqn-к, где q=1-р.
В нашем случае, вероятность того, что прорастёт не менее четырех семян, находим, используя формулу Бернулли: Р5(к≥4)= Р5(4) + Р5(5)=С54 р4q5-4+ +С55 р5q5-5=  (0,9)4 (1- 0,9) + (0,9)5
(0,9)4 (1- 0,9) + (0,9)5  0,919. Здесь использовано, что Сnк= Сnn-к.
0,919. Здесь использовано, что Сnк= Сnn-к.
2) Так как число посеянных семян достаточно велико, то здесь необходимо использовать локальную теорему Лапласа, в соответствии с которой Рn(к)=  , где
, где  ,
,  .
.
Таким образом, Р100(85)=  =
=  = =
= =  0,1647=0,0549.
0,1647=0,0549.
Значения функции  находят с учётом того, что она чётная по таблице (см. приложение 1).
находят с учётом того, что она чётная по таблице (см. приложение 1).
3) При достаточно большом числе испытаний вероятность того, что событие появится не менее к1 и не более к2 раз в серии из n независимых испытаний, по интегральной теореме Лапласа: Рn (к1  к
к  к2)
к2)  Ф(х2) - Ф(х1), где Ф(х)=
Ф(х2) - Ф(х1), где Ф(х)= 
 . Значения функции Ф(х) находятся по таблице (см. приложение 2) с учётом того, что эта функция нечётная и при х> 4 Ф(х)=0,5.
. Значения функции Ф(х) находятся по таблице (см. приложение 2) с учётом того, что эта функция нечётная и при х> 4 Ф(х)=0,5.
В нашем случае Р200 (190  к
к  200)
200)  Ф(4,71) - Ф(-2,35) = 0,5 +0,4906= =0,9906, так как х1=
Ф(4,71) - Ф(-2,35) = 0,5 +0,4906= =0,9906, так как х1=  , а х2=
, а х2=  .
.
4) Наивероятнейшее число  наступлений события в условиях схемы Бернулли, когда вероятность появления события в каждом испытании одна и та же и равна р, а п – число испытаний, удовлетворяет условию:
наступлений события в условиях схемы Бернулли, когда вероятность появления события в каждом испытании одна и та же и равна р, а п – число испытаний, удовлетворяет условию:
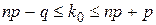 , где
, где 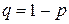 .
.
В нашем случае, р=0,9, q=0,1, п=20, и  , то есть,
, то есть, 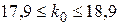 , но
, но  - целое число. Следовательно,
- целое число. Следовательно,  =18.
=18.
Ответ: 1) 0,919; 2) 0,0549; 3) 0,9906; 4) 18.
Пример 12.4.2.Вероятность заболевания животного в стаде равна 0,002. Найдите вероятность того, что среди 1000 голов не окажется больных животных.
Решение. Поскольку вероятность заболевания животного в многочисленном стаде мала, для нахождения требуемой вероятности применим теорему Пуассона, по которой  , где
, где  . В нашем случае п=1000, р=0,0002, k=0 и
. В нашем случае п=1000, р=0,0002, k=0 и  . Для нахождения используем таблицу (см приложение 3):
. Для нахождения используем таблицу (см приложение 3):  0,1353.
0,1353.
Ответ: 0,1353.
Задачи контрольной работы
12.4.1. Доля зараженности зерна вредителями составляет 0,004. Какова вероятность, что в выборке из 1000 зёрен окажется 5 штук зараженных?
12.4.2. Вероятность рождения бычка при отёле коровы равна 0,5. Найти вероятность того, что от 400 коров родится 190 бычков.
12.4.3. Семена некоторой культуры в 1 кг содержат в среднем 3 семени сорняков. Для опытов отвешивается 200г семян. Определить вероятность того, что в них не окажется семян сорняков.
12.4.4. Вероятность неточной сборки прибора равна 0,2. Найти вероятность того, что среди 500 приборов окажется не менее 420 точных.
12.4.5. Вероятность остановки комбайна из-за поломки равна 0,1. Чему равно наивероятнейшее число комбайнов, работающих в поле, если хозяйство имеет 30 комбайнов.
12.4.6. Всхожесть семян груши составляет 70%. Определить вероятность того, что из посаженных четырёх семян взойдут три.
12.4.7. Всхожесть семян пшеницы составляет 85%. Какова вероятность, что из четырех посеянных семян 1) 3 прорастут? 2) не менее трёх прорастёт?
12.7.8. Вероятность поражения земляники серой гнилью равна 0,4. Сколько растений надо взять, чтобы с вероятностью 0,936 можно было утверждать, что выборка содержит хотя бы одно здоровое растение?
12.4.9. Вероятность поражения помидоров фитофторой равна 0,6. Определить вероятность того, что из 100 проверяемых помидоров 55 будет поражено этой болезнью.
12.4.10. Вероятность того, что хотя бы одно из двух семян одной партии взойдёт, равна 0,99. Найти вероятность того, что из пяти семян данной партии взойдет 4.
12.4.11. Нестандартные детали данной партии составляют 8%. Найти вероятность, что из четырёх взятых наугад деталей не менее трёх окажутся стандартными.
12.4.12. На инкубационную закладку поступила партия в количестве 1000 яиц. Вероятность того, что в результате инкубации из яйца вылупится цыплёнок, равна 0,8. Найти наивероятнейшее число вылупившихся цыплят.
12.4.13. Вероятность того, что расход воды в течение дня не превысит норму, равна 0,8. Найти вероятность того, что расход воды будет нормальным в течение 3 из ближайших четырёх дней.
12.4.14. Вероятность поражения яблок паршой равна 0,001. Найти вероятность того, что из 1000 случайно отобранных плодов поражёнными окажутся 2 яблока.
12.4.15. Вероятность изготовления стандартной детали на данном станке равна 0,9. Найти вероятность, что из взятых наугад 300 деталей 250 окажутся стандартными.
12.4.16. Было посажено 400 деревьев. Найти вероятность того, что число прижившихся деревьев составит от 360 до 375, если вероятность приживания отдельного дерева составляет 0,9.
12.4.17. На некотором участке повреждены градом 20% растений. Какова вероятность, что из 100 растений окажутся повреждёнными от 15 до 25 растений?
12.4.18. Птицефабрика поставляет в магазин 90% яиц первой категории. Найти вероятность того, что в партии 10000 яиц число яиц первой категории будет не менее 8900.
12.4.19. Всхожесть семян данной партии равна 90%. Найти вероятность того, что из 100 посеянных взойдёт 95 семян.
12.4.20. Семена пшеницы содержат 0,2% сорняков. Найти вероятность того, что из 1000 семян будет 3 семени сорняков.
Дискретная случайная величина
Программные вопросы
1. Дискретная случайная величина и закон её распределения. Многоугольник распределения.
2. Функция распределения случайной величины.
3. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение; их свойства и вероятностный смысл.
Решение типового примера
Задача 12.5.Для случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета в беспроигрышной лотерее, в которой разыгрывается 100 выигрышей (10 по 50 руб., 30 по 10руб., 60 по 1 руб.), 1) построить ряд распределения; 2) вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение; 3)найти функцию распределения вероятностей.
Решение. 1) Случайная величина в результате испытания принимает одно из своих возможных значений, которое предугадать заранее невозможно. Дискретная случайная величина Х, принимающая значения х1, х2,…, хn с вероятностями р1, р2,…, рn, может быть задана рядом распределения, который записывается в виде таблицы:
| Х | х1 | х2 | … | хn |
| Р | р1 | р2 | … | рn |
В нашем случае возможные значения случайной величины Х: 1, 10 и 50. Вероятности этих значений  ,
,  ,
,  .
.
Получаем ряд распределения:
| Х | |||
| Р | 0,6 | 0,3 | 0,1 |
2) Так как математическое ожидание М(Х) для дискретной случайной величины Х находится по формуле
 ,
,
то получаем: М(Х) = 1∙0,6 +10∙0,3 + 50∙0,1 = 8,6
Дисперсия D(Х) случайной величины Х может быть найдена по формуле:
D(Х) = М(Х2) - [М(Х)]2
Вычислим М(Х2) = 12∙0,6 + 102∙0,3 + 502∙0,1 = 280,6. Тогда D(Х) = 280,6 – (8,6)2 = 206,64.
Среднее квадратическое отклонение  . Получаем:
. Получаем:  .
.
3) Для случайной величины Х функция распределения вероятностей F(x) определяется формулой: F (х) = Р (Х<х)
Для дискретной случайной величины F(x) вычисляется по формуле:
 .
.
Найдём функцию распределения вероятностей.
Если x < 1, то F(x)=Р(Х<х)=Р(-¥ <X< x)=0, так как интервал (-¥; х) не содержит возможных значений Х; если 1< x ≤10, то F(x)=Р(Х<х)= =Р(-¥ <X< x)=P(X=1)=0,6; если 10< x≤50, то F(x)=Р(Х<х)=Р(Х=1)+ Р(Х=10)=0,6+0,3=0,9; если х>50, то F(x)=Р(Х<х)=Р(Х=1)+ Р(Х=10)+Р(Х=50)=0,6+0,3+0,1=1. Итак,
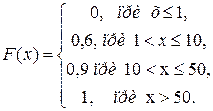
Ответ: 2) М(Х) = 8,6; D(Х) = 206,64. 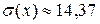 .
.
Задачи контрольной работы
12.5.1. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания или пока не израсходует патроны. Вероятность попадания в цель при каждом выстреле 0,25. Составить закон распределения случайной величины Х – числа израсходованных патронов.
12.5.2. Монета брошена три раза. Случайная величина Х – число появления герба. Написать закон распределения и построить многоугольник распределения случайной величины Х.
12.5.3. Составить закон распределения попадания в цель при четырех выстрелах, если вероятность попадания при одном выстреле 0,25.
12.5.4. Два стрелка делают по одному выстрелу в мишень. Вероятность попадания в нее первым стрелком равна 0,5, вторым – 0,4. Составить закон числа попаданий в мишень.
12.5.5. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент, если в городе четыре библиотеки.
12.5.6. Независимые случайные величины Х и У заданы следующими законами распределения:
| Х | Y | ||||||||
| р | 0,15 | 0,25 | 0,6 | p | 0,1 | 0,35 | 0,15 | 0,4 |
Составить законы случайных величин Х + У, ХУ, 0,5У.
12.5.7. Независимые случайные величины Х и У заданы следующими законами распределения:
| Х | Y | -1 | ||||||||
| р | 0,1 | 0,2 | 0,3 | 0,4 | р | 0,2 | 0,3 | 0,3 | 0,2 |
Составить законы распределения случайных величин Х + У, ХУ.
12.5.8. Дискретная случайная величина Х задана законом распределения:
| Х | ||||
| р | 0,2 | 0,1 | 0,4 | 0,3 |
Найти функцию распределения этой случайной величины и построить ее график.
12.5.9. Дискретная случайная величина Х задана законом распределения:
| Х | |||||
| Р | 0,1 | 0,2 | 0,1 | 0,2 | 0,4 |
Найти функцию распределения этой случайной величины.
12.5.10. Монета брошена три раза. Случайная величина Х – число появления герба. Построить ряд распределения этой случайной величины и найти ее интегральную функцию распределения.
12.5.11. В студенческой группе организована лотерея. Разыгрываются две вещи стоимостью по 15 рублей, и одна стоимостью 55 рублей. Составить закон распределения суммы чистого выигрыша для студента, который приобрел один билет за 2 рубля; всего продано 50 билетов.
12.5.12. Стрелок сделал 3 выстрела по мишени с вероятностью попадания при каждом выстреле 0,6. Найти интегральную функцию распределения числа попаданий по мишени и построить ее график.
12.5.13. Среди 10 лотерейных билетов имеются 4 билета с выигрышем. Наудачу покупают 2 билета. Написать закон распределения вероятностей числа выигрышных билетов среди купленных.
12.5.14. Дискретная случайная величина Х задана законом распределения:
| Х | |||
| р | 0,1 | 0,4 | 0,5 |
Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины Х.
12.5.15. В партии из 20 курток 5 имеют скрытый дефект. Найти закон распределения числа дефектных курток среди 3 купленных.
12.5.16. Дискретная случайная величина Х задана законом распределения:
| Х | -2 | ||
| р | 0,5 | 0,2 | 0,3 |
Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины Х.
12.5.17. Дискретная случайная величина Х задана законом распределения:
| Х | ||||
| р | 0,1 | 0,4 | 0,2 | 0,3 |
Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины Х.
12.5.18. Вероятность выигрыша по одному лотерейному билету 0,4. Приобретено 30 билетов. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение числа билетов, на которые выпадет выигрыш.
12.5.19. Вероятность появления бракованной детали равна 0,3. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение числа годных деталей в партии из 1000 штук.
12.5.20. Проведено 100 независимых испытаний, в каждом из которых вероятность появления некоторого события равна 0,6. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение числа появления события в этих испытаниях.
Непрерывная случайная величина
Программные вопросы
1. Плотность распределения вероятностей для непрерывной случайной величины. Кривая распределения.
2. Числовые характеристики непрерывной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение; их свойства и вероятностный смысл.
Решение типового примера
Задача 12.6.Непрерывная случайная величина Х задана функцией распределения
 .
.
Найти для неё 1) функцию плотности распределения вероятностей f(х); 2) коэффициент а; 2) вероятности попадания в интервалы (1,5; 2) и (0,5; 1,3); 3) математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение. 1) Для непрерывной случайной величины по определению функции плотности вероятностей F’(х)=f(х). Следовательно,
 .
.
2) Так как  , то
, то 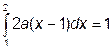 и
и  , следовательно, а=1.
, следовательно, а=1.
3) Вероятность попадания случайной величины Х в заданный интервал находится по формуле: Р(α<Х<β)= F(β) – F(α). Так как а=1, то Р(1,5<X<2)= =F(2)-F(1,5)=(2-1)2 – (1,5-1)2 =1 – 0,52=0,75, а Р(0,5<X<1,3)= F(1,3) – F(0,5) = =(1,3 – 1)2 – 0 = 0,09.
4) Математическое ожидание непрерывной случайной величины Х находится по формуле:
 .
.
Так как вне интервала [1, 2] f(x)=0 и а=1, то М(Х)= = 
 ,
,
Так как дисперсия непрерывной случайной величины находится по формуле  , то в нашем случае
, то в нашем случае 

 .
.
Среднее квадратическое отклонение случайной величины
 =
=  .
.
Ответ: 1) 1; 2) 0,09; 3) М(Х) = 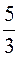 ,
, 


 .
.
Задачи контрольной работы
12.6.1. Случайная величина Х задана функцией распределения
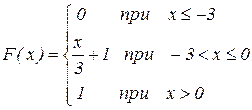
Найти вероятность того, что в результате испытания случайная величина Х примет значение в интервале (-1,0).
12.6.2. Случайная величина Х задана функцией распределения

Определить вероятность того, что случайная величина Х в результате испытания примет значение, больше 0,5, но менее 0,8.
12.6.3. Случайная величина Х задана интегральной функцией распределения:

Определить вероятность того, что случайная величина примет значение в интервале:
а) (1,3; 1,5);
б) (1,2; 1,8).
12.6.4. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.5. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.6. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).
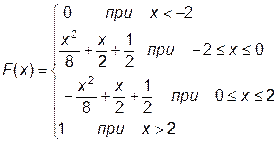
12.6.7. Случайная величина Х задана интегральной функцией распределения F(х). Найти функцию плотности распределения вероятностей f(х).

12.6.8. Непрерывная случайная величина Х задана плотностью распределения:

Найти вероятность того, что Х примет значение в интервале 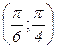 .
.
12.6.9. Непрерывная случайная величина задана плотностью распределения:

Найти вероятность того, что значение случайной величины Х содержится в интервале (1,3).
12.6.10. Плотность распределения вероятностей задана формулой  .
.
Найти коэффициент а и функцию распределения вероятностей случайной величины Х.
12.6.11.Случайная величина Х задана дифференциальной функцией распределения:

Определить коэффициент а.
12.6.12. Случайная величина Х задана плотностью распределения вероятностей f(х). Найти интегральную функцию распределения F(х), если

2.6.13. Случайная величина Х задана плотностью распределения вероятностей f(х). Найти интегральную функцию распределения F(х), если

12.6.14. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):
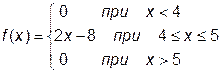
12.6.15. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х), если

12.6.16.Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.17.Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.18. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.19. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):

12.6.20. Вычислить математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х, заданной дифференциальной функцией распределения f(х):
Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...