Необходимые и достаточные условия локального минимума

Определение 1:

- непрерывно-дифференцируема в точке Хо, если существует некоторый вектор - такой что

и

Определение 2:

- непрерывно дифференцированной области VcRⁿ, если - непрерывно дифференцируема для любых

Определение 3:

- дважды непрерывно дифференцируема если существует , такие, что где

G(xo)=f’’(xo) – матрица Гессе 2-х производных

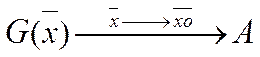
8. Многомерная оптимизация. Основные определения и понятия функции нескольких переменных (ФНП). Обусловленность задачи поиска минимума ФНП.

Рассмотрим функцию n действительных переменных

f(x₁,x₂,...,x_n) = f(x)

Точка в n-мерном евклидовом пространстве с координатами x₁,x₂,x₃,...,x_n обозначается вектором-столбцом x. Градиент функции, т.е. вектор с компонентами

f/ x₁, f/ x₂,..., f/ x_n,

обозначается Ñf (x) или, иногда, g(x). Матрица Гессе (гессиан) функции f(x) обозначается как G(x) и является симметричной матрицей n x n элементов вида

G_ij = ² f/ x_i x_j

Функция f(x) имеет локальный минимум в точке x₀, если существует окрестность точки x₀, такая, что f(x) > f(x₀) во всех точках этой окрестности, т.е. существует положительная величина d, такая, что для |x - x₀| < d справедливо неравенство f(x) >= f(x₀).

В случае глобального минимума в точке x* для всех x справедливо неравенство f(x) >= f(x*).

При таких определениях и очевидных предположениях относительно дифференцируемости можно обобщить уравнение (2.2) из темы №2 и получить:

f(x₀+h)-f(x₀)= h_i (x₁,x₂,..,x_n)+ h_ih_j (x₁,x₂,..,x_n)+... =h + h^TG(x₀)h+... (4)

Тогда, если x₀ является точкой минимума функции f(x), то каждая первая частная производная f/ x_i (i = 1,...,n) должна обращаться в нуль в точке x₀. Если это не так, то соответствующим выбором h_i можно добиться того, что разность f(x₀ + h) - f(x₀ ) будет отрицательна.

Следовательно, необходимым условием минимума в точке x₀ является уравнение

Ñf(x₀)= 0;(5)

т.е.

f(x₀) / x_i = 0, (i=1,...,n), (6)

Тогда знак разности f(x₀ + h) - f(x₀) определяется членом:

1/2 h^TG(x₀)h (7)

Если матрица G(x₀) положительно определена, то этот член положителен для всех h. Следовательно, необходимыми и достаточными условиями минимума являются:

Ñf(x₀) = 0, G(x₀) положительно определена. (8)

Необходимыми и достаточными условиями максимума являются:

Ñf(x_m) = 0, G(x_m) отрицательно определена. (9)

Постановка задачи безусловной оптимизации ФНП. Методы нулевого порядка. Метод покоординатного спуска.

Постановка задачи:

Дана непрерывно дифференцируемая функция F(x1,x2,...,xn) n переменных. Необходимо найти хотя бы одну точку локального оптимума этой функции:

F(x) ---> opt ,где x = (x1,x2,...,xn).

Методы нулевого порядка.

В случае, когда свойства оптимизируемой функции неизвестны или она не является дифференцируемой во всей области поиска, то исследователь вынужден использовать методы нулевого порядка, опирающиеся только на значения функции.

Перед непосредственным применением методов прямого поиска необходимо провести ряд мероприятий по подготовке задачи к решению, а именно

· исключить ограничения в виде равенств;

· определить начальную допустимую точку.

Простейший способ исключения ограничений в виде равенств заключается в решении его относительно одной из переменных с последующим исключением этой переменной путем подстановки полученного выражения в соотношения, описывающие задачу. При этом следует учитывать, что границы значений исключаемых переменных сохраняются в задаче в виде ограничений - неравенств.

Для определения начальной допустимой точки целесообразно использовать процедуру случайного поиска, основная идея которого будет рассмотрена ниже.

После проведения процедуры подготовки задачи к решению следует приметить один из методов условной оптимизации. Рассмотрим методы прямого поиска:

1.2& Метод покоординатного спуска.

Основан на поочередной оптимизации вдоль каждой из координатных осей.

АЛГОРИТМ ПОКООРДИНАТНОГО СПУСКА.

1. Выбор x0 (начального приближения), eps_g и eps_x (точности решения по градиенту и аргументу).

2. iter:= 0; h= 0,1*eps_x. (инициализация счетчика итераций и пробного шага)

3. j=1.

4. x=x0, f0=f(x0)

5. x_j= x0_j+h; Dx=x-x0

6. Расчет значения функции f(x).

7. Если f(x_j)< f0, то p=+Dx, иначе p=-Dx. (направление поиска)

8. Выбор длины шага s=a*p (a>0) вдоль выбранного направления p.

9. x0:= x0 + s; j=j+1;

10. Если j<n, то идти к п.4.

11. iter:=iter+1.

12. Если |s|> eps_x (точность по аргументу), то идти к п.3.

13. Печать вектора x0, значения оптимизируемой функции f(x0) и количества итераций iter.