
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Методы моделирования//необязательная глава
Существует большое количество всевозможных приемов и методов решения функциональных и вычислительных задач. Однако среди имеющегося разнообразия этих методов можно выделить небольшой набор основных, в том смысле, что методы из такого набора применяются часто и лежат в основе многих процедур и алгоритмов. Все обсуждаемые ниже методы рассматриваются на примере решения комбинаторных задач, но сфера их применения, безусловно, намного шире.
Метод частных целей
Этот метод имеет следующую общую формулировку: «Необходимо свести трудную задачу к последовательности более простых задач».
Приведенная рекомендация выглядит столь естественной и разумной, что вряд ли вызовет у кого-нибудь возражения. Более того, любой человек очень часто использует этот метод решения стоящих перед ним задач, при этом, даже не догадываясь (или не отдавая себе отчета) об имеющемся для него (метода) названии. С другой стороны, в конкретной сложной задаче часто очень трудно указать способ ее разбиения на набор более простых задач. Здесь большое значение имеет опыт и искусство специалиста. Тем не менее, несмотря на общность метода и отсутствие «точного рецепта» его применения очень важно освоить этот метод, так как он лежит в основе решения многих задач и по своей сути составляет основу алгоритмизации и программирования. Именно с вопроса «Можно ли данную задачу разбить на последовательность (набор) более простых?» и нужно начинать разработку простого алгоритма.
Неплохой иллюстрацией к применению этого метода является одна из задач сетевого планирования. Подобного рода задачи очень часто приходится решать в системах управления, и их решение является важнейшей функцией АСУ (автоматизированных систем управления).
Пример. Имеется комплекс N=6 взаимосвязанных работ. Для каждой из N работ задана ее трудоемкость в человеко-часах. Необходимо расставить К=10 имеющихся в распоряжении рабочих так, чтобы длительность выполнения всего комплекса работ была минимальной. При этом не разрешается динамически (в ходе выполнения комплекса) перемещать рабочих с одной работы на другую.
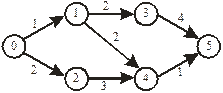 Рисунок 1 – Сетевой график работ
Рисунок 1 – Сетевой график работ
|
Взаимосвязанность работ задается с помощью сетевого графика рис. 1. Он представляет собой ориентированный граф без петель и контуров, состоящий из конечного множества элементов: вершин и попарно соединяющих их дуг.
Вершины графа представляют собой события, а дуги - работы.
Числа над дугами (работами) графа представляют собой трудоемкости работ. Множество полных путей для нашего графика: 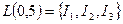 где
где

Общее количество вариантов расстановки рабочих в нашем случае равно  .
.
Одним из самых простых путей решения задачи, который позволяет получить пусть не самое лучшее, но «достаточно хорошее» решение, состоит в следующем. Разбить задачу на 4 шага. На первом шаге решить вопрос, куда поставить 7-го работника, на втором - считая расстановку, полученную на предыдущем шаге, фиксированной (т.е. уже расставленных рабочих полагаем закрепленными за определенными работами), решаем задачу, куда поставить 8-го работника и т.д. Очевидно, что сложную задачу мы разбили на четыре последовательные, более простые задачи. В общем случае количество таких простых задач будет равно  . Каждая из этих однотипных задач может быть сформулирована следующим образом.
. Каждая из этих однотипных задач может быть сформулирована следующим образом.
Необходимо принять решение о добавлении одного работника на одну из работ комплекса так, чтобы время выполнения всего комплекса по получающейся расстановке было минимальным.
В нашей задаче при исходной расстановке шести работников по одному на каждую работу времена на выполнение численно равны трудоемкостям, а длительности полных путей

Продолжительность выполнения всего комплекса работ, таким образом, получается равной 7 часам и определяется продолжительностью самого длинного из полных путей критическому пути I1.
Очевидно, что для того, чтобы снизить длительность выполнения всего комплекса, необходимо поместить имеющегося рабочего на одну из работ этого пути.
Путь I1 состоит из работ (0,1), (1,3) и (3,5). Рассматривая постановку одного рабочего на одну из этих работ и сравнивая получающиеся варианты, выбираем из них вариант с наименьшей продолжительностью выполнения всего комплекса работ в нашем случае это будет постановка рабочего на работу (3,5). Таким образом, задача на добавление одного работника решена, и можно переходить к следующей задаче последовательности.
В общем случае, при поиске решения по данному методу придется проанализировать не более  вариантов.
вариантов.
Метод подъема
Этот метод, как и предыдущий, можно отнести к одному из общих «рецептов» построения модели. Его суть заключается в следующей процедуре. Построение модели начинается с принятия начального предположения или построения начального решения задачи. Затем начинается (насколько возможно) быстрое движение «вверх» от начального уровня по направлению к лучшим решениям. Когда достигается точка, из которой больше невозможно двигаться «наверх», процесс останавливается.
Пример. Имеется предыдущая задача о расстановке рабочих.
Первым шагом является построение начального решения. В нашей задаче о расстановке рабочих начальным решением идет какая-либо расстановка рабочих по работам комплекса. Можно предположить много разных вариантов процедуры начальной расстановки. Рассмотрим одну из простейших. На первом шаге начальной расстановки примем  , для любых i,j ([ ] - означает целую часть числа).
, для любых i,j ([ ] - означает целую часть числа).
На втором шаге оставшееся количество рабочих К mod N распределяется так. Ставится один рабочий на работу с наибольшей трудоемкостью и, если резерв рабочих еще не исчерпан, ищется следующая по трудоемкости работа и проводится постановка очередного рабочего и т.д. Процесс заканчивается, когда резерв рабочих исчерпан. В рассматривавшемся примере расстановка может быть такой:

Как видим, путь I1 оказался критическим путем. Второй элемент алгоритма подъема - процедура восхождения от худшего к лучшему - в нашей задаче может быть определена так. Надо взять одного рабочего с работы, не лежащей на критическом пути, и переместить на одну из работ критического пути. Если результат - длительность выполнения комплекса работ - улучшен, то повторить процесс, если нет, то попробовать переместить рабочего с другой работы и т.д. Если ни одно из возможных перемещений не приводит к улучшению результата, то метод подъема завершает свою работу.
Последнее изменение этой страницы: 2017-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...