
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
8)
Свойства
Локальные
- Функция, непрерывная в точке
 , является ограниченной в некоторой окрестности этой точки.
, является ограниченной в некоторой окрестности этой точки. - Если функция
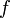 непрерывна в точке
непрерывна в точке  и
и  (или
(или  ), то
), то 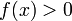 (или
(или  ) для всех
) для всех 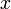 , достаточно близких к
, достаточно близких к  .
. - Если функции
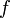 и
и 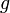 непрерывны в точке
непрерывны в точке  , то функции
, то функции 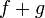 и
и 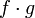 тоже непрерывны в точке
тоже непрерывны в точке  .
. - Если функции
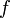 и
и 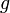 непрерывны в точке
непрерывны в точке  и при этом
и при этом 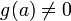 , то функция
, то функция 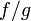 тоже непрерывна в точке
тоже непрерывна в точке  .
. - Если функция
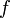 непрерывна в точке
непрерывна в точке  и функция
и функция 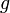 непрерывна в точке
непрерывна в точке 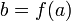 , то их композиция
, то их композиция 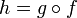 непрерывна в точке
непрерывна в точке  .
.
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции
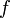 , непрерывной на отрезке
, непрерывной на отрезке  , является отрезок
, является отрезок 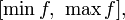 где минимум и максимум берутся по отрезку
где минимум и максимум берутся по отрезку  .
. - Если функция
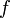 непрерывна на отрезке
непрерывна на отрезке  и
и 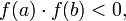 то существует точка
то существует точка  в которой
в которой  .
. - Если функция
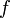 непрерывна на отрезке
непрерывна на отрезке  и число
и число  удовлетворяет неравенству
удовлетворяет неравенству 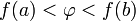 или неравенству
или неравенству  то существует точка
то существует точка  в которой
в которой 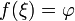 .
. - Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке
 непрерывна в том и только в том случае, когда область ее значений является отрезком с концами
непрерывна в том и только в том случае, когда область ее значений является отрезком с концами 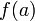 и
и  .
. - Если функции
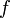 и
и 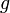 непрерывны на отрезке
непрерывны на отрезке  , причем
, причем  и
и  то существует точка
то существует точка  в которой
в которой  Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
9)
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
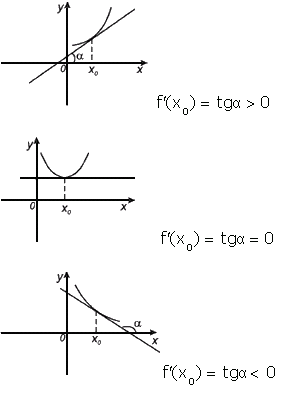
Рассмотрим график функции y = f ( x ):
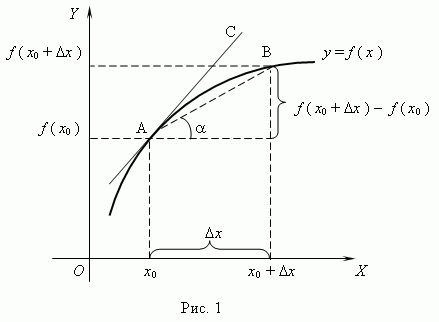
Из рис.1 видно, что для любых двух точек A и B графика функции: 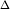 xf(x0+
xf(x0+ 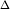 x)−f(x0)=tg
x)−f(x0)=tg  , где
, где  - угол наклона секущей AB.
- угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей.
Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.
10)
Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение D y ее представимо в виде
D y = f'(x)D x +a (D x) D x,
где первое слагаемое линейно относительно D x, а второе является в точке D x = 0 бесконечно малой функцией более высокого порядка, чем D x. Если f'(x)¹ 0, то первое слагаемое представляет собой главную часть приращения D y. Эта главная часть приращения является линейной функцией аргумента D x и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.
Определение 5 (дифференциал).Дифференциалом функции y = f(x) называется главная линейная относительно D x часть приращения D y, равная произведению производной на приращение независимой переменной
dy = f'(x)D x.
Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = D x. Поэтому формулу для дифференциала принято записывать в следующем виде:
| dy = f'(x)dx. | (4) |
Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол f с положительным направлением оси OX, то есть f'(x) = tg f. Из прямоугольного треугольника MKN
KN = MNtgf = D xtg f = f'(x)D x,
то есть dy = KN.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение D x.
Отметим основные свойства дифференциала, которые аналогичны свойствам производной.
- d c = 0;
- d(c u(x)) = c d u(x);
- d(u(x) ± v(x)) = d u(x) ± d v(x);
- d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);
- d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v2(x).
Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме (3) равна y' = f'(u)· u'. Тогда дифференциал функции
dy = f'(x)dx = f'(u)u'dx = f'(u)du,
так как u'dx = du. То есть
| dy = f'(u)du. | (5) |
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
Замечание. Отметим, что в формуле (4) dx = D x, а в формуле (5) du яляется лишь линейной частью приращения функции u.
11)
Теорема Роля (Ролля).
Если функция 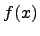 является непрерывной на отрезке [a, b] и дифференцируемой на интервале (a, b), принимает на концах этого интервала одинаковые значения (т.е.
является непрерывной на отрезке [a, b] и дифференцируемой на интервале (a, b), принимает на концах этого интервала одинаковые значения (т.е. 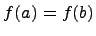 ), то на этом интервале найдётся хотя бы одна точка x=c, в которой производная функции f(x) равна нулю, т.е.
), то на этом интервале найдётся хотя бы одна точка x=c, в которой производная функции f(x) равна нулю, т.е. 
Теорема Ферма Пусть функция  имеет на множестве
имеет на множестве 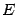 точку экстремума
точку экстремума  , причём множество
, причём множество 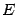 содержит некоторую
содержит некоторую  -окрестность
-окрестность  точки
точки 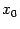 . Тогда либо
. Тогда либо  имеет в точке
имеет в точке 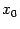 производную, равную 0, то есть
производную, равную 0, то есть  , либо производная в точке
, либо производная в точке 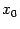 не существует.
не существует.
Теорема Лагранжа Пусть функция  дифференцируема на интервале
дифференцируема на интервале  и непрерывна в точках
и непрерывна в точках  и
и  . Тогда найдётся такая точка
. Тогда найдётся такая точка  , что
, что

|
Теорема Коши Пусть функции  и
и 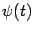 дифференцируемы на интервале
дифференцируемы на интервале  и непрерывны при
и непрерывны при  и
и  , причём
, причём  при всех
при всех  . Тогда в интервале
. Тогда в интервале  найдётся такая точка
найдётся такая точка  , что
, что

12)
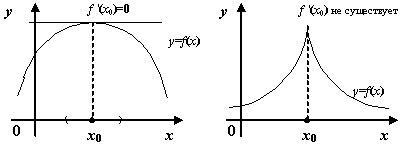
лемма Ферма
Пусть функция  имеет во внутренней точке области определения
имеет во внутренней точке области определения 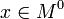 локальный экстремум. Пусть также существуют односторонние производные
локальный экстремум. Пусть также существуют односторонние производные  конечные или бесконечные. Тогда
конечные или бесконечные. Тогда
- если
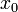 — точка локального максимума, то
— точка локального максимума, то 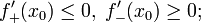
- если
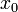 — точка локального минимума, то
— точка локального минимума, то 
В частности, если функция 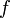 имеет в
имеет в 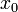 производную, то
производную, то 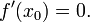
Последнее изменение этой страницы: 2016-06-08
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...