Совет: перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку: а сама-то первообразная найдена правильно?

Определенный интеграл. Примеры решений

Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

В общем виде определенный интеграл записывается так:

Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой a.

Верхний предел интегрирования стандартно обозначается буквой .b

Отрезок называется отрезком интегрирования.

Что такое определенный интеграл? Немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока - определенный интеграл – это ЧИСЛО.

Есть ли у определенного интеграла геометрический смысл? Есть. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?С помощью формулы Ньютона-Лейбница:

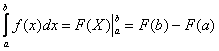
Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию:

3) Подставляем значение нижнего предела в первообразную функцию:

4) Рассчитываем (без ошибок!) разность , то есть, находим число.

Готово.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла 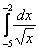не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса.

Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Из вышесказанного следует: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

В упрощенном варианте ситуация выглядит примерно так:

???! Нельзя подставлять отрицательные числа под корень!

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу?Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.

– интеграл вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:

– в таком виде интегрировать значительно удобнее.

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

– это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям:

Пример 1. Вычислить определенный интеграл

Решение:

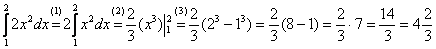
(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы 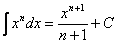. Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2. Вычислить определенный интеграл

Это пример для самостоятельно решения,

Пример 3.Вычислить определенный интеграл

Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: – первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить.

Здесь использованы правила линейности, устно проинтегрировал по таблице. Получилась всего одна скобка с отчёркиванием пределов: (в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, подставлено сначала 4, затем –2, опять же выполнив все действия в уме.

Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, обыкновенные дроби можно считать на калькуляторе. Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту лучше использовать первый способ. Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная находится в одной скобке.

РЕШЕНИЕ ПРИМЕРОВ

Пример 2:Решение:

Пример 4:Решение:

Пример 6:Решение:

Проведем замену переменной:

,Новые переделы интегрирования:

Примечания: В рассмотренном интеграле – как раз тот случай, когда уместно применить свойство определенного интеграла .

Если не совсем понятно, почему из арктангенса можно вынести минус, рекомендую обратиться к методическому материалуГрафики и свойства элементарных функций.

Пример 7:Решение:

Замена:
Новые пределы интегрирования:

Пример 9:Решение:

Интегрируем по частям:

Определенный интеграл. Примеры решений

Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

В общем виде определенный интеграл записывается так:

Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой a.

Верхний предел интегрирования стандартно обозначается буквой .b

Отрезок называется отрезком интегрирования.

Что такое определенный интеграл? Немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока - определенный интеграл – это ЧИСЛО.

Есть ли у определенного интеграла геометрический смысл? Есть. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?С помощью формулы Ньютона-Лейбница:

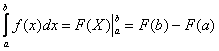
Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию:

3) Подставляем значение нижнего предела в первообразную функцию:

4) Рассчитываем (без ошибок!) разность , то есть, находим число.

Готово.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла 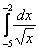не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса.

Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Из вышесказанного следует: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

В упрощенном варианте ситуация выглядит примерно так:

???! Нельзя подставлять отрицательные числа под корень!

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу?Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.

– интеграл вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:

– в таком виде интегрировать значительно удобнее.

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

– это справедливо не только для двух, но и для любого количества функций.

В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.

Для определенного интеграла справедлива формула интегрирования по частям:

Пример 1. Вычислить определенный интеграл

Решение:

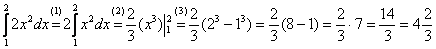
(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы 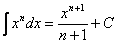. Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Пример 2. Вычислить определенный интеграл

Это пример для самостоятельно решения,

Пример 3.Вычислить определенный интеграл

Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: – первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить.

Здесь использованы правила линейности, устно проинтегрировал по таблице. Получилась всего одна скобка с отчёркиванием пределов: (в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, подставлено сначала 4, затем –2, опять же выполнив все действия в уме.

Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, обыкновенные дроби можно считать на калькуляторе. Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту лучше использовать первый способ. Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная находится в одной скобке.

Совет: перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку: а сама-то первообразная найдена правильно?

Так, применительно к рассматриваемому примеру: перед тем, как в первообразную функцию подставлять верхний и нижний пределы, желательно на черновике проверить, а правильно ли вообще найден неопределенный интеграл? Дифференцируем:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден верно. Теперь можно и формулу Ньютона-Лейбница применить.

Такая проверка будет не лишней при вычислении любого определенного интеграла.

Пример 4. Вычислить определенный интеграл

для самостоятельно решения.