Одноосное напряженное состояние

РАСТЯЖЕНИЕ И СЖАТИЕ

Одноосное напряженное состояние

При растяжении и сжатии в поперечных сечениях бруса (стержня) возникают только нормальные (продольные) силы (N), а все другие внутренние силовые факторы равны нулю. Приложим внешнюю нагрузку P к торцу стержня. Мысленно производим поперечное рассечение образца, при этом площадь сечения равна F. Рассмотрим условие равновесия выделенного участка (рис.2.1). Для однородного стержня внутренние силы распределены по поперечному сечению равномерно, поэтому нормальное напряжение s одинаково во всех его точках. Из условия равновесия внутреннее усилие N равно внешней нагрузке Р.

Уравнение равновесия (рис. 2.1):

-sF + Р = 0, (2.1)

Откуда следует, что напряжение равно:

(2.2)

Правило знаков

Положительное направление нормальных напряжений определяется внешней нормалью к поверхности, ограничивающей рассматриваемую часть тела. Из рассмотрения рис. 2.1 следует, что согласно определению, положительному знаку соответствует растяжение образца, то есть положительное изменение длины (удлинение) а отрицательному – сжатие образца, то есть укорочение.

Несколько внешних сил

При приложении нескольких внешних сил для вычисления напряженного и деформированного состояния необходимо определить внутренние усилия. Характер распределения внутренних сил и их величины не совпадают с картиной внешних сил, поэтому их значения следует определять на основе метода сечений и уравнений равновесия.

Построение эпюр

Для наглядности результаты вычислений представляются в графическом виде путем построения эпюр (графиков функций). Эпюры строятся либо на осевой линии элемента расчетной схемы, либо на вынесенных линиях.

Вычисление и построение эпюр внутренних сил и напряжений целесообразно начинать «от свободного конца». Пусть к стержню, состоящему из 3-х участков (рис.2.2) с площадями сечения F₁, F₂, F₃, в ряде точек приложены нагрузки P₁, P₂, P₃. Между точками приложения нагрузок, на участках a, b, c,d внутренние усилия постоянны. Участок a, очевидно, не нагружен. Из уравнений равновесия последовательно определяем внутренние усилия N₁, N ₂, N₃:

Для сечения на участке b: N₁ + P₁ = 0, откуда N₁ = - P₁

Для сечения на участке c: N₂ + P₂+ P₁ = 0,

откуда: N₂ = -P₂ - P₁

Для сечения на участке d:

N₃ - P₃ + P₂+ P₁ = 0,

откуда: N₃ = P₃ - P₂ - P₁

Первоначально направление неизвестных сил следует принимать в соответствии с положительной ориентацией принятой системы координат, тогда полученный в ходе решения знак минус означает, что в действительности сила имеет противоположное направление. На основе полученных значений N_i строится эпюра внутренних сил (рис.2.3). В зависимости от того, с левого или с правого конца начато вычисление, могут быть получены различные знаки. Поэтому следует сориентировать эпюру так, чтобы сила, соответствующая растяжению откладывалась вверх (по положительному направлению координатной оси).

Последняя из полученных сил соответствует реакции заделки R_A, знак которой показывает, соответствует ли ее направление исходному положительному направлению, учтенному в уравнениях равновесия. На рис.2.3 дополнительно показаны повернутые в направлении построения эпюры векторы внешних и внутренних сил, которые полезны для понимания процесса построения эпюр, но на практике не изображаются. Поделив внутреннее усилие N_i на соответствующее сечение F_i, получим данные для построения эпюры напряжений s_i. Построение эпюры перемещений начинается от заделки, где значение перемещения равно нулю. Для каждого участка определяются деформации Dl_i, которые далее суммируются в направлении от заделки к свободному концу. На концевом участке деформаций нет, но он перемещается как единое целое на величину суммарной деформации, полученной на ранее учтенных участках.

Поперечные деформации

Удлинение стержня в продольном направлении на величину Dl сопровождается его пропорциональным сужением в поперечном направлении на величину Db (рис.2.6).

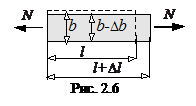Безразмерный коэффициент пропорциональности между относительными деформациями в указанных ортогональных направлениях определяется экспериментально и называется коэффициентом Пуассона m.

e_прод = Dl / l ;

e_попер = Db / b ;

e_попер = m e_{прод .} (2.8)

Коэффициенты ПуассонаТаблица 2.1

Закон Гука для сдвига

При деформации образца изменяются также углы g_a между сечениями (рис.2.7). Из сопоставления линейных и угловых деформаций образца выводится (см.[1]) соотношение для угла сдвига:

g_a = t_a 2(1+m) / E .

Жесткостные свойства материала, характеризующие соотношение его упругости при сопротивлении нормальным и касательным усилиям, связаны соотношением:

G = Е / 2 (1+m) , (2.9)

где G - модуль упругости второго рода, или модуль сдвига. На основании соотношений (2.8) и (2.9) запишем соотношение, именуемое законом Гука для сдвига:

t = g G . (2.10)

Метод сил

В зависимости от того, что принято при решении задач за неизвестные – силы или перемещения, решения носят соответствующие названия: метод сил и метод перемещений. Решение по методу сил имеет меньшую размерность системы уравнений и часто используется при ручном расчете. Однако метод сил сложно формализуется при построении программ для компьютеров и требует высокой квалификации разработчика расчетной схемы. Метод перемещений более универсален, и именно он используется в программах.

Применение метода сил начнем с выбора одной реакции в качестве неизвестной величины. В качестве таковой для рассматриваемого примера выберем реакцию R_а. Если эту реакцию удастся найти, то другую реакцию R_b можно будет определить из уравнения равновесия (а). Неизвестная величина R_а является статически неопределимой, или лишней неизвестной. Если ее отбросить, как показано на рис. 2.11, то получим статически определимую основную систему. Перемещение точки А в основной системе под действиемсилы Р равно:

d_P = Pb / (EF) (b)

и направлено вниз. Далее рассмотрим влияние лишней неизвестной R_a на перемещение точки А (рис.2.12). Вызванное действием этой силы перемещение вверх равно:

d_R = R_a L / (EF) (c)

Полное перемещение d точки А, обусловленное одновременным действием сил Р и R_a, равно сумме d_P и d_R и

согласно условию задачи должно быть равно нулю:

d_P - d_R = 0 (d)

или, учитывая (b), (с) и (d) получим:

Pb / (EF) = R_aL / (EF), (e)

откуда имеем:

R_a = Pb / L (f)

Определив из формулы (f) значение R_a,, из уравнения равновесия (а) можно найти вторую реакцию R_b:

R_b = Pa / L

Метод сил известен также как метод податливостей, поскольку в уравнении совместности перемещений (e) коэффициент L / (EF) при неизвестной величине R_ахарактеризует податливость системы.

Метод перемещений

(Cм. гл. 14.)

Температурные напряжения

Изменение температуры вызывает изменение длины стержня на величину:

d = a L DT , (2.11)

где a – коэффициент линейного температурного расширения. При этом в статически определимой конструкции, которая имеет возможность свободно расширяться и сжиматься, дополнительные напряжения не возникают. В статически неопределимой конструкции изменение температуры вызовет внутренние напряжения. Например, для защемленного стержня, показанного на рис.2.9, и нагруженного только температурой, опорные реакции R должны препятствовать температурному расширению механическими силами, которые вызвали бы равную, но противоположно направленную деформацию:

-d = RL / (EF). (2.12)

Сопоставив выражения (2.11) и (2.12) получим:

R = -EF aDT,

откуда: s = R/F = -a E DT. (2.13)

Знак минус в выражении (2.13) показывает, что при нагревании стержня, концы которого защемлены, он находится в состоянии сжатия.

РАСТЯЖЕНИЕ И СЖАТИЕ

Одноосное напряженное состояние

При растяжении и сжатии в поперечных сечениях бруса (стержня) возникают только нормальные (продольные) силы (N), а все другие внутренние силовые факторы равны нулю. Приложим внешнюю нагрузку P к торцу стержня. Мысленно производим поперечное рассечение образца, при этом площадь сечения равна F. Рассмотрим условие равновесия выделенного участка (рис.2.1). Для однородного стержня внутренние силы распределены по поперечному сечению равномерно, поэтому нормальное напряжение s одинаково во всех его точках. Из условия равновесия внутреннее усилие N равно внешней нагрузке Р.

Уравнение равновесия (рис. 2.1):

-sF + Р = 0, (2.1)

Откуда следует, что напряжение равно:

(2.2)

Правило знаков

Положительное направление нормальных напряжений определяется внешней нормалью к поверхности, ограничивающей рассматриваемую часть тела. Из рассмотрения рис. 2.1 следует, что согласно определению, положительному знаку соответствует растяжение образца, то есть положительное изменение длины (удлинение) а отрицательному – сжатие образца, то есть укорочение.

Несколько внешних сил

При приложении нескольких внешних сил для вычисления напряженного и деформированного состояния необходимо определить внутренние усилия. Характер распределения внутренних сил и их величины не совпадают с картиной внешних сил, поэтому их значения следует определять на основе метода сечений и уравнений равновесия.

Построение эпюр

Для наглядности результаты вычислений представляются в графическом виде путем построения эпюр (графиков функций). Эпюры строятся либо на осевой линии элемента расчетной схемы, либо на вынесенных линиях.

Вычисление и построение эпюр внутренних сил и напряжений целесообразно начинать «от свободного конца». Пусть к стержню, состоящему из 3-х участков (рис.2.2) с площадями сечения F₁, F₂, F₃, в ряде точек приложены нагрузки P₁, P₂, P₃. Между точками приложения нагрузок, на участках a, b, c,d внутренние усилия постоянны. Участок a, очевидно, не нагружен. Из уравнений равновесия последовательно определяем внутренние усилия N₁, N ₂, N₃:

Для сечения на участке b: N₁ + P₁ = 0, откуда N₁ = - P₁

Для сечения на участке c: N₂ + P₂+ P₁ = 0,

откуда: N₂ = -P₂ - P₁

Для сечения на участке d:

N₃ - P₃ + P₂+ P₁ = 0,

откуда: N₃ = P₃ - P₂ - P₁

Первоначально направление неизвестных сил следует принимать в соответствии с положительной ориентацией принятой системы координат, тогда полученный в ходе решения знак минус означает, что в действительности сила имеет противоположное направление. На основе полученных значений N_i строится эпюра внутренних сил (рис.2.3). В зависимости от того, с левого или с правого конца начато вычисление, могут быть получены различные знаки. Поэтому следует сориентировать эпюру так, чтобы сила, соответствующая растяжению откладывалась вверх (по положительному направлению координатной оси).

Последняя из полученных сил соответствует реакции заделки R_A, знак которой показывает, соответствует ли ее направление исходному положительному направлению, учтенному в уравнениях равновесия. На рис.2.3 дополнительно показаны повернутые в направлении построения эпюры векторы внешних и внутренних сил, которые полезны для понимания процесса построения эпюр, но на практике не изображаются. Поделив внутреннее усилие N_i на соответствующее сечение F_i, получим данные для построения эпюры напряжений s_i. Построение эпюры перемещений начинается от заделки, где значение перемещения равно нулю. Для каждого участка определяются деформации Dl_i, которые далее суммируются в направлении от заделки к свободному концу. На концевом участке деформаций нет, но он перемещается как единое целое на величину суммарной деформации, полученной на ранее учтенных участках.