Поток вектора напряжённости электрического поля

Поток вектора напряжённости электрического поля (N) -это скалярная физическая величина, характеризующая распределение электрического поля по поверхности некоторой площади, равная произведению модуля вектора напряженности ( ) на площадь поверхности (S) и на косинус угла ( ) между вектором напряженности ( 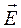) и нормали (перпендикуляра) ( )

однородное электрическое поле с напряжённостью , в котором находится плоская поверхность площадью S

Поток может быть положительным и отрицательным, в зависимости от величины угла a, определяемой направлением нормали к поверхности.

Геометрический смысл потока

Вектора напряжённости

Так как модуль напряжённости определяется числом линий напряжённости, пронизывающих единицу площади поверхности перпендикулярной линиям напряжённости, то поток вектора напряжённости через поверхность площадью S пропорционален числу линий напряжённости, проходящих через данную поверхность.

Поток вектора напряжённости

Через неплоскую поверхность

Вся поверхность разбивается на малые элементы, так, чтобы их можно было считать плоскими, а поле в их пределах – однородным. Затем находят потоки вектора напряжённости через каждый из этих элементов, а полный поток равен алгебраической сумме этих потоков.

,

где N_i – поток вектора напряжённости через один из элементов площади;

k – количество таких элементов.

Поток вектора напряжённости

Через замкнутую поверхность

При определении потока вектора напряжённости через замкнутую поверхность за положительное направление нормали применяется внешняя нормаль (нормаль, направленная наружу области, охватываемой поверхностью).

Если замкнутая поверхность не охватывает заряда, то поток сквозь неё равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий, выходящих из неё.

Теорема Остроградского ─ Гаусса

Для вычисления модуля напряжённости электростатических полей, источником которых являются заряженные тела различной формы, широко используется теорема Остроградского ─ Гаусса.

Поток вектора напряжённости электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, делённой на произведение электрической постоянной и диэлектрической проницаемости среды.

Доказательство

Воспользуемся полем положительного точечного заряда Q. Окружим этот заряд сферой площадью S и радиусом R, центр которой совпадает с точкой нахождения заряда Q.

В каждой точке, лежащей на поверхности этой сферы, модуль напряжённости поля заряда Q будет одинаков и равен

Найдём поток напряжённости через поверхность, данной сферы, для этого разобьём её на малые элементы, найдя потоки вектора напряжённости через каждый элемент. Затем просуммируем алгебраически (с учетом знака) эти потоки.

; ,

так как , то , ;

следовательно, .

Так как , , ; то .

Если заряд находится в непроводящей среде с диэлектрической проницаемостью e, то поток вектора напряжённости электрического поля через замкнутую поверхность, охватывающую этот заряд равен:

Теорема доказана.

Полученный результат будет справедлив для замкнутой поверхности любой формы при любом расположении любого числа зарядов внутри этой поверхности (в этом случае Q – алгебраическая сумма зарядов, находящихся внутри замкнутой поверхности).

Применим теорему Остроградского ─ Гаусса для нахождения модуля вектора напряжённости электростатических полей некоторых заряженных тел.

Модуль вектора напряжённости поля равномерно заряженной сферы (проводящего шара)

Пусть имеется равномерно заряженная сфера радиусаR и с общим зарядом Q. Благодаря равномерному распределению заряда по поверхности сферы поле, созданное ей, обладает сферической симметрией. Поэтому линии напряженности этого поля направлены радиально. Мысленно окружим данную сферу замкнутой поверхностью в виде сферы радиуса r,имеющую общий центр с заряженной сферой.

Рассчитаем модуль вектора напряжённости поля заряженной сферы, используя теорему Остроградского ─ Гаусса.

где

r – расстояние от центра заряженной сферы (шара) до точки, в которой определяется модуль напряжённости поля;

Q – заряд сферы (шара).

При r >R поле убывает с расстоянием по такому же закону, как у точечного заряда. Если r < R,то внутри замкнутой поверхности заряда не будет и тогда, согласно теореме Остроградского ─ Гаусса, внутри равномерно заряженной сферы (проводящего шара) напряженность поля равна нулю , то есть электростатическое поле отсутствует.