
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Искривление пространства: балк и наша брана
В 1912 году Эйнштейн осознал, что если массивные тела способны искривлять время, то должно искривляться и пространство. Но, несмотря на самые напряженные умственные усилия в его жизни, полная картина искривлений пространства долгое время от него ускользала.
Он работал над этим с 1912 года до конца 1915-го. И наконец в ноябре 1915 года благодаря величайшему озарению он вывел свое знаменитое «уравнение гравитационного поля в общей теории относительности», включающее в себя все релятивистские законы, в том числе – искривления пространства.
И снова уровень технологий оказался слабоват для высокоточной проверки[21]. На этот раз потребовалось 60 лет разработок, которые увенчались несколькими решающими экспериментами. Самый, на мой взгляд, интересный из них провели гарвардские ученые Роберт Ризенберг и Ирвин Шапиро. В 1976–1977 годах они передавали радиосигналы двум космическим аппаратам на околомарсианской орбите. Аппараты – они назывались «Викинг-1» и «Викинг-2» – усиливали сигналы и отправляли их обратно на Землю, где замерялось общее время пути сигналов туда и обратно. Поскольку Земля и Марс движутся по орбитам вокруг Солнца, траектории радиосигналов менялись. Сначала они проходили вдалеке от Солнца, затем рядом с Солнцем, затем снова вдалеке (см. рис. 4.3, под графиком).
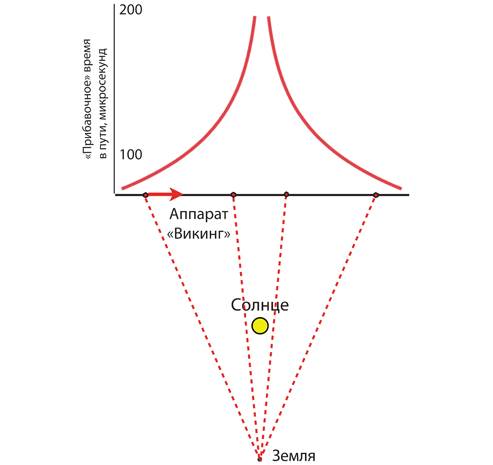
Рис. 4.3. Время пути радиосигналов от Земли до «Викинга» и обратно
Если бы пространство было ровным[22], время пути сигнала менялось бы плавно и монотонно. Но этого не произошло. Когда радиоволны проходили вблизи Солнца, время их пути было больше (на сотни микросекунд) ожидаемого. Это «прибавочное» время показано в верхней части рис. 4.3 как функция от положения «Викинга» – сначала она возрастает, затем убывает. Так вот, один из эйнштейновских законов гласит, что радиоволны и свет всегда распространяются с неизменной скоростью[23]. Следовательно, расстояние от Земли до «Викинга», находящегося вблизи Солнца, должно быть больше ожидаемого – больше на сотни микросекунд, помноженных на скорость света; около 50 километров.
Подобная «добавка к расстоянию» была бы невозможна, будь пространство ровным, как лист бумаги. Следовательно, всему виной искривление пространства вблизи Солнца. Учитывая задержку сигнала и зависимость этой задержки от положения космического аппарата относительно Земли, Ризенберг и Шапиро сделали выводы о форме искривления пространства. Точнее, они рассчитали форму двумерной поверхности, образованной траекториями радиосигналов. Эта поверхность оказалось очень близка к (искривленной) экваториальной плоскости Солнца, поэтому так я и буду ее называть.
Форма найденной учеными поверхности для экваториальной плоскости Солнца показана на рис. 4.4, причем искривление здесь преувеличено. Эта форма в точности совпадает с предсказаниями теории относительности – в пределах погрешности эксперимента, которая составляла 0,001, то есть одну тысячную часть действительного искривления. Вблизи нейтронной звезды искривления пространства гораздо сильнее. А вблизи черной дыры – сильны необычайно.
.

Рис. 4.4. Траектории пути радиосигналов от аппаратов «Викинг» через искривленную экваториальную плоскость Солнца
Экваториальная плоскость Солнца разделяет пространство на две половины – над плоскостью и под ней. Тем не менее на рис. 4.4 экваториальная плоскость изогнута, словно чаша. Внутри Солнца и рядом с ним она прогибается вниз, так что если взять окружность с центром, совпадающим с центром солнечной сферы, то диаметр этой окружности, помноженный на π (3,14159…), окажется больше, чем ее длина, – в случае окружности самого Солнца разница составит примерно 100 километров. Это небольшая разница, но космический аппарат измерил ее с точностью до одной тысячной.
Каким же образом пространство может прогибаться и куда оно может прогибаться? Оно прогибается внутрь многомерного гиперпространства (балка), которое не принадлежит нашей Вселенной!
Об этом стоит рассказать подробнее. На рис. 4.4 экваториальная плоскость Солнца показана как двумерная поверхность, которая прогибается внутрь трехмерного балка. Подобным образом мы, физики, представляем себе Вселенную в целом. У нашей Вселенной три измерения (назовем их «восток – запад», «север – юг» и «верх – низ»), и мы представляем ее себе как трехмерную мембрану (брану), которая прогибается в многомерный балк. Сколько же измерений у балка? Я тщательно разберу этот вопрос в главе 21, но в «Интерстеллар» балк имеет лишь одно дополнительное измерение: итого получается четыре пространственных измерения.
Однако нам с вами очень сложно вообразить, как наша трехмерная Вселенная, наша брана, существует в четырехмерном балке и прогибается в него. Поэтому в этой книге я, изображая нашу брану и балк, опускаю одно измерение, как на рис. 4.4.
Персонажи «Интерстеллар» часто говорят про пять измерений. Три из них – это пространственные измерения нашей браны (восток – запад, север – юг и верх – низ), четвертое – время, а пятое – это дополнительное пространственное измерение балка.
Существует ли балк на самом деле? Есть ли пятое, а возможно, и другие, неизвестные людям измерения? Вполне вероятно, что да. Мы еще рассмотрим этот вопрос в главе 21.
Искривление пространства (нашей браны) играет в «Интерстеллар» важнейшую роль. Например, без него не могло бы существовать червоточины, соединяющей Солнечную систему с далеким участком Вселенной, где находится Гаргантюа. Еще оно искажает звездное небо вокруг червоточины и вокруг черной дыры Гаргантюа; это эффект гравитационного линзирования (см. рис. 3.3).
На рис. 4.5 показан крайний случай искривления пространства. Эту фантастическую иллюстрацию создала моя подруга, художница Лия Хэллоран; на ней изображена гипотетическая область Вселенной со множеством червоточин (см. главу 14) и черных дыр (см. главу 5), которые проникают из нашей браны внутрь балка и сквозь него. Черные дыры сходятся к точкам, которые называются сингулярностями, а червоточины соединяют один участок браны с другим. Здесь, как и раньше, опущено одно измерение браны, из-за чего она выглядит как двумерная поверхность.

Рис. 4.5. Черные дыры и червоточины, проникающие из нашей браны в балк и сквозь него. Одно измерение как браны, так и балка опущено (Рисунок Лии Хэллоран.)
Приливная гравитация
Теория относительности Эйнштейна утверждает, что планеты, звезды и космические аппараты с отключенными двигателями движутся в окрестностях черной дыры по траекториям настолько прямым, насколько это позволяют искривленные дырой пространство и время[24]. На рис. 4.6 дан пример четырех таких траекторий. Две фиолетовые траектории, идущие к черной дыре, сначала были параллельны. Каждая траектория стремилась остаться прямой, и из-за искривления пространства и времени траектории стали сходиться. Зеленые траектории, идущие вокруг дыры, тоже сначала были параллельны. Но из-за искривлений они, наоборот, разошлись в разные стороны.
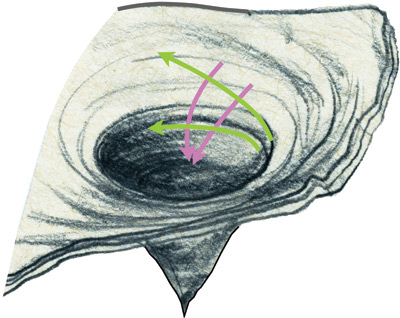
Рис. 4.6. Четыре траектории планетарного движения вблизи черной дыры. Изображение дыры взято с рисунка Лии Хэллоран (рис. 4.5)
Несколько лет назад мы с моими студентами смогли по-новому взглянуть на эти планетарные траектории. В теории относительности Эйнштейна используется такая математическая величина, как тензор Римана. Он подробно описывает искривление пространства и времени. Мы обнаружили заложенные в математическую модель риманова тензора силовые линии, которые одни планетарные траектории сводят вместе, а другие разводят в стороны. Мой студент Дэвид Николс назвал их «тендекс-линиями» (от латинского слова tendere, что значит «растягивать»).
На рис. 4.7 показано несколько тендекс-линий вокруг черной дыры с рис. 4.6. Зеленые траектории начинаются (справа) как параллельные, но затем красные тендекс-линии разводят их в стороны. Я пририсовал фигурку женщины, лежащей на красной тендекс-линии. Она явственно чувствует, как тендекс-линия растягивает ее от макушки до пяток.

Рис. 4.7. Тендекс-линии вокруг черной дыры. Изображение дыры взято с рисунка Лии Хэллоран (рис. 4.5)
Фиолетовые траектории начинаются (сверху) как параллельные, но затем синие тендекс-линии сводят их вместе, и женщина, лежащая на синей тендекс-линии, чувствует сжатие.
Эти растяжения и сжатия – лишь способ описать искривления пространства и времени. С одной стороны, траектории сходятся или расходятся из-за того, что планетарные траектории в искривленном пространстве и времени стремятся к самым прямым путям из возможных. С другой стороны, это происходит из-за растяжений и сжатий, вызванных тендекс-линиями. Следовательно, тендекс-линии должны отображать искривления пространства и времени. Согласно математической модели тензора Римана, так оно и есть.
Черные дыры – не единственные объекты, порождающие силы растяжения и сжатия. Также их вызывают звезды, планеты и их спутники. В 1687 году Исаак Ньютон, работая над своей теорией гравитации, обнаружил эти силы и объяснил с их помощью феномен океанских приливов.
Лунная гравитация сильнее на ближней к Луне стороне Земли, чем на дальней, решил Ньютон. Притяжение «по бокам» Земли направлено слегка «внутрь», поскольку устремлено к центру Луны, и эти направления для каждого из «боков» чуть-чуть различаются. Таков привычный взгляд на лунную гравитацию, схематически изображенный на рис. 4.8 слева.
.

Рис. 4.8. Ньютоновское объяснение океанских приливов на Земле
Усредненная сила гравитационных воздействий остается для Земли как бы незамеченной, поскольку Земля свободно падает вдоль своей орбиты[25]. (Так же как члены экипажа «Эндюранс» не чувствуют притяжения Гаргантюа, пока находятся внутри «Эндюранс», движущегося по орбите вокруг черной дыры. Они испытывают действие лишь центробежных сил, вызванных вращением «Эндюранс» вокруг собственной оси.) А действуют на Землю силы лунного притяжения, обозначенные красными стрелками на левой половине рис. 4.8, за вычетом их усредненной величины – то есть растяжения по направлению к Луне и от Луны и сжатия «с боков» (правая половина рис. 4.8). Это качественно соответствует тому, что происходило бы возле черной дыры.
Эти «ощущаемые» силы оттягивают океанскую воду от земной поверхности на ближней и дальней от Луны сторонах, вызывая приливы. А также притягивают воду к поверхности Земли «с боков», что приводит к отливам. По мере того как Земля поворачивается вокруг своей оси (один полный оборот за 24 часа), мы наблюдаем два прилива и два отлива. Таково, по Ньютону, объяснение океанских приливов, если не считать небольшого осложнения: приливная гравитация Солнца тоже играет роль в этом процессе. Вызываемые ею растяжения и сжатия суммируются с влияниями Луны.
Из-за влияния на приливы и отливы эти гравитационные силы растяжения и сжатия – силы, «ощущаемые» на Земле, – называют приливными. И если рассчитать эти силы по ньютоновским законам тяготения, результат будет с высочайшей точностью соответствовать расчетам по законам теории относительности Эйнштейна. Так и должно быть, поскольку релятивистские законы Эйнштейна и законы Ньютона всегда дают одинаковый результат в условиях умеренной гравитации и значительно меньших, чем скорость света, скоростей.
Согласно релятивистскому объяснению лунных приливов (рис. 4.9), приливные силы возникают из-за синих тендекс-линий, сжимающих Землю «с боков», и красных тендекс-линий, растягивающих в направлении к Луне и от нее. Здесь все так же, как с тендекс-линиями черной дыры (рис. 4.7). Тендекс-линии Луны – это способ зримо представить вызываемые Луной искривления пространства и времени. Поразительно, но столь малое искривление может породить силы столь мощные, что они способны вызывать океанские приливы!
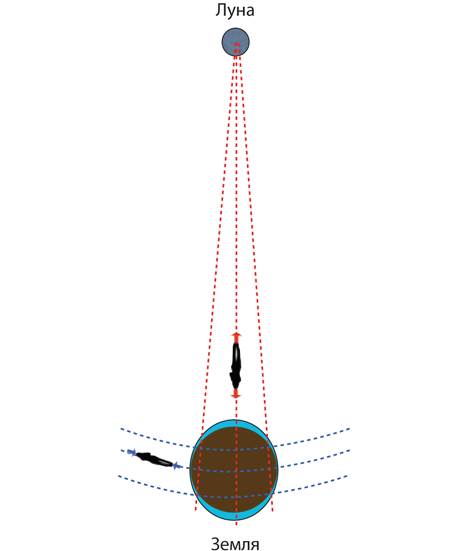
Рис. 4.9. Релятивистское объяснение приливов: тендекс-линии Луны
На планете Миллер (см. главу 17) приливные силы велики невероятно, и это причина возникновения огромных волн, с которыми сталкивается десант во главе с Купером.
Итак, у нас есть три точки зрения на приливные силы:
• Объяснение Ньютона (рис. 4.8): Земля «ощущает» не полное гравитационное притяжение Луны, а полное притяжение (которое различно в разных точках Земли) минус усредненное притяжение.
• Объяснение через тендекс-линии (рис. 4.9): тендекс-линии Луны растягивают и сжимают земные океаны, а тендекс-линии черной дыры (рис. 4.7) растягивают и сжимают траектории планет и звезд вблизи черной дыры.
• Объяснение с помощью наиболее прямого пути (рис. 4.6): траектории движения звезд и планет вокруг черной дыры – самые прямые пути из возможных, учитывая вызванные дырой искривления пространства и времени.
Очень полезно иметь три разные точки зрения на одно явление. Ученые и инженеры львиную долю времени занимаются тем, что решают головоломки, например это может быть задача по проектированию космолета или исследования черной дыры. Как бы то ни было, если одна точка зрения на проблему не дает результатов, может помочь другая. Так профессор Брэнд в «Интерстеллар» подходит к изучению и укрощению гравитационных аномалий (см. главу 24 и главу 25). И таким образом провел бо льшую часть своей взрослой жизни я.
Черные дыры

Черная дыра Гаргантюа играет в «Интерстеллар» ключевую роль. В этой главе мы ознакомимся с общими сведениями о черных дырах, а в следующей – перейдем непосредственно к Гаргантюа. Начну я со странного заявления: черные дыры состоят из искривленного времени и искривленного пространства. И больше ничего – никакой материи. А теперь некоторые пояснения.
Последнее изменение этой страницы: 2016-08-20
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...