Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
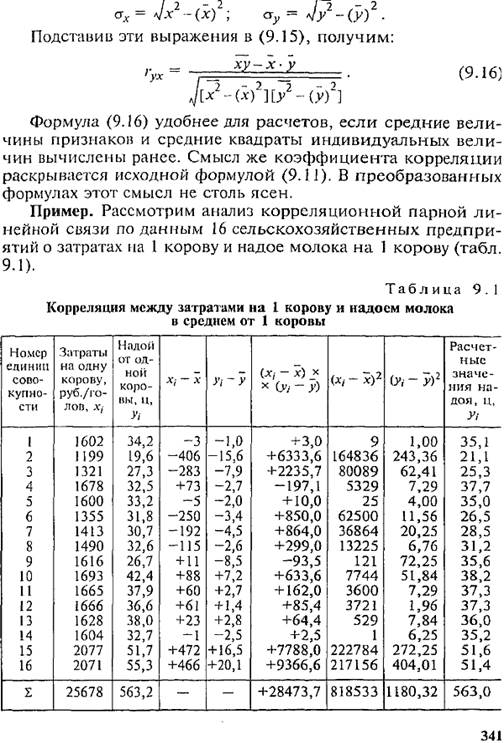
Вычисление и интерпретация параметров парной линейной регрессии
Простейшей системой корреляционной связи является линейная связь между двумя признаками — парная линейная корреляция.
Практическое ее значение в том, что есть системы, в которых среди всех факторов, влияющих на результативный признак, выделяется один важнейший фактор, который в основном определяет вариацию результативного признака. Измерение парных корреляций составляет необходимый этап в изучении сложных, многофакторных связей. Есть и такие системы связей, при изучении которых следует предпочесть парную корреляцию. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связей для выполнения расчетов преобразуются в линейную форму (линеаризуются). Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:
Что касается термина «регрессия», его происхождение таково: создатели корреляционного анализа Ф. Гальтон (1822— 1911) и К. Пирсон (1857—1936) интересовались связью между ростом отцов и их сыновей. Ф. Гальтон изучил более 200 семей и обнаружил, что в группе семей с высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов. Таким образом, отклонение роста от средней в следующем поколении уменьшается — регрессирует. Причина в том, что на рост сыновей влияет не только рост отцов, но и рост матерей и много других факторов развития ребенка, и эти факторы, случайно направленные как в сторону увеличения, так и снижения роста, конечно, приближают рост сыновей к среднему росту. В целом же вариация роста, конечно, не уменьшается, а в наше время «акселерации» сам средний рост увеличивается из поколения в поколение (до известного предела).
Статистическая оценка надежности параметров парной регрессии и корреляции Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не включает в себя величины противоположных знаков. Вероятностная оценка параметров корреляции проводится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. Для коэффициента парной регрессии b средняя ошибка оценки вычисляется как:
мости 0,05) 0,3494, то полученное значение ниже критического по модулю. Соответственно гипотеза о связи признаков надежно не доказана. Неверен будет вывод и об отсутствии связи — он также надежно не доказан. Из табл. П.5 приложения видно, что при малой выборке надежно можно установить только тесные связи, а при большой численности совокупности, например 102 единицы, надежно измеряются и слабые связи. Этот вывод важен для практической работы по корреляционному анализу. Можно рассчитать доверительный интервал оценки коэффициента корреляции с заданной вероятностью, скажем 0,95. При этих условиях и 13 степенях свободы вариации значение /-критерия Стыодента равно 2,16. Тогда доверительный интервал для z составит: 1,564 ± 2,16-0,2774, т.е. от 0,965 до 2,163. Подставив эти граничные значения г в формулу (9.21), получаем границы интервала значений коэффициента корреляции: от 0,747 до 0,974. Как видим, с большой вероятностью связь на самом деле является весьма тесной, коэффициент корреляции не ниже 0,7. |
Последнее изменение этой страницы: 2016-07-28; просмотров: 933
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...