
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА ОТ ДВУХ ЩЕЛЕЙ
ВОЛНОВЫЕ СВОЙСТВА СВЕТА
Методические указания к лабораторным работам
по курсу «Общая физика»
Омск
Издательство ОмГТУ
Составители: Э.М. Ярош, Ю.И. Беликов, О.В. Лях, Т.Н. Кондратьева, О.Ю. Павловская, Е.А. Сидорова, С.С. Ясько.
Данные методические указания разработаны для выполнения лабораторных работ на модульном учебном комплексе МУК–О по разделам общей физики: «Волновая оптика», «Тепловое излучение».
Предназначены для студентов всех специальностей ОмГТУ.
Печатается по решению редакционно-издательского совета
Омского государственного технического университета.
| |
Лабораторная работа № 7-14
ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА ОТ ДВУХ ЩЕЛЕЙ
Цель работы: определение расстояния между щелями с помощью интерференционных полос.
Приборы и принадлежности:модульный лабораторный учебный комплекс МУК – О, миллиметровая линейка, лист белой бумаги.
Краткая теория
Интерференцией света называется явление перераспределения световой энергии в пространстве при сложении (суперпозиции) колебаний от нескольких источников когерентных волн. Рассмотрим два точечных когерентных источника  и
и  , колебания которых происходят с одинаковой частотой, а разность фаз колебаний равна нулю (источники синфазны). Пусть от источника
, колебания которых происходят с одинаковой частотой, а разность фаз колебаний равна нулю (источники синфазны). Пусть от источника  распространяются бегущие волны в среде 1 с показателем преломления
распространяются бегущие волны в среде 1 с показателем преломления 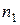 , а от источника
, а от источника  – в среде 2 с показателем преломления
– в среде 2 с показателем преломления  (рис. 1). На рисунке линия
(рис. 1). На рисунке линия  – граница между этими прозрачными средами.
– граница между этими прозрачными средами.
|
 На границе
На границе  выберем точку
выберем точку  и определим условие минимума и максимума амплитуды результирующего колебания в этой точке пространства. Обозначим
и определим условие минимума и максимума амплитуды результирующего колебания в этой точке пространства. Обозначим 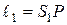 ,
, 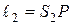 . Для электромагнитных волн (свет – электромагнитная волна) колебания вектора
. Для электромагнитных волн (свет – электромагнитная волна) колебания вектора  от двух одинаковых источников 1 и 2 определяются выражениями:
от двух одинаковых источников 1 и 2 определяются выражениями: 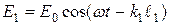 и
и  , где
, где  – амплитуда гармонических колебаний,
– амплитуда гармонических колебаний,  – волновое число,
– волновое число,  – скорость распространения волны.
– скорость распространения волны.
В точке наблюдения  происходит сложение колебаний одинаковой частоты. Будем считать, что эти колебания происходят вдоль одного направления. Разность фаз колебаний в этой точке равна:
происходит сложение колебаний одинаковой частоты. Будем считать, что эти колебания происходят вдоль одного направления. Разность фаз колебаний в этой точке равна:
 ,
,
где 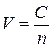 – скорость распространения электромагнитной волны в среде с показателем преломления
– скорость распространения электромагнитной волны в среде с показателем преломления  ;
;  – скорость этой волны в вакууме. Так как
– скорость этой волны в вакууме. Так как
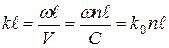 ,
,
где  – волновое число для среды с
– волновое число для среды с  (вакуум),
(вакуум),  – длина волны в среде с
– длина волны в среде с  , то разность фаз колебаний
, то разность фаз колебаний

определяет результирующее колебание в точке  .
.
Величина  – оптический путь волны. Разность этих величин для двух волн
– оптический путь волны. Разность этих величин для двух волн  называют оптической разностью хода волн и
называют оптической разностью хода волн и  . Из условия минимума при сложении колебаний
. Из условия минимума при сложении колебаний  ,
,  (колебания происходят в противофазе) получится
(колебания происходят в противофазе) получится 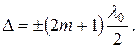 Из условия максимума –
Из условия максимума –  (колебания происходят в одной фазе) определяют условие максимума для
(колебания происходят в одной фазе) определяют условие максимума для 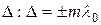 .
.
Можно сказать, что при сложении колебаний в любой точке пространства результирующее колебание определяется величиной оптической разности хода волн.
Методика эксперимента
|
 |
Рассмотрим монохроматическую световую волну (длина волны в вакууме
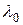 ) с плоским фронтом, падающую на непрозрачный экран с двумя узкими щелями (оптическая схема, близкая к схеме опыта Юнга). Пусть экран, где расположены щели (точечные когерентные источники
) с плоским фронтом, падающую на непрозрачный экран с двумя узкими щелями (оптическая схема, близкая к схеме опыта Юнга). Пусть экран, где расположены щели (точечные когерентные источники  и
и  ), может поворачиваться относительно точки
), может поворачиваться относительно точки 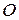 – середины расстояния
– середины расстояния  между источниками
между источниками  и
и  (рис. 2) на некоторый угол
(рис. 2) на некоторый угол  .
.
Экран наблюдения (обычный лист бумаги) располагается на расстоянии  , отсчитываемом от точки
, отсчитываемом от точки 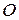 ,
, 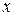 – координата точки наблюдения
– координата точки наблюдения  равна расстоянию
равна расстоянию  .
.
Рассмотрим две световые волны, прошедшие сквозь щели. Оптическая разность хода двух волн от плоского фронта падающей волны до щелей равна  , а оптическая разность хода волн после прохождения щелей равна
, а оптическая разность хода волн после прохождения щелей равна  (
(  ). На экран две волны приходят с разностью хода
). На экран две волны приходят с разностью хода 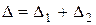 . Рассчитаем
. Рассчитаем  . Из прямоугольных треугольников
. Из прямоугольных треугольников 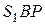 и
и  :
:
 ,
,
 ,
, 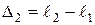 ,
,
 .
.
При условии  :
:  :
:
 ,
,
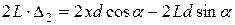 ,
,
или
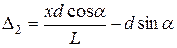 .
.
Тогда
 .
.
Из условия максимума для интерферирующих волн –  , где
, где 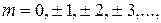 получим
получим  – координаты точек экрана с максимальной интенсивностью света. Расстояние между ними
– координаты точек экрана с максимальной интенсивностью света. Расстояние между ними  . Измеряя
. Измеряя 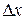 между серединами ярких полос, можно рассчитать расстояние между щелями
между серединами ярких полос, можно рассчитать расстояние между щелями  :
:
 . (1)
. (1)
Порядок выполнения работы
1. По приложению к лабораторным работам (прил. 1) ознакомьтесь с устройством оптического блока.
2. Выведите из рабочей зоны оптические узлы 4, 5, 6, 7 за исключением защитного экрана 3 (прил. 1), плавно поворачивая их в левую сторону до упора.
3. Убедитесь, что кнопки 17 и 25 отжаты.
4. Включите электропитание установки кнопкой 22 «Сеть».
Внимание! Запрещается вставлять и вынимать вилку питания при нажатой кнопке «Сеть», а также включать и выключать кнопку «Сеть» при включенном лазере.
5. Включите лазерный источник света, нажав кнопку 17, при этом должен загореться соответствующий индикатор 14.
Внимание! Категорически запрещается смотреть на прямое лазерное излучение, вносить в рабочую область предметы, способные отражать лазерное излучение (браслеты, зеркала, кольца, …).
6. Вращая турель 2 (прил. 1) установите пиктограмму с двумя щелями под лазерным источником света в положение, перпендикулярное направлению светового потока. При этом риска на втулке  должна указывать на
должна указывать на  .
.
7. Положите чистый лист бумаги на верхнюю крышку электронного блока 11, который будет играть роль экрана.
8. Наблюдайте интерференционную картину в виде чередующихся максимумов и минимумов интенсивности света.
9. Отметьте на бумаге центр нулевого максимума и центры трех или четырех максимумов влево и вправо от нулевого.
10. Измерьте линейкой и запишите в табл. 1 расстояние  между крайними отмеченными максимумами.
между крайними отмеченными максимумами.
11. Рассчитайте среднее расстояние между соседними максимумами интенсивности света по формуле 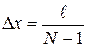 , где
, где  – число отмеченных максимумов.
– число отмеченных максимумов.
12. Повторите пункты 7 – 11 для углов  и
и  , которые устанавливаются поворотом втулки
, которые устанавливаются поворотом втулки  .
.
13. Отключите источник лазерного излучения кнопкой 17 и всю установку кнопкой 22 «Сеть».
14. Рассчитайте по формуле (1) значения величины  (расстояние между щелями) для каждого из выбранных в работе углов
(расстояние между щелями) для каждого из выбранных в работе углов  (значениевеличины
(значениевеличины  указано на панели,
указано на панели, 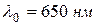 ). Результаты занесите в табл. 1.
). Результаты занесите в табл. 1.
15. Определите среднее значение величины  .
.
16. Рассчитайте абсолютную и относительную погрешности по методу косвенных невоспроизводимых измерений, запишите окончательный результат, сделайте вывод.
Таблица 1
| N п/п | a | 
| N | 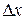
| 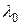
| L | d | <d> | Δd | ε |
| град | мм | мм | мкм | мм | мкм | мкм | мкм | % | ||
Контрольные вопросы
1. Какое явление называется интерференцией световых волн?
2. Какие источники излучения можно считать когерентными?
3. Какое излучение называют монохроматическим?
4. Какова связь оптической и геометрической разностей хода волн?
5. Каким образом разность фаз колебаний связана с оптической разностью хода волн?
6. Условия максимумов и минимумов при интерференции световых волн.
7. Схема установки и порядок выполнения работы.
Лабораторная работа № 7 – 15
ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА
ОТ ОДНОЙ И ОТ ДВУХ ЩЕЛЕЙ
Цель работы: изучение дифракционных картин отодной и от двух щелей в монохроматическом свете от лазерного источника; определение размеров щелей.
Приборы и принадлежности: модульный лабораторный учебный комплекс по оптике (МУК – О), миллиметровая линейка, лист белой бумаги.
Краткая теория
Дифракцией называется огибание световыми волнами препятствий и проникновение света в область геометрической тени.
Различают два случая дифракции. Если источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку наблюдения, образуют практически параллельные пучки, говорят о дифракции Фраунгофера или о дифракции в параллельных пучках. В противном случае говорят о дифракции Френеля или о дифракции в сходящихся пучках.
Большой интерес среди наблюдаемых явлений дифракции представляет собой случай дифракции Фраунгофера от бесконечно длинной щели (для этого достаточно, чтобы длина щели была значительно больше её ширины). На щель шириной  (рис. 1) по нормали падает плоская монохроматическая волна (для лазерного излучения волновой фронт можно считать практически плоским). Параллельный пучок, пройдя сквозь щель, дифрагирует под разными углами в правую и левую сторону от первоначального направления. В результате на экране, расположенном на расстоянии
(рис. 1) по нормали падает плоская монохроматическая волна (для лазерного излучения волновой фронт можно считать практически плоским). Параллельный пучок, пройдя сквозь щель, дифрагирует под разными углами в правую и левую сторону от первоначального направления. В результате на экране, расположенном на расстоянии  от щели, наблюдается дифракционная картина в виде светлой центральной полосы с максимальной освещенностью и симметрично расположенных относительно центральной полосы светлых полос меньшей интенсивности, разделённых темными полосами. Интенсивность дифрагированного света от максимального до минимального значения уменьшается постепенно, как показано на рис. 1. Её распределение по углу дифракции
от щели, наблюдается дифракционная картина в виде светлой центральной полосы с максимальной освещенностью и симметрично расположенных относительно центральной полосы светлых полос меньшей интенсивности, разделённых темными полосами. Интенсивность дифрагированного света от максимального до минимального значения уменьшается постепенно, как показано на рис. 1. Её распределение по углу дифракции 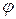 описывается следующей зависимостью:
описывается следующей зависимостью:
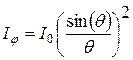 , (1)
, (1)
где  ;
;  – ширина щели;
– ширина щели; 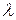 – длина падающей световой волны;
– длина падающей световой волны;  – интенсивность падающего излучения.
– интенсивность падающего излучения.
|
 |
Из этой формулы следует, что максимальная освещённость (максимум света) наблюдается при выполнении условия
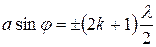 , (2)
, (2)
где  – целое число, определяющее порядковый номер максимума. Самый яркий (центральный) максимум наблюдается при
– целое число, определяющее порядковый номер максимума. Самый яркий (центральный) максимум наблюдается при 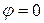 .
.
Освещённость на экране равна нулю (минимум света) при значениях угла дифракции 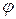 , удовлетворяющих условию
, удовлетворяющих условию
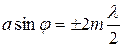 , (3)
, (3)
где  – целое число, определяющее порядковый номер минимума.
– целое число, определяющее порядковый номер минимума.
Направим теперь параллельный пучок монохроматического света на непрозрачную пластинку с двумя щелями шириной  , отстоящими друг от друга на расстоянии
, отстоящими друг от друга на расстоянии  ,
,  (рис. 2). На экране, расположенном на расстоянии
(рис. 2). На экране, расположенном на расстоянии  от пластинки, появится дифракционная картина, являющаяся результатом взаимной интерференции волн, идущих от обеих щелей. Перераспределение интенсивности света, прошедшего через эту систему, можно рассматривать как интерференцию двух дифрагированных лучей. В этом случае интенсивность распределяется по углу дифракции
от пластинки, появится дифракционная картина, являющаяся результатом взаимной интерференции волн, идущих от обеих щелей. Перераспределение интенсивности света, прошедшего через эту систему, можно рассматривать как интерференцию двух дифрагированных лучей. В этом случае интенсивность распределяется по углу дифракции 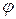 следующим образом:
следующим образом:
 , (4)
, (4)
где  ,
, 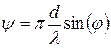 .
.
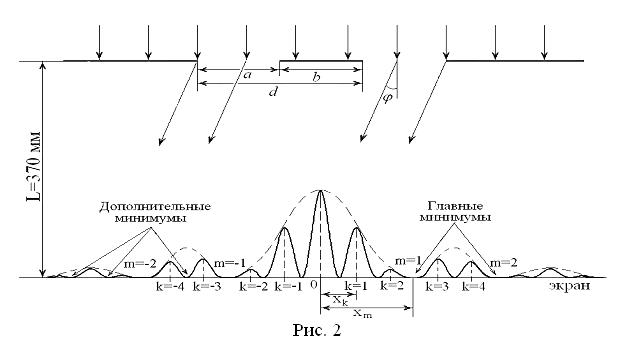 |
Схематичное изображение распределения интенсивности света в дифракционной картине от двух щелей представлено на рис. 2.
|
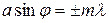 , (5)
, (5)
где  – целое число, определяющее порядковый номер главного минимума. Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Направления, в которых будут наблюдаться дополнительные минимумы, должны удовлетворять следующему условию:
– целое число, определяющее порядковый номер главного минимума. Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Направления, в которых будут наблюдаться дополнительные минимумы, должны удовлетворять следующему условию:
 , (6)
, (6)
где  – целое число, определяющее порядковый номер дополнительного минимума. Наоборот, действие одной щели будет усиливать действие другой, если
– целое число, определяющее порядковый номер дополнительного минимума. Наоборот, действие одной щели будет усиливать действие другой, если
 , (7)
, (7)
где  – целое число, определяющее порядковый номер главного максимума.
– целое число, определяющее порядковый номер главного максимума.
Согласно выражениям (5) и (6), между главными минимумами, например, первого порядка  , содержится не один, а несколько главных максимумов. Между главными минимумами первого порядка расположено
, содержится не один, а несколько главных максимумов. Между главными минимумами первого порядка расположено
 (8)
(8)
светлых интерференционных полос. Огибающая наибольших значений интенсивности света этих нескольких главных максимумов представлена на рис. 2 пунктирной линией.
Порядок выполнения работы
I. Дифракция света на одной щели
1. По приложению к лабораторным работам (прил. 1) ознакомиться с устройством оптического блока.
2. Вывести из рабочей зоны оптические узлы 4, 5, 6, 7, плавно поворачивая их в левую сторону до упора.
3. На верхнюю крышку электронного блока положить лист белой бумаги, который будет играть роль экрана.
4. Убедиться, что кнопки 17, 25 отжаты.
5. Включить электропитание установки кнопкой 22 «Сеть».
Внимание! Запрещается вставлять и вынимать вилку питания при нажатой кнопке «Сеть», а также включать и выключать кнопку «Сеть» при включенном лазере.
6. Включить лазерный источник света, нажав кнопку 17, при этом должен загореться соответствующий индикатор 14.
7. Вращая турель 2 (прил. 1) установить одиночную щель (см. пиктограмму) под лазерным источником в положение, перпендикулярное направлению светового потока. При этом риска на втулке  должна указывать на
должна указывать на  .
.
Внимание! Категорически запрещается смотреть на прямое лазерное излучение, вносить в рабочую зону предметы, способные отражать лазерное излучение (зеркала, кольца, браслеты, …).
8. Зарисовать дифракционную картину, отмечая на бумаге положения центров минимумов интенсивности света, начиная с минимума первого порядка.
9. Измерить линейкой  – расстояние между минимумами
– расстояние между минимумами  и
и 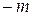 порядков и записать в табл. 1.
порядков и записать в табл. 1.
10. Вращая ручку  , повернуть щель на угол
, повернуть щель на угол 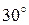 по отношению к первоначальному положению. Пронаблюдать изменение дифракционной картины. Сделать вывод об увиденном.
по отношению к первоначальному положению. Пронаблюдать изменение дифракционной картины. Сделать вывод об увиденном.
11. Вычислить ширину щели  по формуле (3), учитывая, что при малых углах
по формуле (3), учитывая, что при малых углах 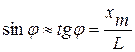 , где
, где  – расстояние от щели до экрана,
– расстояние от щели до экрана,  . Длину волны излучения лазера принять равной
. Длину волны излучения лазера принять равной  .
.
12. Обработать полученные результаты по методу косвенных невоспроизводимых измерений. Вычислить абсолютную и относительную погрешности, записать окончательный результат.
Таблица 1
| m | 
| 
| 
| 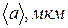
| 
| 
|
II. Дифракция света на двух щелях
1. Установить, повернув турель 2 (прил. 1), на место одиночной щели пластинку с двумя щелями. Убедиться, что плоскость пластинки перпендикулярна лучу, при этом риска на втулке  должна указывать на
должна указывать на 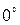 .
.
2. Зарисовать полученную дифракционную картину, отмечая на листе положения главных минимумов (рис. 2) интенсивности света.
3. Измерить линейкой  – расстояние между главными минимумами
– расстояние между главными минимумами  и
и 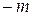 порядков, начиная с
порядков, начиная с 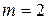 , и записать в табл. 2.
, и записать в табл. 2.
4. Вращая ручку  , повернуть пластину на угол
, повернуть пластину на угол 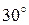 по отношению к первоначальному положению. Пронаблюдать изменение дифракционной картины. Сделать вывод об увиденном.
по отношению к первоначальному положению. Пронаблюдать изменение дифракционной картины. Сделать вывод об увиденном.
5. Выключить лазер кнопкой 17, отключить питание установки кнопкой 22.
6. Вычислить ширину щели  по формуле (3), учитывая, что при малых углах
по формуле (3), учитывая, что при малых углах  , где
, где  – расстояние от щели до экрана,
– расстояние от щели до экрана,  . Длину волны излучения лазера принять равной
. Длину волны излучения лазера принять равной  .
.
7. Вычислить абсолютную и относительную погрешности по методу косвенных невоспроизводимых измерений.
8. Вычислить величину  , подставляя
, подставляя  в формулу (8), учитывая, что между главными минимумами первого порядка находится
в формулу (8), учитывая, что между главными минимумами первого порядка находится 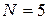 главных максимумов, а затем расстояние между щелями
главных максимумов, а затем расстояние между щелями  . Данные занести в табл. 2.
. Данные занести в табл. 2.
9. Записать окончательный результат.
Таблица 2
| m | 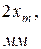
| 
| 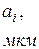
| 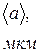
| 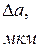
| 
| 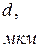
| 
|
Контрольные вопросы
1. Явление дифракции света. Дифракция Френеля и Фраунгофера.
2. Принцип Гюйгенса-Френеля. Объясните с его помощью явление дифракции.
3. Метод зон Френеля.
4. Условия максимумов и минимумов при дифракции света на щели, на двух щелях.
5. Как и почему изменяются положения максимумов и минимумов при повороте объектов исследования по отношению к падающему на них световому пучку?
Лабораторная работа № 7 – 16
ДИФРАКЦИОННЫХ РЕШЕТКАХ
Цель работы: изучение дифракции Фраунгофера на одномерной и двумерной дифракционных решетках в монохроматическом свете.
Приборы и принадлежности: модульный универсальный комплекс МУК – О по оптике, белый лист бумаги, миллиметровая линейка.
Краткая теория
При распространении света в однородной и изотропной среде световые волны не испытывают искажения фронта волны, и свет распространяется прямолинейно.
Явление дифракции заключается в том, что при прохождении через очень узкие отверстия или около краев непрозрачных экранов, свет испытывает отклонение от прямолинейного распространения. При этом наблюдается чередование максимумом и минимумов освещенности (в том числе и в области геометрической тени), т. е. возникает (образуется) интерференционная картина.
Согласно принципа Гюйгенса – Френеля при распространении волн с ограниченным фронтом свет будет наблюдаться только в тех местах, где элементарные волны от всех точек фронта волны складываются в фазе, усиливая друг друга. Наоборот, в тех местах, где элементарные волны, будучи в противофазе, при сложении гасят друг друга, будет наблюдаться темнота (ослабление света).
Если падающие на препятствия лучи образуют параллельные пучки, то говорят о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля или о дифракции в сходящихся пучках.
Одномерная дифракционная решетка представляет собой периодическую систему параллельных щелей одинаковой ширины и расположенных на одинаковом расстоянии друг от друга.
Если  – ширина щели,
– ширина щели,  – расстояние между щелями, то
– расстояние между щелями, то 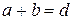 – период (или постоянная) дифракционной решетки.
– период (или постоянная) дифракционной решетки.
Пусть на  щелей одномерной дифракционной решетки нормально падает пучок параллельных лучей. Эти щели можно рассматривать как
щелей одномерной дифракционной решетки нормально падает пучок параллельных лучей. Эти щели можно рассматривать как  когерентных источников света с синфазными колебаниями напряженности электрического поля
когерентных источников света с синфазными колебаниями напряженности электрического поля 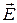 . На каждой щели происходит дифракция света. Дифрагированные под одинаковым углом
. На каждой щели происходит дифракция света. Дифрагированные под одинаковым углом 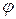 лучи (фраунгоферовский способ наблюдения)
лучи (фраунгоферовский способ наблюдения)  когерентных источников при суперпозиции интерферируют.
когерентных источников при суперпозиции интерферируют.
Поэтому перераспределение интенсивности света, прошедшего через дифракционную решетку, можно рассматривать как интерференцию  -го числа дифрагированных лучей.
-го числа дифрагированных лучей.
В случае дифракции монохроматических лучей с длиной волны 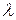 на дифракционной решетке интенсивность света распределяется в зависимости от угла дифракции
на дифракционной решетке интенсивность света распределяется в зависимости от угла дифракции 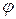 следующим образом:
следующим образом:
 , (1)
, (1)
где  ,
, 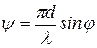 .
.
Для одномерной дифракционной решетки главные максимумы интенсивности света наблюдаются при выполнении условия:
 , (2)
, (2)
где 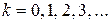 – порядок главного максимума.
– порядок главного максимума.
Самый яркий центральный максимум наблюдается при  . Симметрично относительно него расположены менее интенсивные главные максимумы высших порядков (рис. 1).
. Симметрично относительно него расположены менее интенсивные главные максимумы высших порядков (рис. 1).
При значениях угла дифракции 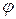 , удовлетворяющих условию
, удовлетворяющих условию
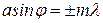 , (3)
, (3)
где  – порядок главного минимума, освещенность на экране равна нулю, т.к. по этим направлениям ни одна из щелей не посылает света.
– порядок главного минимума, освещенность на экране равна нулю, т.к. по этим направлениям ни одна из щелей не посылает света.
При условии (2) векторы напряженности электрического поля всех  лучей от когерентных источников колеблются синфазно и при суперпозиции дают амплитуду результирующего колебания
лучей от когерентных источников колеблются синфазно и при суперпозиции дают амплитуду результирующего колебания
 ,
,
которой соответствует интенсивность света
 , (4)
, (4)
где  – интенсивность света при дифракции на одной щели.
– интенсивность света при дифракции на одной щели.
 |
Между главными минимумами, например, первого порядка (
 ), содержится не один, а несколько главных максимумов, поэтому формула (4) характеризует «огибающую наибольших значений интенсивности света» этих нескольких главных максимумов, показанную на рис. 1 пунктирной линией. Из формулы (4) видно, что дифракционная решетка позволяет резко (в
), содержится не один, а несколько главных максимумов, поэтому формула (4) характеризует «огибающую наибольших значений интенсивности света» этих нескольких главных максимумов, показанную на рис. 1 пунктирной линией. Из формулы (4) видно, что дифракционная решетка позволяет резко (в 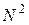 раз) увеличить интенсивность света в области максимумов по сравнению с картиной дифракции на одной щели.
раз) увеличить интенсивность света в области максимумов по сравнению с картиной дифракции на одной щели.
|
 лучей при колебаниях вектора напряженности электрического поля в противофазе. Такие лучи гасят друг друга. Между «дополнительными минимумами» располагаются очень слабые «вторичные максимумы», число которых между соседними главными максимумами равно
лучей при колебаниях вектора напряженности электрического поля в противофазе. Такие лучи гасят друг друга. Между «дополнительными минимумами» располагаются очень слабые «вторичные максимумы», число которых между соседними главными максимумами равно  . На рис. 1 при
. На рис. 1 при  число
число  .
.
Между главными минимумами первого порядка число главных максимумов
 ,
,
а между главными минимумами возрастающих порядков число главных максимумов
 .
.
Ширина главных максимумов зависит от числа  щелей, участвующих в дифракции.
щелей, участвующих в дифракции.
Дифракционная решетка создает эффект резкого разделения максимумов интенсивности света (  (рис. 1)).
(рис. 1)).
При больших расстояниях  (
(  ) от дифракционной решетки до экрана суперпозиция параллельных дифрагированных лучей осуществляется на экране и без собирающей линзы в точке
) от дифракционной решетки до экрана суперпозиция параллельных дифрагированных лучей осуществляется на экране и без собирающей линзы в точке  (рис. 1).
(рис. 1).
Тогда с учетом формул (2) и (3), положение на экране главных максимумов  и минимумов
и минимумов 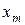 определится соотношениями:
определится соотношениями:
 , (5)
, (5)
где 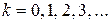
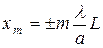 , (6)
, (6)
где 
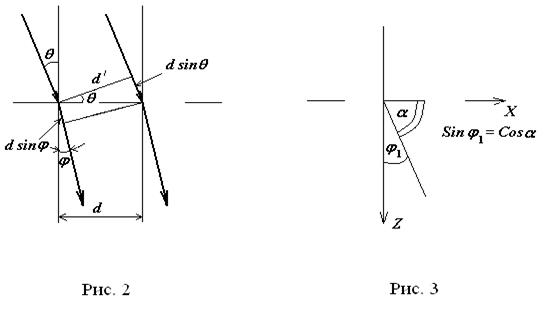
При падении монохроматической волны на прозрачную дифракционную решетку под углом q (рис. 2) оптическая разность хода двух соседних лучей, которые дифрагируют под углом 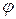 равна:
равна:
 ,
,
|
|
 |
где
 – постоянная дифракционной решетки.
– постоянная дифракционной решетки.
В этом случае, условие (2), при котором наблюдаются главные максимумы интенсивности света, запишется в виде:
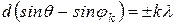 , (7)
, (7)
где 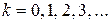 – порядок главного максимума,
– порядок главного максимума, 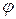 – угол дифракции, определяющий положение
– угол дифракции, определяющий положение 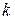 – го максимума.
– го максимума.
Кажущаяся постоянная решетки 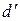 зависит от угла падения
зависит от угла падения  и равна (рис. 2)
и равна (рис. 2)
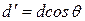 . (8)
. (8)
Следовательно, при большом наклоне 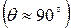 падающего луча кажущаяся постоянная решетки
падающего луча кажущаяся постоянная решетки  становится весьма малой и на решетке с
становится весьма малой и на решетке с  при таком освещении можно наблюдать четкую дифракционную картину.
при таком освещении можно наблюдать четкую дифракционную картину.
Порядок выполнения работы
I. Дифракция света на одномерной дифракционной решетке
1. По приложению к лабораторным работам (прил. 1) ознакомиться с универсальной лабораторной установкой.
2. Вывести из рабочей зоны оптические узлы 4, 5, 6, 7 за исключением защитного экрана 3, плавно поворачивая их в левую сторону до «упора».
3. На верхнюю крышку электронного блока 24 положить лист белой бумаги, который играет роль экрана.
4. Убедиться, что кнопки 25 и 17 электронного блока отжаты.
Внимание!Запрещается вставлять и вынимать вилку питания при нажатой кнопке «Сеть», а также включать и выключать кнопку «Сеть» при включенном лазере.
5. Включить электропитание установки, нажав кнопку 22 «Сеть».
6. Включить лазер, нажав кнопку 17, при этом должен загореться индикатор 14.
Внимание!Категорически запрещается смотреть на прямое лазерное излучение, вносить в рабочую область различные отражающие предметы (браслеты, зеркала, кольца и т. д.).
7. Установить пиктограмму с одномерной дифракционной решеткой, повернув турель 2 вокруг своей оси так, чтобы дифракционная решетка пересекала лазерный луч.
8. Ручку с риской  , которая вращает дифракционную решетку установить на
, которая вращает дифракционную решетку установить на  (дифракционная решетка должна быть перпендикулярна световому лучу лазера, т. е.
(дифракционная решетка должна быть перпендикулярна световому лучу лазера, т. е. 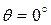 ).
).
9. Карандашом отметить положение центров главных максимумов первых трех порядков (красные полосы) и центрального максимума.
10. Миллиметровой линейкой измерить расстояние 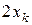 между максимумами
между максимумами 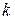 и
и  порядков. Значение
порядков. Значение 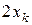 занести в табл. 1.
занести в табл. 1.
11. Вычислить постоянную дифракционной решетки по формуле (5)
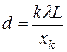 ,
,
где  ,
,  .
.
Значения занести в табл. 1.
12. Найти абсолютную и относительную погрешности вычисления постоянной дифракционной решетки по методу косвенных невоспроизводимых измерений.
13. Повторить пункты 8–12 для угла  , равного
, равного 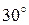 и
и  .
.
14. Вычислить значение величины  по формуле (8):
по формуле (8):
 ,
,
где 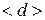 – найденное значение при
– найденное значение при 
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...