Лекція 1 ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК

Лекція 1 ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК

Задачі обчислювальної математики

Розв‘язання задач з використанням методів обчислювальної математики потребує виконання великого обсягу обчислювальних робіт, які можна здійснити за допомогою сучасних ЕОМ. При цьому слід уміти оцінити похибку обчисленого розв‘язку, яка містить:

– похибку математичної моделі (модель описує явище наближено, з припущеннями і спрощеннями);

– неусувну похибку, яка зумовлена похибками у вхідних даних (що отримані, наприклад, за допомогою вимірювань);

– похибки методу (пов‘язані з необхідністю заміни неперервної моделі дискретною або з обривом нескінченного ітераційного процесу після скінченної кількості ітерацій);

– обчислювальні похибки (похибки заокруглення чисел, похибки математичних дій та функцій).

Оцінка похибки може бути здійснена за допомогою:

– абсолютної похибки;

– відносної похибки;

– залишкового члену;

– статистичних оцінок.

Абсолютна і відносна похибки

Наближеним числом а є число, яке незначно відрізняється від точного числа А і замінює його при проведенні обчислень.

Абсолютна похибка наближеного числа а

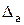= |А - а|. (1.1)

Можливі два випадки:

1) точне число А відоме – тоді абсолютна похибка Δ_а розраховується за формулою (1.1);

2) точне число А невідоме – в такому разі використовують поняття граничної абсолютної похибки

≥ |А - а|. (1.2)

Значення числа А записують так:

А = а ±

Відносна похибка наближеного числа а

δ_а = (1.3)

Часто використовують ще відносну похибку δ_а·100%. Існує також поняття граничної відносної похибки

≥ .

Можна прийняти

= . (1.4)

Оцінка похибки функції (Загальна задача теорії похибок)

Задача полягає у визначенні похибки функції U = f за відомими абсолютними (граничними) похибками аргументів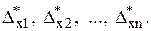

Розв‘язання загальної задачі одержують за допомогою формул:

= ; (1.7)

= = . (1.8)

Приклад 5. Визначити граничні абсолютну і відносну похибки об‘єму кулі при см.

В даній задачі аргументами є і d і π, тому що – теж наближене число. За формулою (1.7) маємо граничну абсолютну похибку

см³.

Гранична відносна похибка

.

Оцінка похибки математичних дій

На підставі формул (1.7), (1,8) можна сформулювати правила оцінки граничних похибок при виконанні математичних дій з наближеними числами.

– Похибки додавання (віднімання)

Нехай , де . Тоді

. (1.9)

Якщо при , то

. (1.10)

– Похибки множення (ділення)

Нехай де . Тоді

(1.11)

Граничну абсолютну похибку легко визначити за формулою

Якщо при , то

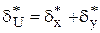. (1.12)

– Похибки ступеня і кореня

Якщо , то . (1.13)

Якщо U = , то . (1.14)

Оцінку похибки будь-якої послідовності математичних дій одержують при послідовному застосуванні наведених вище правил оцінки похибок.

Приклад 6.Визначення граничної відносної похибки функції

виглядає так

Обернена задача теорії похибок

Задача полягає у визначенні абсолютних похибок аргументів функції, при яких абсолютна похибка функції не буде перевищувати заданого значення. Така задача однозначно розв‘язується тільки для функції одного аргументу. У загальному випадку для її розв‘язання використовують припущення про однаковий вклад всіх доданків у формулі (1.7) на формування похибки функції Δ_U, тобто приймають

В такому разі із (1.7) маємо

(1.15)

Приклад 7.Розрахунок абсолютних похибок аргументів функції , якщо (при ) виглядає так

;

Лекція 2. НАБЛИЖЕНІ МЕТОДИ РОЗВ‘ЯЗУВАННЯ НЕЛІНІЙНИХ

(АЛГЕБРИЧНИХ І ТРАНСЦЕНДЕНТНИХ) РІВНЯНЬ

Загальні відомості

Нехай задано рівняння з однією змінною

, (2.1)

де функція 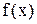визначена і неперервна на деякому проміжку [R_Н, R_В].

Розв‘язати рівняння означає знайти множину його коренів, тобто таких значень [R_Н, R_В], при яких рівняння (2.1) перетвориться в тотожність. Якщо функція 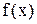– алгебричний багаточлен, то рівняння (2.1) називають алгебричним. Якщо 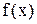містить тригонометричні, показникові або логарифмічні функції, тоді рівняння (2.1) називають трансцендентним.

Універсальних методів для знаходження точних значень коренів алгебричних рівнянь ступеня і трансцендентних рівнянь не існує. Тому важливого значення набувають наближені методи знаходження коренів рівняння з достатньою для практики точністю.

Задача знаходження коренів рівняння (2.1) вважається розв‘язаною, якщо корені обчислені із наперед заданою точністю.

Наближене знаходження коренів рівняння (2.1) складається з двох етапів:

1) відокремлення коренів, тобто виділення проміжків скінченої довжини (відрізків ізоляції коренів) де міститься один єдиний корінь рівняння;

2) обчислення коренів з наперед заданою точністю (уточнення коренів).

Корені рівняння (2.1) можуть бути дійсними і комплексними. Далі розглянуто наближені методи обчислення тільки дійсних коренів.

Відокремлення коренів

Найбільш поширеними методами відокремлення коренів є аналітичний і графічний.

Аналітичний метод передбачає розрахунок значень функції (і її знаків) в ряді точок. Для знаходження відрізків ізоляції коренів рівняння (2.1) в межах зони існування коренів [R_Н, R_В] достатньо визначити точки і , для яких f(a)·f(b) < 0, тобто f(a) і f(b) мають протилежні знаки. Для того, щоб гарантувати, що на відрізку [a, b] є тільки один корінь, необхідно розраховувати значення функції у великій кількості точок, що буває недоцільно.

Графічний метод відокремлення коренів існує в двох різновидах:

1) будують графік функції , знаходять точки перетину графіка з віссю абсцис і визначають навколо цих точок відрізки [a, b];

2) всі члени рівняння (2.1) поділяють на дві групи, одну з яких записують в лівій, а другу – в правій частині рівняння, тобто зображують його у вигляді

і будують графіки функцій і ; далі знаходять межі (відрізки [a, b]), в яких містяться абсциси точок перетину графіків функцій y₁ і y₂.

2.3 До запитання про розв‘язання алгебричних рівнянь

2.3.1 Визначення кількості дійсних коренів

Наближено визначити кількість дійсних додатних коренів алгебричного рівняння

(2.2)

можна за допомогою правила Декарта: кількість дійсних додатних коренів алгебричного рівняння із дійсними коефіцієнтами дорівнює числу змін знаку в послідовності коефіцієнтів рівняння, або на парне число менше (коефіцієнти, що дорівнюють нулю не враховуються).

Кількість від‘ємних коренів алгебричного рівняння дорівнює числу змін знаку в послідовності коефіцієнтів рівняння або на парне число менше.

2.3.2 Визначення області існування коренів

Розглянемо два з декількох методів визначення верхньої межі додатних коренів рівняння .

Метод Лагранжа. Якщо коефіцієнти многочлена відповідають умовам a₀ > 0, a₁, a₂, …,a_m-1 ≥ 0, a_m < 0, то верхня межа додатних коренів рівняння (2.2) визначається за формулою

(2.3)

де В – найбільша із абсолютних величин від‘ємних коефіцієнтів;

m – ступінь х при першому від’ємному коефіцієнті а.

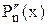Метод Ньютона. Якщо при х = С многочлен і його похідні , … приймають додатні значення, то С є верхньою межею додатних коренів рівняння .

Існує засіб визначення інших меж дійсних коренів з використанням методів визначення верхньої межі додатних коренів .

Якщо

рівняння ,

—″— —″— ,

—″— —″— ,

—″— —″— ,

то всі відмінні від нуля дійсні корені рівняння (якщо вони існують) лежать у середині інтервалів

і .

Визначимо, наприклад, межі додатних і від‘ємних коренів рівняння

.

Знайдемо за методом Лагранжа R₁, R₂, R₃, R₄. У многочлені a₀ = 8

> 0; а₁ = 0; а₂ = -8 < 0; a₃ = -32; a₄ = 1, m = 2. Отже, .

Для многочлена

Аналогічно знаходимо .

Далі, для многочлена

a₀ = 1 > 0; a₁ = -32 < 0, тобто m = 1, B = 32 i R₃ = 1 + 32 = 33.

Зрештою, для многочлена

Маємо a₀ = 1 > 0; a₁ = 32; a₂ = -8; a₃ = 0; a₄ = 8, тобто m = 2; B = 8. Тому .

Отже, якщо задане рівняння має дійсні корені, вони обов‘язково лежать у межах (-2; -1 / 3,828) і (1 / 33; 3).

2.3.3 Обчислення значень многочлена. Схема Горнера

Розв‘язування алгебричних рівнянь як на етапі відокремлення коренів, так і при їх уточненні потребує багаторазових обчислень значень . Тому важливе значення має побудова найбільш економічних (з точки зору кількості операцій) алгоритмів.

Припустимо, що треба розрахувати значення многочлена (див. (2.2)) при . Обчислення вигідно проводити для перетвореного запису (2.2) до наступного вигляду

(2.4)

Послідовне обчислення чисел (n множень і n додавань)

· · · · · · ·

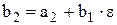
дає значення .

Алгоритм розрахунку , який складено на основі виразу (2.4) називають схемою Горнера. Саме у вигляді схеми розрахунки розташовують так:

ε b₀·ε b₁·ε b₂·ε … b_n-2·ε b_n-1·ε

b₀ b₁ b₂ b₃ … b_n-1 b_n.

В першому рядку записані коефіцієнти многочлена . В третій рядок переносять a₀ = b₀ і далі суму добутку кожного коефіцієнта b_i на ε із а_і+1.

Уточнення коренів

До найбільш поширених методів уточнення коренів алгебричних і трансцендентних рівнянь відносять методи:

– половинного ділення (інші назви: бісекції, дихотомії);

– хорд (помилкового положення);

– дотичних (Ньютона);

2.4.1 Метод половинного ділення

Суть методу, в тому, що відрізок ізоляції кореня [а, b] ділять навпіл точкою х₁ = 0,5(а+b) і обчислюють f(x₁). Якщо f(x₁) = 0, то х₁ є точне значення кореня. Якщо f(x₁) ¹ 0, але (b-a) £ 2ε (ε – задана точність визначення кореня) , то х₁ – є наближене значення кореня що знайдено із заданою точністю. Якщо f(x₁) ¹ 0 і

(b-a) > 2ε, тоді розглядають той з двох відрізків [a, x₁] і [x₁, b], на кінцях якого функція f(x₁) набуває значень протилежних знаків (рис. 2.1). Цей відрізок знов ділять навпіл точкою х₂ (друге наближення кореня) і так само визначають, чи не перевищує абсолютна похибка наближення кореня х₂ величини ε. Очевидно, що знаходження чергового наближення кореня після n ітерацій здійснюється за виразом

x_n+1 = 0,5(a_n + b_n). (2.5)

Рисунок 2.1 – Графічне зображення суті методу половинного ділення

Алгоритм методу половинного ділення можна зобразити таким чином:

Завдання a, b, ε;

R = f(a);

► x = 0,5(a + b);

f(x);

якщо то х – корінь;

да, то ►

інакше R·f(x) < 0 ?

ні, то , R = f(x) ►.

2.4.2Метод хорд

В цьому методі відрізок С ділять не навпіл, а у відношенні f(a) / f(b). Суть методу полягає в тому, що за наближення до кореня приймаються значення x₁, x₂, x₃, …, x_n точок перетину хорди з віссю абсцис (рис. 2.2).

Рисунок 2.2 – Графічне зображення ідеї методу хорд

Наступне наближення кореня визначається за формулою

(2.6)

де с – так звана нерухома точка, за яку приймається той з кінців відрізка [а, b], для котрого знак функції збігається зі знаком другої похідної ( ). На рис. 2.2 с = а. Другий кінець відрізка [а, b] приймається за початкове наближення х₀, що використовується формулою (2.6).

Ітераційний процес закінчується при виконанні умови

,

де – найменше значення модуля першої похідної на відрізку [а, b].

Для використання методу хорд необхідно для інтервалу [a, b] обчислити

і . За допомогою одержаних значень визначити величини m, c, x₀ таким чином: ; якщо f(a) і мають однаковий знак, то с = а і х₀ = b (відповідно, якщо однаковий знак мають f(b) і , то с = b і х₀ = а).

Далі алгоритм методу хорд виглядає так:

Завдання ε, m, c, x₀;

f(c);

R = f(x₀);

► x = ;

f(x);

якщо , то х – корінь;

інакше: R = f(x), x₀ = x ►.

2.4.3 Метод дотичних

Метод полягає в побудові ітераційної послідовності

, (2.7)

що збігається до кореня рівняння f(x) = 0.

Достатні умови збіжності метода: послідовність (2.7) збігається до дійсного значення кореня рівняння f(x) = 0, якщо початкове наближення кореня (х₀) належить інтервалу [а, b], на котрому і зберігають свій знак і задовольняється умова .

За х₀ приймають той з кінців відрізка [а, b], для якого (в методі хорд це нерухома точка).Метод допускає просту геометричну інтерпретацію, а саме: якщо через точку з координатами 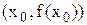провести дотичну, то абсциса точки перетину цієї дотичної з віссю х і є чергове наближення кореня рівняння f(x) = 0 (рис. 2.3).

Ітерації продовжуються до виконання умови

,

Де М – найбільше значення модуля другої похідної на відрізку [а, b],

.

Рисунок 2.3 – Графічне подавання ідеї методу дотичних

Для використання методу дотичних необхідно для інтервалу [a, b] обчислити і . За допомогою одержаних значень визначити величини m, М, x₀ таким чином: ; , якщо f(a) і мають однаковий знак, то х₀ = а.

Далі алгоритм методу дотичних може виглядати так:

Завдання ε, m, М, x₀;

► х = х₀;

f(x);

;

якщо , то х – корінь;

інакше: x₀ = x ►.

Метод дотичних має високу швидкість збіжності, однак недоліком його є необхідність обчислення похідної на кожній ітерації. Якщо мало змінюється на відрізку [а, b], то можна значно зменшити обсяг обчислень, якщо скористуватися модифікованим методом Ньютона з використанням формули

.

2.4.4 Комбінований метод хорд і дотичних

Методи хорд і дотичних дають наближення кореня з різних боків. Тому їх часто поєднують і уточнення кореня відбувається скоріше.

На кожній ітерації використовується спочатку формула (2.7), потім – формула (2.6), в якій за с приймають значення x, що розраховано на даному кроці за формулою(2.7). Процес закінчується, коли Остаточне значення кореня визначається формулою

, (2.8)

де і – наближення кореня, які розраховані відповідно за формулами (2.6) і (2.7).

2.4.5 Метод ітерацій

Для знаходження кореня методом ітерацій (простих) рівняння f(x) = 0 приводять до вигляду так, щоб виконувалось співвідношення , яке є достатньою умовою збіжності ітераційного процесу.

На інтервалі [а, b] обирають початкове наближення х₀ (бажано в середині інтервалу, щоб похибка заокруглення не вивела за межі [а, b], де виконуються умови збіжності); наступні наближення визначаються за формулою

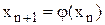(2.9)

доти, поки не буде виконано умову

(2.10)

(можна прийняти ).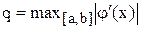

З геометричної точки зору коренем рівняння є абсциса точки перетину кривої і прямої

Характер зміни в процесі обчислень за формулою (2.9), а також вид умови закінчення ітерацій залежать від знака і абсолютної величини на інтервалі [а, b].

– Якщо , то послідовні наближення сходяться до кореня монотонно. При цьому, якщо q £ 0,5 за умову закінчення ітерацій можна прийняти

. (2.11)

– Якщо , то послідовні наближення коливаються навколо дійсного значення кореня і при цьому також можна користуватися умовою (2.11). Таким чином, умову (2.10) необхідно використовувати тільки в тих випадках, коли і .

Не завжди легко обрати функцію , що задовольняє умові збіжності.

Розглянемо один з алгоритмів переходу від рівняння до рівняння Помножимо ліву і праву частини рівняння на довільну константу h і додамо до обох частин невідоме х

при цьому корені вихідного рівняння не зміняться.

Позначимо і одержимо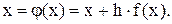

Очевидно, що при будь-яких рівняння і рівносильні. Константу бажано обрати такою, щоб , тоді буде забезпечена збіжність ітераційного процесу.

Похідна . Найбільша швидкість збіжності має місце при , тоді і ітераційна формула (2.9) переходить у формулу Ньютона (метода дотичних)

.

Метод простої ітерації.

В загальному випадку задана СЛАР (3.2), яка записана в розгорнутому матричному вигляді (3.5). Якщо припустити, що діагональні елементи матриці А (і = 1, 2, …, n), то можна перевести систему до канонічного виду і потім виразити х₁ через перше рівняння системи, х₂ – через друге рівняння і т. д. У результаті одержимо систему, яка еквівалентна системі (3.2):

(3.9)

Позначимо 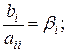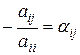, де і, j = 1, 2, …, n. Тоді система (3.9) запишеться так:

(3.10)

Систему (3.10) називають приведеною до нормального виду. Ця система в матричній формі запису:

або

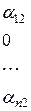
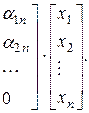(3.11)

Після нормалізації системи перевіряється умова збіжності ітераційного процесу. Ознакою збіжності є умова того, що будь-яка з норм матриці менша від одиниці, тобто

де q – норма матриці , яка може бути визначена за однією із формул:

, .

Алгоритм методу простої ітерації наступний:

- за нульове наближення приймається стовпець вільних членів:

– нульове наближення,

далі будуються матриці-стовпці наступних наближень:

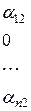
– перше наближення;

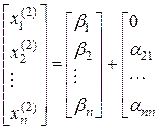
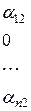
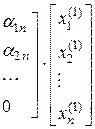– друге наближення

і т.д.

Взагалі, будь-яке (k+1)-е наближення обчислюють за формулою

(k = 0, 1, …, n). (3.12)

Ітераційний процес продовжується доти, поки не буде виконано умову

де – задана абсолютна похибка.

В методі ітерацій заміна значень всіх змінних проводиться одночасно (одночасне зміщення).

Приклад 1. Розрахувати струми в гілках електричного кола (рис. 3.1) методом простої ітерації.

У матричному виді система (1.1) запишеться наступним чином (за даними параметрів схеми рис. 1.1):

або 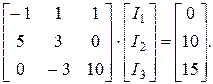(3.13)

Перед приведенням системи до нормального виду необхідно за допомогою еквівалентних перетворювань зробити систему (3.13) придатну ітераційному процесу. Для цього слід за допомогою перестановки і алгебраїчних дій з рівняннями системи добитися, щоб елементи головної діагоналі матриці мали максимальне за модулем значення. Тобто:

- друге рівняння запишеться замість першого;

- з першого рівняння, домноженого на 10 віднімається третє рівняння і результат записується замість другого рівняння;

- третє рівняння залишається без змін.

В результаті система (1.13) набуває виду:

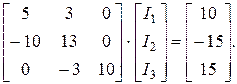(3.14)

Для переводу до нормального виду кожне рівняння системи треба розділити на відповідні елементи, що розташовані на головної діагоналі.

Для СЛАР (3.14), що еквівалентна системі (3.1), нормальний вид наступний:

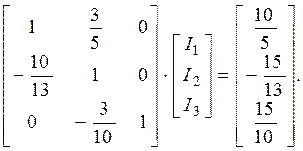(3.15)

Для застосування методу простої ітерації матрична система переписується у формі (3.11), тобто:

.(3.16)

З (3.16) слідує, що 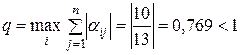і 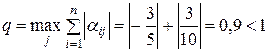, тобто умова збіжності ітераційного процесу (норма матриці менша від одиниці) виконується як по рядках, так і по стовпцях.

Нульове наближення, що дорівнює з (1.12): .

Задається абсолютна похибка розрахунку

Перше наближення згідно ітераційній формулі методу (3.12):

Знаходиться друге наближення:

Третє наближення:

Аналогічно знаходяться наступні наближення розв'язки задачі:

Перевірка умови закінчення ітераційного процесу після 14-го кроку:

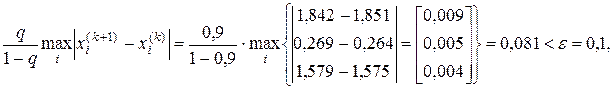
За чотирнадцять кроків ітераційний процес закінчився з заданою точністю.

Струм в гілках схеми (рис. 1.1) становить:

Перевірка у вузлі „а” (рис. 1.1) за першим законом Кірхгофа виконується з точністю до (0,269 + 1,579) – 1,842 = 0,006 А.

Метод Зейделя.

В методі Зейделя уточнене значення х₁ зразу ж використовується для обчислення х₂, далі нові значення х₁ і х₂ використовуються для обчислення х₃ і т. д.

Це невелике удосконалення ітераційної процедури дозволяє суттєво збільшити швидкість збіжності.

Будь-яке (k+1)-е наближення в методі Зейделя будується за наступними формулами:

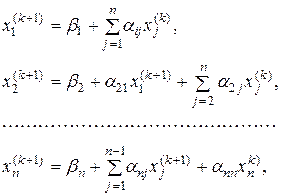(3.17)

де k = 0, 1, 2, …, n.

Ітерації закінчуються, коли із заданою точністю одержано однакові значення невідомих у двох ітераціях підряд.

Умови збіжності ітераційного процесу подібні умовам для простої ітерації, тобто ітераційний процес і його збіжність залежать від величини елементів матриці 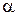наступним чином: якщо найбільша сума модулів елементів рядків або найбільша сума модулів елементів стовпців менше одиниці, то процес ітерації для даної системи збігається до єдиного розв'язку незалежно від вибору початкового наближення.

Отже, умови збіжності можна записати так:

(i = 1, 2, …, n) або (j = 1, 2, …, n).

Як і в методі простої ітерації треба привести СЛАР до виду, який придатний для ітерацій. Для виконання умов збіжності ітераційного процесу достатньо, щоб значення елементів матриці при були невеликими з абсолютної величини. Це рівносильно тому, що якщо для СЛАР модулі діагональних коефіцієнтів кожного рівняння системи більше суми модулів всіх інших коефіцієнтів (без врахування вільних членів), то ітераційні процеси для цієї системи збігаються.

Окремо, на прикладі показується, як виконується еквівалентне перетворення вихідної СЛАР і отримується нормалізована система в загальному випадку.

Вихідна СЛАР:

Виконуються наступні дії:

а) в заданій системі виділяються рівняння з коефіцієнтами, модулі яких більші за суму модулів інших коефіцієнтів рівняння. Кожне виділене рівняння записується в таку строку нової СЛАР, щоб найбільший за модулем коефіцієнт був діагональним. В рівнянні (Q) виконується таке: 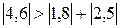. Рівняння (Q) приймається за третє рівняння нової системи.

б) інші рівняння нової еквівалентної системи одержуються шляхом складання лінійних незалежних між собою комбінацій. Так, за перше рівняння можна прийняти таку лінійну комбінацію (P)+(R), тоді:

.

За друге рівняння нової системи – таку комбінацію: (2Q)+(R)-(P), тобто

.

В результаті одержано перетворену СЛАР яка еквівалентна вихідній і задовольняє умовам збіжності ітераційного процесу:

Для перевірки цього твердження еквівалентна система приводиться до нормального виду і перевіряється, чи з