Обратный фотоэффект, фотоионизация и солнечные батареи

Широко используется в практических целях так называемый внутренний фотоэффект, при котором, в отличие от внешнего, оптически возбуждённые электроны остаются внутри освещённого тела, не нарушая нейтральности последнего… Происходит пространственное разделение внутри объёма проводника оптически возбуждённых электронов и микрозон (дырок), возникающих в непосредственной близости от атомов, от которых оторвались электроны… Таким образом достигается прямое преобразование световой энергии в электрическую.

Г.С. Ландсберг, "Оптика" [74]

Последняя разновидность фотоэффекта — обратный фотоэффект: генерация металлом излучения при обстреле его поверхности электронами энергии E (§ 4.1). Электрон при захвате атомом начинает излучать на частоте своего вращения f=E/h (Рис. 156). Подобный же эффект работает и в некоторых светодиодах, где в переходном слое полупроводникового кристалла, края которого находятся под напряжением V, электроны набирают энергию E=eV и, при захвате атомами, закручиваясь в их магнитном поле, излучают на частоте вращения f=eV/h. Ещё раз отметим, что захват и выброс электрона атомом происходит без изменения энергии (без затрат и выделения энергии ионизации), поскольку захват производит магнитное поле нейтрального атома, не меняющее энергии захваченного электрона. Что касается потенциального электрического поля атомного ядра, то оно в принципе не способно захватить электрон. Поэтому, в фотоэффекте электроны лишь малую долю энергии получают от света, основная же часть энергии у них есть изначально. И, не исключено, что однажды опыт покажет: энергия электронов, покинувших металл, порой превосходит энергию выбившего их света. Энергия света идёт лишь на изменение орбиты электрона и отрыв его от атома при сходе с устойчивой орбиты. В фотоэлементах (солнечных батареях) эта энергия освобождения электронов и преобразуется в электрическую. В случае, если бы энергия света шла ещё и на придание скорости электронам, по сути, — на нагрев полупроводника, КПД солнечных батарей было бы существенно меньше известного. Реально же энергия света напрямую, с минимальными потерями, преобразуется в электрическую.

Рис. 156. Прямой (а) и обратный (б) фотоэффекты: выброс электрона атомом под действием света (а) и генерация атомом рентгеновского излучения при захвате электрона.

Вполне возможно, что правильное понимание механизма фотоэффекта позволит ещё сильней повысить КПД солнечных батарей, найти более дешёвые и эффективные полупроводниковые материалы, преобразующие свет в электроэнергию. Пока же поиск таких материалов вёлся вслепую. И, лишь на базе классического подхода, этот поиск станет, наконец, целенаправленным, осмысленным и эффективным. Стоит отметить, что в диэлектриках и полупроводниках, в отличие от металла, свету, возможно, всё же приходится совершать некоторую работу по ионизации атомов, поскольку производится отрыв уже не только внешних, но, порой, и внутренних электронов в атоме. Вероятней всего, в таких случаях свет не сам выбивает эти внутренние электроны, а делает это через посредство внешних. Сначала свет воздействует на внешние, крутящиеся возле атома электроны энергии E=hf, заставляя их срываться с орбиты (§ 4.3). Эти внешние электроны ударяют в другие атомы и, при достаточной энергии E (если она достигает энергии ионизации E_и), выбивают из атомов внутренние электроны, производя ионизацию. В этом, видно, и состоит причина того, что атом может быть ионизован лишь светом частоты f=E_и/h или большей. Поэтому, фотоэлементы и солнечные батареи необходимо конструировать на основе материалов с возможно меньшей энергией отрыва электронов от атомов.

Аналогично протекает фотоионизация в газах: внешние электроны атомов, сорвавшись с орбиты — под действием света частоты f=E_и/h, без потерь своей энергии E=E_и ударяют в другие нейтральные атомы и выбивают из них внутренние электроны, которым уже приходится преодолевать притяжение ядра, затрачивая на это сообщённую энергию E_и. Известна и многофотонная ионизация, когда ионизацию производит свет меньшей частоты f=E_и/nh, где n — целое число [74]. Однако, объясняется этот феномен, подобно нелинейному фотоэффекту, — не поглощением сразу n фотонов, а генерацией средой кратных частот 2f, 3f…, nf, за счёт нелинейных эффектов (§ 4.5). Интенсивное излучение частоты f, проходя через среду, обогащает свой спектр, за счёт генерации новых гармоник атомами газа. Это вторичное излучение кратных частот f'=nf=E_и/h и выбивает электроны из атомов. Впрочем, возможно и вырывание электрона из атома под действием ударов сразу нескольких фотоэлектронов (не фотонов!), с энергией, меньшей энергии ионизации.

Во многом схож с фотоэффектом и процесс образования электрон-позитронных пар, под действием гамма-излучения, тоже имеющего критическую частоту f=E_п/h, по превышении которой из ядер вырываются электроны с позитронами [139]. Только здесь энергия E_п — это уже не энергия связи электронов с металлом или с атомом (энергия ионизации), а электростатическая энергия связи электронов и позитронов в ядре, составляющая величину, порядка E_п=2mc² (§ 1.16, § 3.12, § 3.13). В целом, процесс "рождения" электрон-позитронных пар протекает подобно фотоионизации: излучение с частотой выше f>E_п/h воздействует на электрон, крутящийся в магнитном поле ядра, с той же частотой f и энергией E=hf>E_п. Этот электрон, при ударе о ядро, способен за счёт своей высокой энергии выбить из ядра либо электрон, либо позитрон, которых в ядрах почти поровну. Оттого гамма-излучение и создаёт поток, где электронов и позитронов поровну, что трактуют как рождение их парами. Впрочем, нередко они и впрямь вылетают парами, если электрон, выбивший позитрон, не поглотится ядром, а отскочит от него. Тогда, в камере Вильсона видно, как из одной точки (от одного ядра) исходят сразу два следа: электрона и позитрона. Если вспомнить аналогию электронов и позитронов — с чёрными и белыми шашками, сидящими в своих клетках на шахматной доске (атомном ядре, § 3.2, § 3.12), то механизм вылета из ядра электрон-позитронных пар напоминает игру "Чапаев", где удары чёрных шашек (электронов) выбивают с шахматной доски белые шашки (позитроны), вылетающие нередко парой, вместе с ударившими их чёрными.

То, что ядра содержат позитроны, а удары электронов выбивают их оттуда, подтверждено явлением β⁺-распада и опытами Д. Скобельцына, в которых электрон-позитронные пары вылетали из ядер при облучении высокоэнергичными электронами [19, с. 326]. Если же энергия налетающего электрона или иной частицы (скажем, из космических лучей) — достаточно высока, то, при ударе о ядро, она может освободить до нескольких десятков электронов и позитронов. В этом случае, в камере Вильсона или на эмульсии видны "звёзды": из одной точки (ядра) исходят сразу сотни треков, — ядро как бы взрывается на сотни составлявших его элементарных зарядов (§ 3.9). Так же, и при облучении гамма-лучами с частотой f>>E_п/h образуются высокоэнергичные электроны, выбивающие из ядра сразу несколько электрон-позитронных пар. Понятно и то, почему число образуемых пар пропорционально квадрату заряда ядра Z². Ведь, в ядрах с высоким Z— пропорционально Z² увеличено число электронов, крутящихся в магнитном поле ядра — на соответствующих орбитах, с энергией порядка 1 МэВ. Значит, гамма-излучение в Z² раз эффективней воздействует на вещество, вырывая эти электроны и, при ударе их о ядра, порождая больше электрон-позитронных пар.

Итак, опыт убеждает, что все так называемые "квантовые закономерности", открытые в явлениях фотоэффекта, фотоионизации и рождения электрон-позитронных пар, обусловлены отнюдь не свойствами света, но — свойствами атомов, вещества. Так, селективный и нелинейный фотоэффекты явно свидетельствуют, что процессы излучения и поглощения веществом света имеют резонансный, колебательный, волновой характер, а никак не квантовый. Лишь классическая модель фотоэффекта, которую отстаивал и отец фотоэффекта А. Столетов, способна помочь адекватному и простому пониманию всех закономерностей фотоэффекта.

Эффект Комптона

Явление изменения длины волны при рассеянии света можно было бы объяснить с волновой точки зрения при помощи явления Доплера: электроны, рассеивающие рентгеновские лучи, под действием их выбрасываются из атомов по различным направлениям с разными скоростями. Таким образом, рассеянное излучение должно иметь изменённую длину волны в зависимости от скорости и направления движения рассеивающих электронов. Вычислив, как должны были бы двигаться рассеивающие электроны, нетрудно получить классическую картину явления Комптона.

Г.С. Ландсберг, "Оптика" [74]

Не составит большого труда объяснить с классических позиций и другое "квантовое" явление — эффект Комптона, который вместе с фотоэффектом считают неопровержимым доказательством фотонной теории. Суть его в том, что рентгеновские лучи претерпевают на электронах так называемое "комптоновское рассеяние" (Рис. 157). Причём, в отличие от обычного рассеяния, длины волн падающего λ₀ и рассеянного λ' излучения не совпадают, а их разница жёстко связана с углом рассеяния θ соотношением

λ'—λ₀= 2λ_кsin²(θ/2),

где λ_к — комптоновская длина, составляющая для электрона массы m величину λ_к=h/mc= 2,4·10^–12 м [134]. Кроме того, как показали опыты, электрон в процессе рассеяния испытывает отдачу, приобретая скорость, направленную под таким углом φ к падающему лучу, что tgφ= ctg(θ/2)/(1+λ_к/λ₀). Всё выглядит так, словно не волна рассеивается на электроне, а с ним упруго сталкивается частица, фотон, передающий электрону часть своего импульса и энергии. К тому же, как утверждают многие учебники, классическое взаимодействие волны с электронами вещества не могло бы породить рассеянного излучения на смещённой частоте. Ведь свободный электрон, по теории Дж. Томсона, должен колебаться под действием электромагнитной волны — с частотой поля этой волны, а, значит, и излучение испускать — на той же частоте и с той же длиной волны λ₀ [82]. А, между тем, рассеянное излучение в эффекте Комптона, кроме несмещённой компоненты спектра λ₀, содержит сдвинутую, — с длиной волны λ'.

Рис. 157. Эффект Комптона.

Кроме того, совсем как в фотоэффекте, в комптоновском — скорость и энергия электрона часто превосходят те, которые ему могла бы сообщить волна в момент облучения [134]. Это, опять же, трактуют как соударение с электронами световой волны, собранной в порции, кванты. Но, в действительности, похоже, и здесь луч не отдаёт электронам энергию, а лишь высвобождает электроны, изначально обладавшие скоростью в атомах. Поэтому, никто ещё не смог наблюдать комптоновское рассеяние на свободных электронах. Учёные признают, что его дают только электроны атомов, но полагают, что атом, испустивший электрон, — это лишь досадная помеха и электроны в нём можно рассматривать как свободные. На самом же деле, без участия атомов комптон-эффект был бы вовсе невозможен, его никто и никогда не сможет наблюдать у свободных электронов. Так, в случае обратного комптон-эффекта, когда уже действительно свободно летящий электрон не поглощает, а, напротив, отдаёт энергию свету, имеет место лишь классическое рассеяние [151, с. 312]. Далее покажем, что и прямое комптоновское рассеяние имеет чисто классические причины.

Собственно говоря, некоторые учёные даже проговорились, что такое объяснение существовало, но было основательно забыто. Так, Г.С. Ландсберг пишет, вопреки часто приводимому в учебниках утверждению, по которому классическая теория не способна объяснить рассеяния на новой частоте, что реально и классика предсказывает смещённые компоненты излучения. Ведь, если учесть, что электроны, вылетающие из атомов под действием внутреннего фотоэффекта, обладают большими скоростями, то рассеянное ими излучение, по эффекту Доплера, обязано иметь иную длину волны [74]. Эта длина волны λ', в полном согласии с комптон-эффектом, будет зависеть от длины волны λ₀ падающего излучения, от угла вылета электрона и направления рассеянного излучения. Так возникает классическая картина эффекта Комптона. Ландсберг не раскрывает подробностей этого описания и того, кто его автор. Поэтому попробуем реконструировать, восстановить эту забытую трактовку, отреставрировав классическую картину явления.

Пусть электромагнитная волна частоты f₀, падая на атом, "вырывает" из него электрон, имеющий, как показывает фотоэффект (§ 4.3), энергию mV²/2= hf₀. Угол φ вылета электрона может оказаться любым. Падающая волна заставит этот свободно летящий со скоростью V электрон колебаться, но, в силу эффекта Доплера, — с частотой f=f₀(1+Vcosφ/c), отличной от f₀ (Рис. 158). Вибрирующий электрон излучает вторичные волны, частота прихода f' которых, в некотором направлении θ,— отлична от частоты их испускания f. Из эффекта Доплера f'=f(1+Vcos(φ+θ)/c)=f₀(1+Vcosφ/c)(1+Vcos(φ+θ)/c). Кроме того, падающая волна заставит колебаться и излучать с частотой f₀ электроны, оставшиеся в атоме. Эти две волны от атома и свободного электрона интерферируют, но правильно сложиться не могут, поскольку их частоты f₀ и f' не совпадают. Во всех направлениях эти две волны сложатся беспорядочно, создавая биения, или вообще не сложатся от несинхронного прихода. И, лишь в направлении θ, для которого f₀= f'= f₀(1+Vcosφ/c)(1+Vcos(φ+θ)/c), волны интерферируют за счёт равенства частот и одновременного прибытия, откуда cosφ= —cos(φ+θ), то есть φ=90°-θ/2.

Рис. 158. Механизм комптон-эффекта: излучение f₀, "вырывая" электрон из атома, рассеивается им с частотой f'.

Подставляя значение φ, найдём, что лучи, идущие в направлении θ, имеют частоту

f'= f₀(1–Vsin(θ/2)/c)(1+Vsin(θ/2)/c)=f₀(1–sin²(θ/2)V²/c²)

и длину волны

λ'= с/f'= λ₀+ λ₀sin²(θ/2)V²/c².

Учтя же, что для излучения, выбившего электрон, λ₀=c/f₀=2hc/mV², найдём

λ'= λ₀+ sin²(θ/2)2h/mc.

То есть, пришли к проверенной опытом формуле λ'—λ₀= 2λ_кsin²(θ/2), где λ_к= h/mc. Также приходим к правильному соотношению углов рассеяния и отдачи, ибо если φ =90°- θ/2, то tgφ = ctg(θ/2). Это довольно точно совпадает с опытно проверенной зависимостью tgφ = ctg(θ/2)/(1+λ_к/λ₀), поскольку λ_к= 2,4·10^–12 м обычно много меньше длины волны λ₀ рентгеновского излучения, диапазон которого простирается от 10^–7 до 10^–12 метра. Лишь для самых жёстких рентгеновских лучей величина (1+λ_к/λ₀) будет заметно отличаться от единицы. Но тогда надо, соответственно, уточнить и наш приближённый расчёт, ибо при сопоставимости λ_к= h/mc и λ₀=2ch/mV² скорость V электрона становится сравнимой со скоростью света c, и в выражении для f' надо учесть квадратичный эффект Доплера (§ 1.20). При расчёте сделан и ряд других упрощений, конечно, не меняющих сути дела, поскольку более строгий классический анализ, учитывающий отдачу атома при испускании электрона, взаимодействие с волной обратного рассеяния и условие волнового синхронизма, даёт ту же картину эффекта Комптона.

Отметим ещё одно отличие квантовой и классической теории комптон-эффекта. В квантовой теории свет (фотон) излучается лишь в плоскости, образуемой лучом света с линией движения электрона. А в классической картине рассеянный свет излучается во всех направлениях вдоль образующих конуса, ориентированных под углом φ+θ к линии движения электрона (оси конуса), поскольку для всех этих направлений выполнено условие интерференции лучей. Однако, наиболее интенсивное излучение испускается всё же под углом θ к исходному лучу. Дело в том, что электроны, вылетающие под углом φ к оси луча и создающие излучение соответствующей длины волны λ'=λ₀+ sin²(θ/2)2h/mc, могут лететь не только вверх, но и вбок, и вниз, вдоль образующих конуса с углом φ и осью луча. Все эти электроны формируют свои конусы излучения, которые, складываясь, дают усреднённую картину. Касательная поверхность к этим конусам даёт каустическую поверхность, вдоль которой излучение наиболее интенсивно. Эта поверхность имеет форму конуса, с углом при вершине θ и осью, совпадающей с исходным лучом. Таким образом, хотя рассеяние происходит во всех направлениях, наиболее интенсивное излучение света длины волны λ'=λ₀+ sin²(θ/2)2h/mc идёт под углом θ, где θ=180°-2φ. Именно это обнаружилось в опыте. Причём, комптоновское излучение λ' действительно исходит не только в направлении θ, но и под другими углами, просто с меньшей интенсивностью. Поэтому, на спектрограммах, для данного угла θ, видно излучение не только на длине волны λ'=λ₀+ sin²(θ/2)2h/mc, но и на соседних длинах волн [134], чего квантовая теория объяснить не может.

Чтобы проверить, какая из теорий эффекта Комптона (квантовая или классическая) справедлива, достаточно исследовать эффект Комптона на свободных электронах, скажем летящих в вакуумных лампах или в электронно-лучевых трубках. Если эффект Комптона при этом будет наблюдаться, то справедлива квантовая теория явления. Если же он не обнаружится или будет слишком слаб, то квантовая теория ошибочна, а справедлива классическая теория, по которой лишь электроны, вылетающие из атомов, способны создавать комптон-эффект. Различить, рассеивается ли свет свободными электронами или остаточными атомами в колбе, можно по известной скорости электронов в лучевых трубках. Эта скорость внесёт известный доплеровский сдвиг в положения спектральных линий комптоновского излучения.

Было проведено много экспериментов по измерению энергий электронов в эффекте Комптона, углов испускания излучения, проверки синхронности испускания излучения и электронов [82, 134]. Все они подтвердили справедливость квантовой картины эффекта Комптона. Однако та же картина, как показано выше, должна возникать и в классическом случае, только объяснение будет совсем иным. То есть, эксперименты никоим образом не подтверждают квантовой трактовки комптон-эффекта, а, зачастую, и противоречат ей, подтверждая скорее классическую картину явления, если учесть ряд опытно выявленных особенностей эффекта Комптона.

Выходит, фотоэффект и эффект Комптона, — эти два главных свидетельства в пользу фотонной теории и корпускулярно-волнового дуализма, оказались ничтожны: световую волну ни к чему считать фотоном, частицей. Не существует опытов, для истолкования которых нужны кванты света. Введение фотонов, в то время как все свойства света легко объяснить классическими волнами, — это то самое преумножение сущностей, против которого предостерегал Оккам. Два фундаментальных эффекта, — фотоэффект и эффект Комптона, на которых держалось всё здание квантовой физики, как оказалось, вполне можно интерпретировать в рамках классической физики, причём столь удачно, что удалось объяснить ряд особенностей, проблемных для квантовой физики. В итоге, фотоны и кванты света оказываются не просто избыточными, ненужными, но и вредными для адекватного понимания сути явлений. Ведь неклассические, дуалистические объяснения — не материалистичны (§ 4.13, § 5.12). Не случайно, по своим взглядам А. Комптон был как раз сторонником физического идеализма, поскольку пытался в рамках физики развивать нематериалистические идеи релятивизма [29, с. 20], говорящего об отсутствии объективной реальности и относительности понятия "частица" и "волна".

Мы многое знаем о Комптоне, но, к несчастью, ничего не можем сказать о том Неизвестном Учёном, который, как следует из "Оптики" Ландсберга, предложил классическую трактовку комптон-эффекта. В этом плане учебник Ландсберга, вообще, — весьма примечателен и заслуживает пристального внимания. Сознательно или случайно в него были внесены многие верные идеи, или упоминания о них, пусть и в критическом ключе. Это и изложение сути БТР, и упоминание классической модели атома Ритца, а также ажурной модели атома Ленарда (прообраза ядерной модели Резерфорда), и интересные замечания о нелинейном, селективном фотоэффекте, наконец, — классическая трактовка эффекта Комптона. Будучи тесно связан с оптическими проблемами, Г.С. Ландсберг, по-видимому, имел доступ к закрытым источникам информации, располагал и интересовался многими сокрытыми данными об идеях и личностях, забытых в кванторелятивистской горячке. Но и целой книги не хватит, чтобы всех их перечислить, рассказать об их жизни и заслугах. Сколько было таких безвестных учёных-героев, осмелившихся, вопреки общему мнению и хору глупцов-подпевал неклассической физики, усомниться в кванторелятивистской картине мира и выдвинуть свои альтернативные идеи? Сколько таких великих, порой бесценных идей погибло по вине чьих-то амбиций, злой воли, зависти и корысти? Сколько таких безвестных учёных было замучено в застенках институтов — травлей сворой академиков, террором научной мафии, запретами на публикации в журналах? Сколько их, ищущих и бескорыстно служащих истине, безвестно умерло, не успев донести до нас свои светлые мысли? Но не их имена произносят с уважением, а имена их мучителей и попирателей истины. И не стоит ли, раз существует Могила Неизвестного Солдата, почтить память Неизвестного Учёного, Борца за классическую науку и свободу мысли, подобным памятником? Также, все усилия следует приложить и к тому, чтобы восстановить, реконструировать имена и идеи этих учёных, самозабвенно отдавших жизнь борьбе за истину, против мракобесия в науке. Они достойны памяти и уважения не меньше, чем герои войны.

Опыт Франка-Герца

Когда разность потенциалов достигнет 4,9 В, электроны при неупругом столкновении с атомами ртути вблизи сетки отдадут им всю свою энергию… Аналогичные опыты в дальнейшем были проведены с другими атомами. Для всех них были получены характерные разности потенциалов, называемые резонансными потенциалами.

А.Н. Матвеев, "Атомная физика" [82]

Итак, энергия не излучается и не поглощается атомом в виде фотонов, квантов света. Нет "квантовых явлений", которые нельзя бы было истолковать в рамках классической физики. Но и внутри атомов энергия электрона не квантуется, не меняется дискретно, вопреки квантовой механике. Дискретное изменение энергии в атоме обычно доказывают дискретным спектром атомов (излучаемый атомом спектр частот создаётся, якобы, переходами между постоянными уровнями энергии) и опытом Франка-Герца. Как помним, дискретный спектр излучения связан, в действительности, не с уровнями энергии, а с наличием у электронов собственных частот колебаний в магнитном поле атома (§ 3.1). Поэтому, и опыт Франка-Герца, видимо, связан с этими резонансными частотами атома. В этом опыте выяснилось, что атомы поглощают энергию порциями [82, 134]. Это следовало из того, что электроны, разгоняемые электрическим полем, при столкновении с атомами, — отдавали им свою энергию E, едва она достигала значения E₁, равного первому резонансному потенциалу атома (минимальной энергии электрона необходимой для возбуждения атома). Уже само упоминание резонанса говорит о том, что потеря электроном энергии вызвана совпадением частот. В самом деле, электрон с энергией E, столкнувшись с атомом, либо отскочит, либо на время с ним соединится, угодив в магнитную ловушку атома и начав обращаться с частотой f=E/h. Повращавшись в обществе атома, он может его покинуть, сохранив свой запас энергии.

Но всё будет иначе, если частота обращения f этого внешнего электрона совпадёт, войдёт в резонанс с частотой собственных колебаний одного из внутренних электронов, сидящих в узлах атома (Рис. 159). Тогда, внешний электрон, кружась, станет своим периодичным воздействием, при регулярном сближении, сильно раскачивать узловой, и, передав ему свою энергию, покинет атом — с заметно меньшим её запасом. А колеблющийся, внутренний электрон начнёт постепенно терять энергию в виде излучения с частотой f своего кружения в узле, пока не замрёт там. Вот почему, едва электроны наберут в ускоряющем поле критическую энергию E₁, они сразу её теряют, вызывая свечение газа на частоте f=E₁/h первой резонансной линии [134].

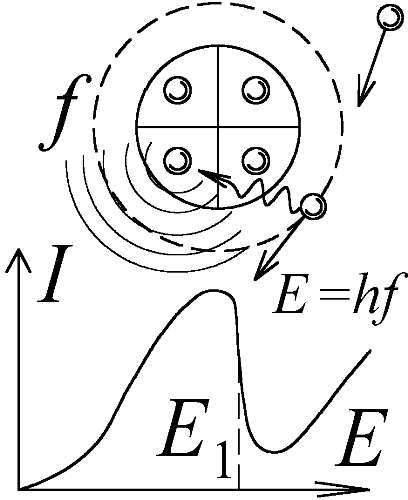
Рис. 159. Опыт Франка-Герца: уход энергии электрона в излучение при резонансе.

Отметим, что в случае, если энергия захваченного электрона больше резонансного потенциала, он уже не сможет возбудить колебания внутреннего электрона, поскольку будет вращаться с большей частотой. Усовершенствованный опыт Франка-Герца, действительно, показал, что если электрон влетает в газ уже с энергией, большей резонансного потенциала, он эту энергию не теряет, и ток электронов не снижается [134]. Это ещё раз доказывает резонансный характер явления: атом не может забрать энергию у электронов не только с энергией, меньшей критической, равной резонансному потенциалу, но и с большей. В противоположность этому, ионизацию атома, отрыв от него электрона, как показали опыты, способны производить и электроны с энергией, большей потенциала ионизации E_и. Это соответствует классической теории, поскольку в отличие от возбуждения излучения, ионизация атома вызывается чисто механическим ударом электрона по атому. Но это явление ударной ионизации — в корне противоречит квантовой теории атома Бора, по которой атом, с его дискретной системой уровней, способен поглощать только строго определённые порции энергии, как при возбуждении, так и при ионизации.

Впрочем, кванторелятивисты выдумали следующую уловку. Если электрон имеет энергию E, большую потенциала ионизации E_и, то его энергия может быть поглощена атомом, независимо от значения E, поскольку выше E_и спектр энергий атома становится из дискретного — сплошным, так как энергия электрона вне атома может быть произвольной [134]. Это якобы подтверждает и то, что линейчатый спектр излучения атома становится сплошным — после достижения границы серии f_∞ (так, у водорода это частота f_∞=Rc(1/n²–1/m²)=Rc/n², для которой m=∞ [74]). Но это, именно, — уловка, ибо она противоречит постулату Бора о порционном захвате энергии атомом. Ведь электроны вне атома уже не имеют отношения к его энергетическому спектру, и надо отдельно рассматривать дискретные скачки энергии электрона внутри атома и непрерывные её вариации уже после ионизации и поглощения энергии E_и. То есть, квантовая трактовка не проходит, зато классическая легко объясняет как ионизацию, так и сплошной спектр, примыкающий к границе серии. Сплошной спектр генерируют электроны, захваченные магнитным полем атома, когда крутятся в нём с частотой f=E/h и излучают на этой частоте (§ 3.1). От излучения их энергия E убывает, и плавно снижается частота f излучения электрона, по мере расширения витков его орбиты. Так атом генерирует сплошной спектр. Но, едва частота вращения f снизится до значения f_∞ (до предельной частоты излучения в спектральной серии), как внешний электрон, за счёт резонанса, станет быстро отдавать свою энергию внутренним, узловым электронам (с собственными частотами ~f_∞), как в опыте Франка-Герца. Поэтому, внешний электрон, отдав им энергию и потеряв скорость, уже не удерживается силой Лоренца. Он отрывается от атома, перестав вращаться и излучать, а генерируемый им сплошной спектр обрывается на границе серии f_∞.

Тем самым, ещё один фундаментальный опыт, доказывающий будто бы, что энергия излучения и электрона в атоме квантуется, принимая лишь дискретный ряд значений, как оказалось, можно легко истолковать с классических позиций, если принять магнитную модель атома Ритца. Энергия электрона в атоме меняется непрерывно, а мнимая дискретность вызвана связью частоты колебаний электрона и его энергии, а, также, — дискретным рядом частот, которые может излучать атом из-за дискретного распределения в нём узловых электронов. Возможно, поэтому многие учебники избегают упоминаний о резонансных потенциалах, наводящих на мысль о резонансе частот, и говорят о них как о критических потенциалах или потенциалах возбуждения.

Лазеры и квантовая электроника

Никто не оспаривает тот факт, что я сделал первый лазер… Если они сделали это, то где же тогда, чёрт возьми, их лазер?

Теодор Мейман об учёных-кванторелятивистах

Лазеры стали важнейшей составляющей современной науки, техники и быта. Поэтому особенно обидно, что эти генераторы света, вопреки идеям их создателей, называют квантовыми генераторами, а саму лазерную физику — квантовой электроникой. На деле, лазерное излучение, как видели (§ 4.5), не стоит связывать с квантами и фотонами, ведь лазер — это просто высокодобротный оптический резонатор и усилитель, который избирательно усиливает одни волны и гасит другие, подобно акустическому, выделяя заданные частоты и фазы колебаний. Происходит, по сути, такая же, как в опыте Франка-Герца, перекачка энергии, запасённой во внешних электронах атома, частота колебаний которых не фиксирована и превышает основную частоту f, — к узловым, внутренним электронам, колеблющимся и излучающим на этой стандартной частоте f. Именно это и позволяет трансформировать разные виды энергий накачки — в когерентный свет, с его жёстко заданной фазой и частотой. А стандарт этой частоты задан отнюдь не квантами и дискретными значениями энергии атома, а кристально чёткой пространственной структурой атома, с твёрдым масштабом расстояний и констант радиуса r₀, магнитного момента μ и заряда e электрона (§ 3.1).

Лазер — это чисто классический прибор, в котором происходит нелинейное взаимодействие электромагнитных волн и колебаний атомных электронов. За счёт этого, энергия электронов, вибрирующих с разными частотами и фазами, и преобразуется в энергию колебаний электронов на стандартной частоте f лазерного излучения. Этот процесс уже давно описан в классической, хоть и нелинейной теории колебаний [103], а фотонами и квантами здесь, как говорится, "и не пахло". Сначала оптическое излучение накачки (скажем, от лампы-вспышки) возбуждает колебания внешних и внутренних электронов атома на множестве собственных частот, причём на некоторой частоте f колебания возбуждаются особенно эффективно. Электроны, вибрирующие с частотойf, теряют энергию медленней, чем получают её от взаимодействия с другими электронами и излучёнными ими волнами. Поэтому, при некоторой интенсивности излучения, превышающей пороговую, колебания электронов на частоте f будут усиливаться, за счёт энергии всех прочих колебаний, переходящей в энергию колебаний и излучения на основной частоте f.

Как следует из соотношений Мэнли-Роу [103], такая перекачка энергии эффективна лишь в случае, если высокочастотное излучение преобразуется в низкочастотное. Вот почему, излучение накачки обязательно должно иметь частоту f_p — большую, чем частота f излучения лазера, хотя здесь играет роль и постепенное расширение витков орбиты внешних электронов, передающих свою энергию узловому электрону, при снижении частоты их колебаний с f_p до f. То есть, здесь ни при чём обычное объяснение, по которому энергия кванта излучения лазера E=hf не может быть больше энергии кванта накачки E_p=hf_p. Совершенно излишне здесь и представление об инверсии населённостей уровней атома, ибо порог генерации задаётся балансом скорости притока и оттока энергии основных колебаний электронов на частоте f. Так что, "квантовые" генераторы и усилители работают исключительно по классическим принципам теории колебаний и волн, не требуя квантовых. В некоторых типах лазеров, например в полупроводниковых, газовых и некоторых других, механизм перекачки энергии может иметь и более сложный, но, всё равно, — классический характер. В этих случаях, генерация лазерного излучения может идти примерно так. При накачке (скажем электрическим разрядом) атомы, а, точнее, — их внешние электроны, набирают энергию. Одновременно возбуждаются и внутренние электроны в узлах, которые генерируют пока ещё некогерентное, но уже имеющее стандартную частоту f излучение (могут присутствовать и другие частоты спектра, которые усиливаются и излучаются гораздо хуже).

Это излучение, проходя сквозь атомы, заставляет их, по спусковому механизму фотоэффекта, выбрасывать те внешние электроны, что крутятся с той же частотой f (в отличие от внутренних электронов, они излучают очень слабо, поскольку имеют гораздо меньшие значения скоростей и ускорений, § 3.2). Тогда, атом испытывает отдачу, отчего происходит взбалтывание его узловых электронов, особенно электронов с частотой собственных колебаний f, так же как в опыте Франка-Герца. Поэтому, они сами начинают генерировать излучение f, причём, — в той же фазе, что и падающий свет, поскольку их колебания запущены синхронным с падающей волной внешним электроном (Рис. 160). Его рывок-отдача не только запускает колебания внутреннего электрона, но и синхронизует их с падающим светом.

Рис. 160. Генерация лазерного света: набор электроном энергии в поле E разряда, его захват и выброс атомом от фотоэффекта.

Таким образом, запальное излучение будет лавинно нарастать, за счёт энергии внешних электронов. Спустя время те восполнят утерянную при вылете энергию, за счёт устройства накачки, затем поглотятся атомами и снова будут испущены при падении волны. Итак, каждый акт усиления начального излучения связан с выбросом и захватом электрона. Недаром, наибольшим КПД и распространением обладают разработанные отечественными физиками Г. Алфёровым и Н.Г. Басовым полупроводниковые лазеры (те, что стоят в СD- и DVD-устройствах), где инжекционная генерация света напрямую связана с внутренним фотоэффектом. Это доказывает тесную связь лазерного излучения с прямым и обратным фотоэффектом — с элементарными актами испускания-поглощения электронов и света атомами среды. Не зря, и сам фотоэффект Планк уподоблял взрывному, лавинному процессу, где свет лишь высвобождает запасённую энергию, служа спусковым механизмом лавины (§ 4.3). Вообще, лазер стали применять в качестве оружия отчасти потому, что его работу издавна иллюстрируют с помощью баллистической аналогии. В лазере атомы сначала запасают энергию, как запасает её тетива лука, арбалета, баллисты, или заряд пороха в ружье, а после энергия взрывообразно высвобождается спусковым крючком, которым в лазере служит сам свет.

В квантовой же физике объяснение генерации лазерного света звучит крайне неправдоподобно. Достаточно сказать, что основное свойство лазерного излучения — его когерентность, равенство частот и фаз у всех волн света, — там объясняют, не рассматривая сами волны и их генерацию, а рассуждая исключительно о фотонах и квантах света, — о неволновой стороне явления. И, вообще, ошибочно считать, что создание лазеров чем-то обязано квантовой теории. Лазеры изначально были разработаны исключительно на основании известного из опытов оптического свойства сред, — способности возбуждённых атомов среды излучать свет заданной частоты под действием падающего света (сугубо классического эффекта фотолюминесценции, § 3.1). Поэтому, первые лазеры были изобретены и построены техниками, инженерами, экспериментаторами, людьми далёкими от квантовой и вообще теоретической физики (так же и первый мазер был построен Басовым и Прохоровым, на основе классической молекулярной радиоспектроскопии и нелинейной теории колебаний). Первые подвижки в этом направлении и, даже, реально работающие лазеры были сделаны ещё в XIX веке инженером-изобретателем Н. Тесла, позднее крайне негативно относившимся и к теории относительности, и к квантовой физике. Созданная им в 1890 г. электронная лампа давала свет по механизму, близкому к генерации монохроматичного света в опыте Франка-Герца (§ 4.8) и уже имела зеркальный резонатор с полупрозрачным участк<