
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Методы одномерной нелинейной оптимизации с использованием производных
Задачи оптимизации.
Можно выделить два типа задач оптимизации — безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (1.1) при действительных переменных и определении соответствующих значений аргументов на некотором множестве σ n-мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный.
Условные задачи оптимизации, или задачи с ограничениями, это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве . Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
Ограничения-равенства выражают зависимость между, проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов т. п.
в результате ограничений область проектирования , определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи.
При наличие ограничений оптимальное решение может соответствовать либо локальному экстремуму в нутрии области проектирования, либо значению целевой функции на границе области. Если ограничения отсутствуют то ищется оптимальное решение на всей области проектирования, то есть глобальный экстремум.
Одномерная линейная оптимизация. Основные понятия и определения. Методы решения задач одномерной оптимизации.
Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси: f(x) -> min ,
x принадлежит [a, b].
Максимизация целевой функции эквивалента минимизации ( f(x) -> max ) эквивалентна минимизации противоположной величины ( -f(x) -> min ), поэтому, не умаляя общности можно рассматривать только задачи минимизации.
К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того, необходимость в минимизации функций одной переменной возникает при реализации некоторых методов решения более сложных задач оптимизации.
Для решения задачи минимизации функции f(x) на отрезке [a, b] на практике, как правило, применяют приближенные методы. Они позволяют найти решения этой задачи с необходимой точностью в результате определения конечного числа значений функции f(x) и ее производных в некоторых точках отрезка [a, b]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.
Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(x) в заданных точках.
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке [a, b].
К методам решения задач одномерной оптимизации относятся прямые методы и методы с использованием производной. К прямым методам относятся: метод перебора, метод поразрядного поиска, метод дихотомии, метод «золотого сечения». К методам с использованием производной относятся: метод средней точки, метод хорд, метод Ньютона.

Предположим, отыскивается минимум функции 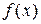 , расположенный на интервале
, расположенный на интервале  . В методе дихотомии при уточнении положения минимума пользуются следующей стратегией. Вычисляют значения функции в двух точках:
. В методе дихотомии при уточнении положения минимума пользуются следующей стратегией. Вычисляют значения функции в двух точках:
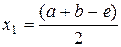 ,
,  ,
,
где е - малая величина, например, требуемая точность нахождения точки экстремума. Пусть оказалось, что 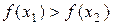 . Тогда точка минимума лежит на интервале
. Тогда точка минимума лежит на интервале 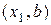 . Если же
. Если же 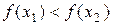 , то - на интервале
, то - на интервале 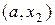 . Далее изложенный вычислительный алгоритм повторяется для найденного интервала расположения корня и так до тех пор, пока ширина интервала станет меньше
. Далее изложенный вычислительный алгоритм повторяется для найденного интервала расположения корня и так до тех пор, пока ширина интервала станет меньше 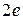 . Решением задачи будет середина заключительного интервала.
. Решением задачи будет середина заключительного интервала.
Более экономичным является метод золотого сечения. В основе этого метода лежит понятие «золотого сечения», введенного Леонардо да Винчи и используемого, в частности, при построении архитектурных сооружений античности и эпохи Возрождения.
В данном методе значения функции вычисляются в точке 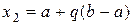 , делящей интервал
, делящей интервал  в отношении
в отношении 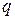 , и в точке
, и в точке 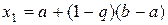 , симметричной точке
, симметричной точке  относительно середины интервала. При
относительно середины интервала. При 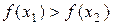 будет
будет  , если же
, если же 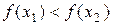 , то
, то 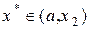 , где
, где 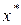 - минимум функции
- минимум функции 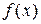 . Предположим оказалось, что
. Предположим оказалось, что 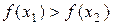 и
и  . Тогда, на второй итерации следует вычислять значения функции в точках
. Тогда, на второй итерации следует вычислять значения функции в точках
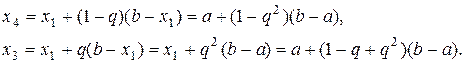
Выберем такое 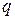 , чтобы
, чтобы 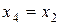 , следовательно
, следовательно  , откуда
, откуда 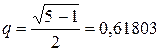 .
.
Деление отрезка в отношении 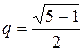 называют золотым сечением. Это дано название методу. Достоинство метода «золотого сечения» состоит в том, что на второй и последующих итерациях требуется вычисление только одного значения функции.
называют золотым сечением. Это дано название методу. Достоинство метода «золотого сечения» состоит в том, что на второй и последующих итерациях требуется вычисление только одного значения функции.
После каждой итерации происходит сужение интервала неопределенности расположения минимума в 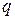 раз. Вычисления прекращаются, когда ширина интервала станет меньше
раз. Вычисления прекращаются, когда ширина интервала станет меньше 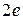 . Решением задачи считают середину интервала.
. Решением задачи считают середину интервала.
Пример. Найти минимум функции 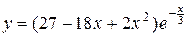 методом «золотого сечения» с погрешностью до
методом «золотого сечения» с погрешностью до  .
.
Локализуем минимум. С этой целью определим нули функции из уравнения 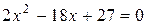 , решая которое находим
, решая которое находим 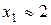 ,
, 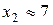 . Минимум функции обязательно расположен между ее нулями. Дальнейшее уточнение минимума осуществим, составив таблицу значений функции с шагом 0,5.
. Минимум функции обязательно расположен между ее нулями. Дальнейшее уточнение минимума осуществим, составив таблицу значений функции с шагом 0,5.
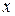
| 2 | 2,5 | 3,5 | ||
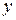
| -2,390 | -3,31 | -3,581 | -3,426 |
Заполнение таблицы прекращается после того, как происходит изменение поведения функции. До 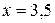 значения функции убывают, а затем начинают возрастать. Это значит, что экстремум функции расположен в окрестности этой точки. Принимаем
значения функции убывают, а затем начинают возрастать. Это значит, что экстремум функции расположен в окрестности этой точки. Принимаем 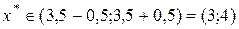 .
.
Уточняем расположение минимума, пользуясь методом золотого сечения. Вычисляем 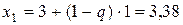 ,
, 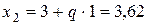 ,
, 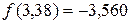 ,
, 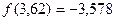 .
.
Имеем  , следовательно
, следовательно 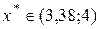 .
.
Вычисляем 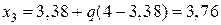 и
и 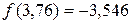 . Так как
. Так как 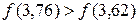 , то
, то 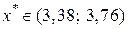 . Вследствие того, что ширина интервала
. Вследствие того, что ширина интервала 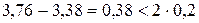 , процесс вычислений прекращаем и принимаем
, процесс вычислений прекращаем и принимаем
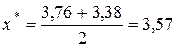 .
.
Линейное программирование
Основные понятия и определения. Общая задача линейного программирования






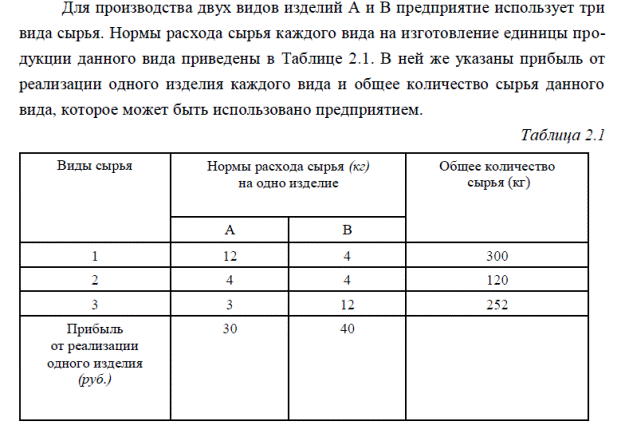
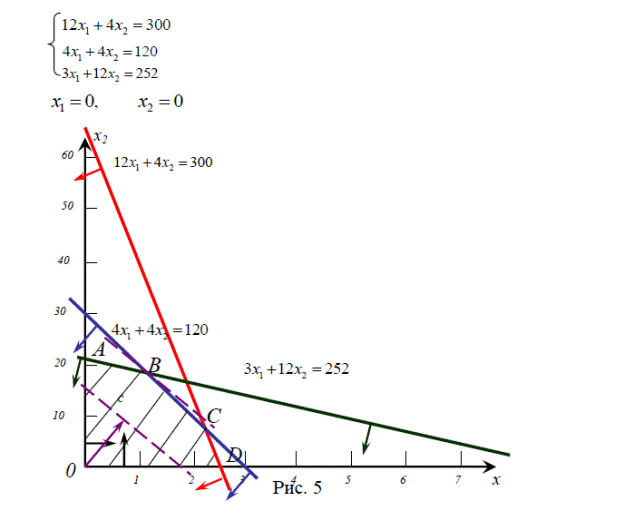
Пример 4


Элементы теории игр
Игры в чистых стратегиях. Основные понятия





| |
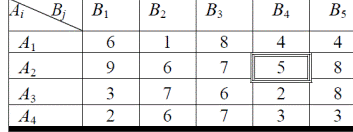
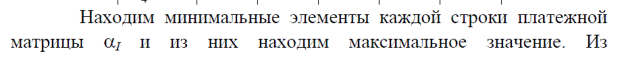

Пример



Пример


Задачи оптимизации.
Можно выделить два типа задач оптимизации — безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (1.1) при действительных переменных и определении соответствующих значений аргументов на некотором множестве σ n-мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный.
Условные задачи оптимизации, или задачи с ограничениями, это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве . Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.
Ограничения-равенства выражают зависимость между, проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов т. п.
в результате ограничений область проектирования , определяемая всеми проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи.
При наличие ограничений оптимальное решение может соответствовать либо локальному экстремуму в нутрии области проектирования, либо значению целевой функции на границе области. Если ограничения отсутствуют то ищется оптимальное решение на всей области проектирования, то есть глобальный экстремум.
Одномерная линейная оптимизация. Основные понятия и определения. Методы решения задач одномерной оптимизации.
Задачи одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси: f(x) -> min ,
x принадлежит [a, b].
Максимизация целевой функции эквивалента минимизации ( f(x) -> max ) эквивалентна минимизации противоположной величины ( -f(x) -> min ), поэтому, не умаляя общности можно рассматривать только задачи минимизации.
К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того, необходимость в минимизации функций одной переменной возникает при реализации некоторых методов решения более сложных задач оптимизации.
Для решения задачи минимизации функции f(x) на отрезке [a, b] на практике, как правило, применяют приближенные методы. Они позволяют найти решения этой задачи с необходимой точностью в результате определения конечного числа значений функции f(x) и ее производных в некоторых точках отрезка [a, b]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.
Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(x) в заданных точках.
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию f(x) унимодальной на отрезке [a, b].
К методам решения задач одномерной оптимизации относятся прямые методы и методы с использованием производной. К прямым методам относятся: метод перебора, метод поразрядного поиска, метод дихотомии, метод «золотого сечения». К методам с использованием производной относятся: метод средней точки, метод хорд, метод Ньютона.

Предположим, отыскивается минимум функции 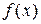 , расположенный на интервале
, расположенный на интервале  . В методе дихотомии при уточнении положения минимума пользуются следующей стратегией. Вычисляют значения функции в двух точках:
. В методе дихотомии при уточнении положения минимума пользуются следующей стратегией. Вычисляют значения функции в двух точках:
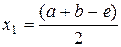 ,
,  ,
,
где е - малая величина, например, требуемая точность нахождения точки экстремума. Пусть оказалось, что 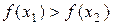 . Тогда точка минимума лежит на интервале
. Тогда точка минимума лежит на интервале 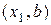 . Если же
. Если же 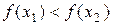 , то - на интервале
, то - на интервале 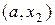 . Далее изложенный вычислительный алгоритм повторяется для найденного интервала расположения корня и так до тех пор, пока ширина интервала станет меньше
. Далее изложенный вычислительный алгоритм повторяется для найденного интервала расположения корня и так до тех пор, пока ширина интервала станет меньше 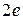 . Решением задачи будет середина заключительного интервала.
. Решением задачи будет середина заключительного интервала.
Более экономичным является метод золотого сечения. В основе этого метода лежит понятие «золотого сечения», введенного Леонардо да Винчи и используемого, в частности, при построении архитектурных сооружений античности и эпохи Возрождения.
В данном методе значения функции вычисляются в точке 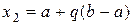 , делящей интервал
, делящей интервал  в отношении
в отношении 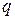 , и в точке
, и в точке 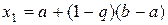 , симметричной точке
, симметричной точке  относительно середины интервала. При
относительно середины интервала. При 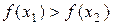 будет
будет  , если же
, если же 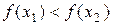 , то
, то 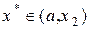 , где
, где 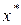 - минимум функции
- минимум функции 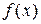 . Предположим оказалось, что
. Предположим оказалось, что 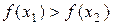 и
и  . Тогда, на второй итерации следует вычислять значения функции в точках
. Тогда, на второй итерации следует вычислять значения функции в точках
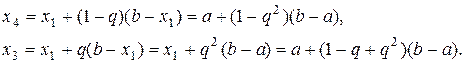
Выберем такое 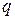 , чтобы
, чтобы 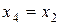 , следовательно
, следовательно  , откуда
, откуда 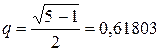 .
.
Деление отрезка в отношении 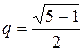 называют золотым сечением. Это дано название методу. Достоинство метода «золотого сечения» состоит в том, что на второй и последующих итерациях требуется вычисление только одного значения функции.
называют золотым сечением. Это дано название методу. Достоинство метода «золотого сечения» состоит в том, что на второй и последующих итерациях требуется вычисление только одного значения функции.
После каждой итерации происходит сужение интервала неопределенности расположения минимума в 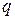 раз. Вычисления прекращаются, когда ширина интервала станет меньше
раз. Вычисления прекращаются, когда ширина интервала станет меньше 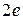 . Решением задачи считают середину интервала.
. Решением задачи считают середину интервала.
Пример. Найти минимум функции 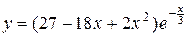 методом «золотого сечения» с погрешностью до
методом «золотого сечения» с погрешностью до  .
.
Локализуем минимум. С этой целью определим нули функции из уравнения 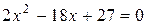 , решая которое находим
, решая которое находим 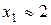 ,
, 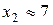 . Минимум функции обязательно расположен между ее нулями. Дальнейшее уточнение минимума осуществим, составив таблицу значений функции с шагом 0,5.
. Минимум функции обязательно расположен между ее нулями. Дальнейшее уточнение минимума осуществим, составив таблицу значений функции с шагом 0,5.
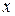
| 2 | 2,5 | 3,5 | ||
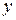
| -2,390 | -3,31 | -3,581 | -3,426 |
Заполнение таблицы прекращается после того, как происходит изменение поведения функции. До 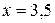 значения функции убывают, а затем начинают возрастать. Это значит, что экстремум функции расположен в окрестности этой точки. Принимаем
значения функции убывают, а затем начинают возрастать. Это значит, что экстремум функции расположен в окрестности этой точки. Принимаем 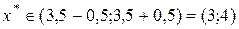 .
.
Уточняем расположение минимума, пользуясь методом золотого сечения. Вычисляем 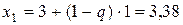 ,
, 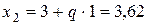 ,
, 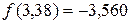 ,
, 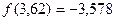 .
.
Имеем  , следовательно
, следовательно 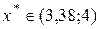 .
.
Вычисляем 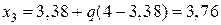 и
и 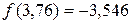 . Так как
. Так как 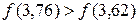 , то
, то 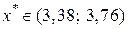 . Вследствие того, что ширина интервала
. Вследствие того, что ширина интервала 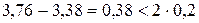 , процесс вычислений прекращаем и принимаем
, процесс вычислений прекращаем и принимаем
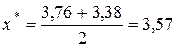 .
.
Методы одномерной нелинейной оптимизации с использованием производных



Метод Ньютона
Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений.
Пусть корень x* Î [a, b], так, что f '(a)f '(b) < 0. Положим x0 = b. Проведем касательную к графику функции y = f '(x) в точке B0 = (x0, f '(x0))
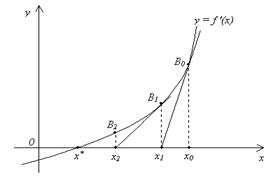
Уравнение касательной будет иметь вид:
y – f '(x0) = f"(x0)(x – x0). (1.16)
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е. положив в (1.16) y = 0, x = x1:
x1 = x0 – 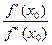 . (1.17)
. (1.17)
Аналогично поступим с точкой B1(x1, f '(x1)), затем с точкой B2(x2, f '(x2)), и т. д. в результате получим последовательность приближений x1, x2, …, xn , …, причем
xn +1 = xn – 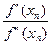 . (1.18)
. (1.18)
Формула (1.18) является расчетной формулой метода Ньютона.
При заданной точности e > 0 вычисления по формуле (1.18) нужно вести до тех пор, пока не будет выполнено неравенство | f '(xn)| £ e, после чего полагают x* » xn.
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...