Локальная и интегральная теоремы Лапласа

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

23. Нормальный закон распределения случайных величин. M(X), D(X), σ.

Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т.д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах её закон распределения.

Кривая распределения по нормальному закону имеет симметричный холмообразный вид . Максимальная ордината кривой, равная , соответствует точке 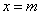; по мере удаления от точки плотность распределения падает, и при кривая асимптотически приближается к оси абсцисс.

Выясним смысл численных параметров и , входящих в выражение нормального закона (6.1.1); докажем, что величина есть не что иное, как математическое ожидание, а величина - среднее квадратическое отклонение величины . Для этого вычислим основные числовые характеристики величины - математическое ожидание идисперсию.

Применяя замену переменной

имеем:

(6.1.2)

Нетрудно убедиться, что первый из двух интервалов в формуле (6.1.2) равен нулю; второй представляет собой известный интеграл Эйлера-Пуассона:

. (6.1.3)

Следовательно,

,

т.е. параметр представляет собой математическое ожидание величины . Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно – ц. р.).

Вычислим дисперсию величины :

.

Применив снова замену переменной

имеем:

.

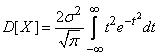Интегрируя по частям, получим:

.

Первое слагаемое в фигурных скобках равно нулю (так как при убывает быстрее, чем возрастает любая степень ), второе слагаемое по формуле (6.1.3) равно , откуда

.

24. Показательное (экспоненциальное) распределение. M(X), D(X), σ

Показательным (экспоненциальным) называетсяраспределение вероятностей непрерывной случайной величины X, которое описывается плотностью, имеющей вид

где λ –постоянная положительная величина

Функция распределения:

Вероятность попадания в интервал:

Математическое ожидание:

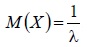
Дисперсия:

Среднее квадратическое отклонение:

25.Распределение Пуассона можно описать с помощью следующей математической модели. Пусть событие А происходит многократно с течением времени, то есть имеет место поток однородных событий, который удовлетворяет следующим условиям:

1) Поток стационарен, то есть вероятность попадания k событий в промежуток времени (t; t+τ) зависит только от числа событий k и длины промежутка τ, но не зависит от начала t. Это означает, что математическое ожидание числа событий в единицу времени (плотность потока) постоянно.

2) Поток без последствия, то есть вероятность попадания k событий в промежуток времени (t; t+τ) не зависит от числа и появления событий до момента времени t, то есть имеет место взаимная независимость появления того или иного числа событий в непересекающиеся промежутки времени.

3) Поток ординарен, то есть вероятность попадания двух и более событий в промежуток времени (t; t+τ) пренебрежимо мала по сравнению с вероятностью попадания одного события в этот промежуток, то есть вероятность одновременного появления двух и более событий равна нулю.

Поток событий, удовлетворяющий условиям 1)–3) называется простейшим. Плотность простейшего потока обозначим μ.

Вероятность того, что событие А в промежутке времени τ осуществится х раз, равна

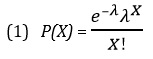где λ=μτ – среднее число событий, происходящих в промежутке времени τ

Числовые характеристики: МХ= DX=λ, σ(X)=

Распределение Стьюдента

Распределение хи-квадрат Случайная величина 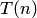есть отношение двух независимых случайных величин 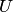и 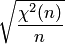, то есть

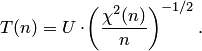
Распределение случайной величины 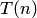называется распределением Стьюдента с степенями свободы. Его плотность задаётся формулой

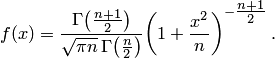
Математическое ожидание и дисперсия случайной величины, подчинённой распределению Стьюдента

, есть

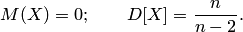
Как и в случае и хи-квадрат распределением, при увеличении распределение Стьюдента стремиться к нормальному, более того, стандартизованному нормальному (то есть с нулевым математическим ожиданием и единичной дисперсией). Распределение Стьюдента, как хи-квадрат распределение, широко применяется в задачах математической обработки измерений.

27. Распределение хи-квадрат. M(X), D(X), σ

Распределение Пирсона (хи - квадрат) – распределение случайной величины

где случайные величины X1, X2,…, Xn независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений.

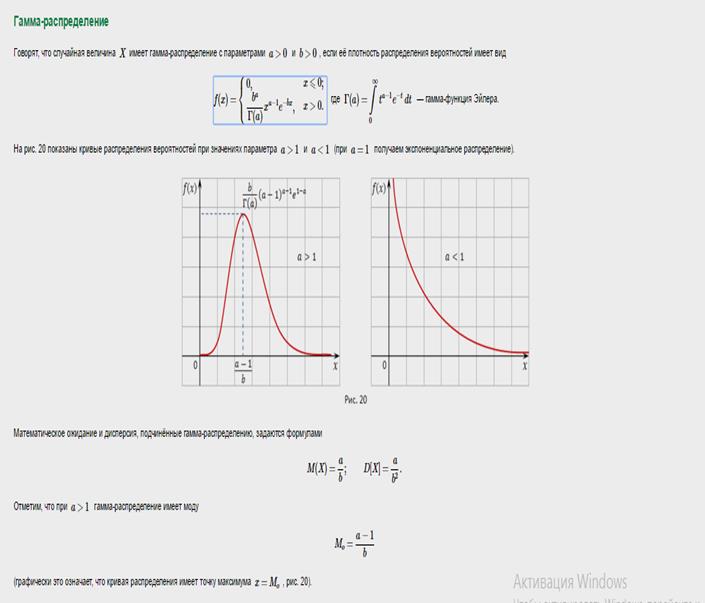28. Гамма распределение