
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
ВЕКТОРНОЕ ПОЛЕ. ВЕКТОРНЫЕ ЛИНИИ
Если в каждой точке  пространственной области
пространственной области 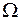 задан определенный вектор
задан определенный вектор 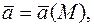 то говорят, что в этой области задано векторное поле. Векторное поле задается тремя скалярными функциями
то говорят, что в этой области задано векторное поле. Векторное поле задается тремя скалярными функциями 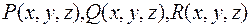 , являющимися проекциями вектора
, являющимися проекциями вектора  на координатные оси декартовой системы:
на координатные оси декартовой системы:
 .
.
Примерами векторных полей могут служить поле электрической напряженности, силовое поле, поле скоростей текущей жидкости и др. Векторное поле тоже может быть плоским, например,
 .
.
Векторной линией поля  называется такая линия, касательная в каждой точке которой направлена вдоль заданного в этой точке вектора поля (рисунок 1).
называется такая линия, касательная в каждой точке которой направлена вдоль заданного в этой точке вектора поля (рисунок 1).
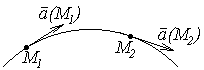
Рисунок 1
Всякое векторное поле  обладает семейством векторных линий. Уравнения этого семейства есть общее решение дифференциальных уравнений вида
обладает семейством векторных линий. Уравнения этого семейства есть общее решение дифференциальных уравнений вида
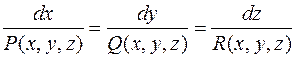 . (4)
. (4)
Задача 2. Для плоского поля 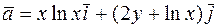 найти уравнения семейства векторных линий и векторной линии, проходящей через точку
найти уравнения семейства векторных линий и векторной линии, проходящей через точку 
Решение. Так как  то, согласно равенству (4), уравнение семейства одно и определяется общим решением дифференциального уравнения
то, согласно равенству (4), уравнение семейства одно и определяется общим решением дифференциального уравнения

 .
.
Это уравнение линейное относительно  как функции от
как функции от 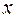 . Решая его методом вариации произвольной постоянной, получим общее решение в виде
. Решая его методом вариации произвольной постоянной, получим общее решение в виде
 .
.
Выделим из этого семейства одно решение то, которое представляет собой уравнение векторной линии, проходящей через точку 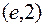 . Подставив в общее решение
. Подставив в общее решение  получим
получим 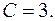 Итак, искомая векторная линия
Итак, искомая векторная линия 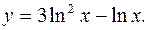
ПОТОК ВЕКТОРНОГО ПОЛЯ
Пусть в поле вектора 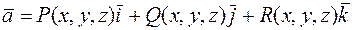 задана ориентированная поверхность
задана ориентированная поверхность  . Обозначим через
. Обозначим через  единичный вектор нормали к выбранной стороне поверхности в ее произвольной точке. Поверхностный интеграл первого рода по поверхности
единичный вектор нормали к выбранной стороне поверхности в ее произвольной точке. Поверхностный интеграл первого рода по поверхности  от скалярного произведения вектора
от скалярного произведения вектора  на вектор
на вектор 
 (5)
(5)
называется потоком векторного поля через ориентированную поверхность 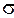 и обозначается
и обозначается 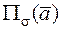 . В случае замкнутой поверхности
. В случае замкнутой поверхности  поток записывается в виде
поток записывается в виде
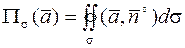 .
.
Если ввести в рассмотрение вектор  и обозначить его проекции на оси координат
и обозначить его проекции на оси координат 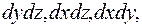 то формулу (5) можно переписать в виде
то формулу (5) можно переписать в виде
 (6)
(6)
где вектор  направлен по нормали к выбранной стороне поверхности
направлен по нормали к выбранной стороне поверхности  . Правая часть равенства (6) является поверхностным интегралом второго рода.
. Правая часть равенства (6) является поверхностным интегралом второго рода.
Если, например,  – поле скоростей текущей жидкости в области
– поле скоростей текущей жидкости в области 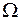 и
и  – незамкнутая поверхность с выбранным направлением нормали
– незамкнутая поверхность с выбранным направлением нормали  , то
, то 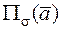 равен количеству жидкости, проходящей в единицу времени через поверхность
равен количеству жидкости, проходящей в единицу времени через поверхность  в направлении
в направлении  . Если
. Если  – замкнутая поверхность, ограничивающая некоторую область
– замкнутая поверхность, ограничивающая некоторую область 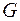 с внешней нормалью
с внешней нормалью  , то
, то 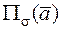 равен разности количеств втекающей в эту область жидкости и вытекающей. Когда
равен разности количеств втекающей в эту область жидкости и вытекающей. Когда  это означает, что в области
это означает, что в области 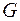 имеются источники (где векторные линии порождаются), а если
имеются источники (где векторные линии порождаются), а если 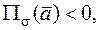 то это указывает на наличие в области
то это указывает на наличие в области 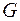 стоков (где векторные линии заканчиваются).
стоков (где векторные линии заканчиваются).
Если ориентированная поверхность  задана явно непрерывно дифференцируемой функцией
задана явно непрерывно дифференцируемой функцией  то по формуле (6) можно получить следующую формулу, связывающую поверхностный интеграл по поверхности
то по формуле (6) можно получить следующую формулу, связывающую поверхностный интеграл по поверхности  с двойным интегралом по проекции
с двойным интегралом по проекции 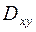 этой поверхности на плоскость
этой поверхности на плоскость  :
:
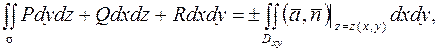 (7)
(7)
где знак плюс берется, когда интегрирование в левой части ведется по стороне  положительно ориентированной по отношению к оси
положительно ориентированной по отношению к оси  - вектор нормали к ориентированной поверхности. Запись
- вектор нормали к ориентированной поверхности. Запись 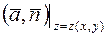 означает, что в произведении
означает, что в произведении  переменную
переменную 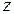 следует заменить на
следует заменить на 
Если поверхность  задана явно уравнением
задана явно уравнением 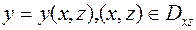 или
или  то соответственно меняются роли переменных в формуле (7).
то соответственно меняются роли переменных в формуле (7).
Замечание.Если поверхность  задана уравнением
задана уравнением  которое неоднозначно разрешается относительно одной из переменных и, следовательно, поверхность
которое неоднозначно разрешается относительно одной из переменных и, следовательно, поверхность  неоднозначно проецируется на соответствующую координатную плоскость (например
неоднозначно проецируется на соответствующую координатную плоскость (например  - цилиндрическая поверхность неоднозначно проецирующаяся на плоскость
- цилиндрическая поверхность неоднозначно проецирующаяся на плоскость 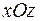 ), ее следует разбить на части, однозначно проецирующиеся на координатную плоскость.
), ее следует разбить на части, однозначно проецирующиеся на координатную плоскость.
Задача 3. Вычислить поток вектора  через нижнюю сторону поверхности
через нижнюю сторону поверхности  , отсеченной плоскостью
, отсеченной плоскостью  (рисунок 2).
(рисунок 2).

Рисунок 2
Решение. Учитывая, что  имеет различный знак
имеет различный знак  для правой и левой части поверхности
для правой и левой части поверхности 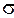 , а
, а 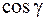 – сохраняет отрицательный знак для всей поверхности, будем иметь
– сохраняет отрицательный знак для всей поверхности, будем иметь

где  – правая часть поверхности (нормаль к ней составляет с
– правая часть поверхности (нормаль к ней составляет с 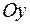 острый угол),
острый угол), 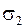 – левая часть поверхности. Первые два слагаемых уничтожаются, так как
– левая часть поверхности. Первые два слагаемых уничтожаются, так как  и
и 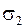 имеют одинаковую проекцию на
имеют одинаковую проекцию на 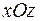 Окончательно имеем :
Окончательно имеем :
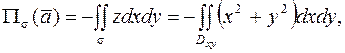
где 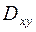 – проекция
– проекция 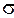 на
на  имеет форму круга с границей
имеет форму круга с границей 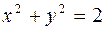 . Поэтому, переходя к полярным координатам, получим
. Поэтому, переходя к полярным координатам, получим
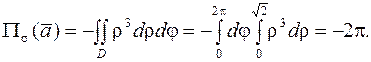
4 ФОРМУЛА ОСТРОГРАДСКОГО.
ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
Если функции  дифференцируемы в замкнутой области
дифференцируемы в замкнутой области 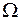 , ограниченной кусочно-гладкой поверхностью
, ограниченной кусочно-гладкой поверхностью  , то имеет место формула Остроградского
, то имеет место формула Остроградского
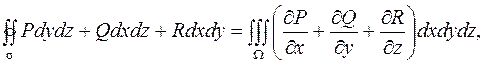 (8)
(8)
где выбрана внешняя сторона поверхности 
Дивергенцией векторного поля  в точке
в точке  называется предел отношения потока поля через замкнутую поверхность
называется предел отношения потока поля через замкнутую поверхность  , окружающую точку
, окружающую точку  к объему
к объему  тела, ограниченного этой поверхностью, при стремлении диаметра
тела, ограниченного этой поверхностью, при стремлении диаметра 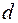 тела к нулю:
тела к нулю:
 .
.
По знаку дивергенции можно судить о наличии источника или стока векторного поля в точке  . Так, если
. Так, если  то в точке
то в точке  - источник, а если
- источник, а если 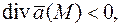 то сток. Если
то сток. Если 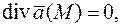 то в точке
то в точке  нет ни источника, ни стока. Абсолютная величина
нет ни источника, ни стока. Абсолютная величина  характеризует мощность источника или стока в точке
характеризует мощность источника или стока в точке  .
.
Для дифференцируемых  и
и 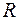 в области
в области 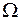 существует
существует
 (9)
(9)
в любой точке 
Тогда формула Остроградского в векторной форме имеет вид
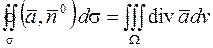 . (10)
. (10)
Векторное поле называется соленоидальным в области 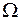 , если его дивергенция равна нулю в каждой точке области
, если его дивергенция равна нулю в каждой точке области 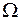 . Для соленоидального поля характерно, что в
. Для соленоидального поля характерно, что в 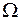 отсутствуют источники и стоки, а
отсутствуют источники и стоки, а 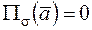 для любой замкнутой поверхности
для любой замкнутой поверхности  .
.
Задача 4.Вычислить поток векторного поля  через замкнутую поверхность, состоящую из частей
через замкнутую поверхность, состоящую из частей  и
и  в направлении внешней нормали (рисунок 3)
в направлении внешней нормали (рисунок 3)

Рисунок 3
Решение. Поле дифференцируемо во всем пространстве 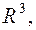 поэтому по формуле (9) получим
поэтому по формуле (9) получим

и по формуле (10)
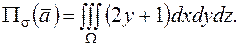
Интеграл удобно вычислять в цилиндрических координатах
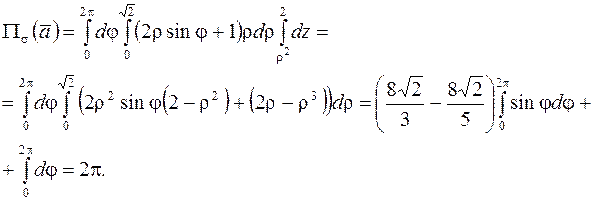
Замечание. Если поверхность  незамкнутая, то иногда использование формулы Остроградского в равенстве
незамкнутая, то иногда использование формулы Остроградского в равенстве

где  - еще одна поверхность, замыкающая область
- еще одна поверхность, замыкающая область 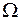 , может оказаться целесообразнее, чем вычисление поверхностного интеграла по поверхности
, может оказаться целесообразнее, чем вычисление поверхностного интеграла по поверхности 
Задача 5. Вычислить поток вектора  через внешнюю сторону части сферы
через внешнюю сторону части сферы 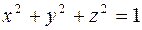 , которая вырезана конической поверхностью
, которая вырезана конической поверхностью  (рисунок 4).
(рисунок 4).
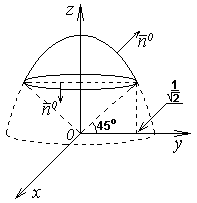 Рисунок 4
Рисунок 4
Решение. Линия пересечения сферы с конусом лежит в плоскости  поэтому дополним часть сферы еще этой плоскостью и получим замкнутую поверхность. Тогда поток через часть сферы
поэтому дополним часть сферы еще этой плоскостью и получим замкнутую поверхность. Тогда поток через часть сферы  будет получен интегралами (замечание)
будет получен интегралами (замечание)
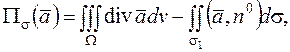
где  - нижняя сторона части плоскости
- нижняя сторона части плоскости  имеющая форму круга с границей
имеющая форму круга с границей 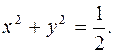 Вычислим
Вычислим



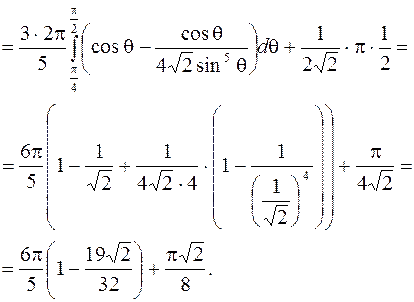
Здесь  - проекция круга из плоскости
- проекция круга из плоскости  на плоскость
на плоскость 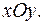
ЛИНЕЙНЫЙ ИНТЕГРАЛ
И ЦИРКУЛЯЦИЯ ВЕКТОРНОГО ПОЛЯ
Пусть в области 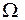 задано непрерывное векторное поле
задано непрерывное векторное поле  и ориентированная гладкая кривая
и ориентированная гладкая кривая  (с заданным направлением обхода). Обозначим единичный вектор касательной к линии
(с заданным направлением обхода). Обозначим единичный вектор касательной к линии 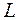 через
через  , направление которого совпадает с выбранным направлением на линии.
, направление которого совпадает с выбранным направлением на линии.
Линейным интегралом векторного поля  вдоль линии
вдоль линии  называется криволинейный интеграл первого рода от скалярного произведения векторов
называется криволинейный интеграл первого рода от скалярного произведения векторов  и
и  :
:
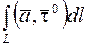 (11)
(11)
где  - дифференциал дуги кривой.
- дифференциал дуги кривой.
Если ввести в рассмотрение вектор  (
(  - радиус вектор точки, описывающей линию
- радиус вектор точки, описывающей линию  ) и обозначить его проекции на координатные оси
) и обозначить его проекции на координатные оси  , то формулу (11) можно записать в виде
, то формулу (11) можно записать в виде
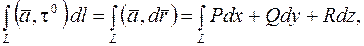 (12)
(12)
где вектор 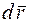 направлен по касательной к
направлен по касательной к  . Правая часть равенства (12) является криволинейным интегралом второго рода (криволинейный интеграл по координатам).
. Правая часть равенства (12) является криволинейным интегралом второго рода (криволинейный интеграл по координатам).
Если  -силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии
-силовое поле, то линейный интеграл равен работе, которую поле совершает по перемещению материальной точки вдоль ориентированной линии 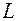 .
.
Для вычисления криволинейного интеграла второго рода, если кривая 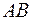 задана параметрическими уравнениями
задана параметрическими уравнениями  и при перемещении точки от
и при перемещении точки от 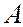 до
до  параметр меняется от
параметр меняется от  до
до 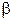 (выполнение условия
(выполнение условия 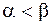 не обязательно), используется переход к определенному интегралу:
не обязательно), используется переход к определенному интегралу:
 (13)
(13)
Линейный интеграл называется циркуляцией векторного поля  , если
, если 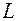 - замкнутая линия. Тогда из двух возможных направлений обхода контура
- замкнутая линия. Тогда из двух возможных направлений обхода контура  условимся называть положительным то, при котором область, лежащая внутри плоского контура остается слева по отношению к точке, совершающей обход (рисунок 5)
условимся называть положительным то, при котором область, лежащая внутри плоского контура остается слева по отношению к точке, совершающей обход (рисунок 5)
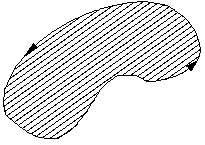
Рисунок 5
Если  - замкнутая пространственная кривая, то ее направление обхода специально оговаривается.
- замкнутая пространственная кривая, то ее направление обхода специально оговаривается.
Задача 6.Вычислить циркуляцию поля вектора  по замкнутой линии
по замкнутой линии  , состоящей из одного витка винтовой линии
, состоящей из одного витка винтовой линии  от точки
от точки 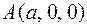 до точки
до точки  и прямолинейного отрезка
и прямолинейного отрезка  .
.
Решение. Виток 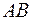 соответствует изменению параметра
соответствует изменению параметра  в уравнениях кривой от
в уравнениях кривой от  до
до  . Прямая
. Прямая  имеет направляющий вектор
имеет направляющий вектор 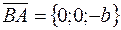 , поэтому ее параметрические уравнения будут
, поэтому ее параметрические уравнения будут  , где
, где  изменяется от
изменяется от  до
до  . Вычислим циркуляцию по формулам (12) и (13)
. Вычислим циркуляцию по формулам (12) и (13)
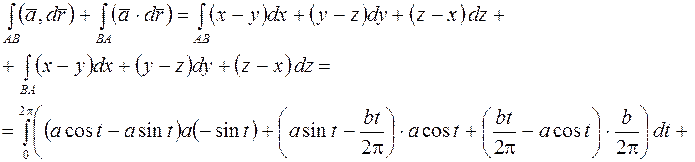

Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...