
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
График кармических структур человека
 Вот так, не спеша, мы и подошли к обсуждению кармических структур человека. Первый уровень организации человека – информационный. В материальном пространстве человек представлен на пяти уровнях (тело), со второго по шестой. Каждый из них формирует индивидуальную энергоинформационную структуру. И получается система тонких тел, которых, соответственно, тоже пять: эфирное, астральное, ментальное, каузальное и будхическое (рис. 1, 2). А дальше пошла Среда. Мы с вами рыбки, которые плавают в едином для всех океане. В материальном пространстве у нас единая на всех функция Сверхсознания – тонкие процессы в сумме создают среду на уровнях от минерального до общественного. Имеется еще и седьмой уровень, который находится вне человека – всеобъемлющий космический уровень, состоящий из всего, что существует.
Вот так, не спеша, мы и подошли к обсуждению кармических структур человека. Первый уровень организации человека – информационный. В материальном пространстве человек представлен на пяти уровнях (тело), со второго по шестой. Каждый из них формирует индивидуальную энергоинформационную структуру. И получается система тонких тел, которых, соответственно, тоже пять: эфирное, астральное, ментальное, каузальное и будхическое (рис. 1, 2). А дальше пошла Среда. Мы с вами рыбки, которые плавают в едином для всех океане. В материальном пространстве у нас единая на всех функция Сверхсознания – тонкие процессы в сумме создают среду на уровнях от минерального до общественного. Имеется еще и седьмой уровень, который находится вне человека – всеобъемлющий космический уровень, состоящий из всего, что существует.
Рис. 2. График кармических структур человека.
НМП – нематериальное пространство. МП – материальное пространство. Б – пространство БАРДО.
Все производится согласно Плану, состоящему из проектов всех уровней. Информационный уровень материального пространства связан с проектом информационного уровня в нематериальном пространстве. При этом постоянно идет взаимная сверка «проект-материализация». Зеркально в НМП также расположены тела человека – минеральный, клеточный, организменный, интеллектуальный, общественный. Со второго по шестой. Если здесь в МП у нас у всех индивидуальное Подсознание, а Сверхсознание у нас у всех одно, то в проектном НМП наоборот: у каждого из нас индивидуальное Сверхсознание, а Подсознание – тело – одно на всех. Таким образом, проекта индивидуального человека пока нет. Человек еще как человек не родился. Мы еще только идем к тому, чтобы появился Проект индивидуального человека.
Наша система предполагает реализацию Программы «минус один год», когда в процессе рождения будущего ребенка, сохраняющего свое сознание еще не рожденным, пойдет осознанная запись процессов зачатия и внутриутробного развития. То есть Ребенок сознательно проследит, как развивается его тело, и запишет эти процессы в памяти. После рождения, когда научится разговаривать, он поделится информацией со специалистами. И мы, наконец, все поймем про наши внутренние органы.
Программа подразумевает сохранение сознания после того, как физические тело уже отжило, и начался процесс реинкарнации, и внесение этого сознания в новое тело. Потом наступит следующий этап, когда тело менять уже будет не нужно, поскольку у человека возникнет позиция знания, и он сможет сохраняться в физическом теле бесконечно долго, управляя им. Физические возможности для этого имеются, неизвестен проект. Наш перспективный план заключается в познании, создании проекта индивидуального тела человека. Наша вторая ступень развивает внутреннее видение. А третья ступень дает возможность проектировать и переносить программы в материальное пространство, реализовывать их.
Вернемся к НМП. Там находятся проект плотного тела, проект тонких тел, проект среды и проект космоса – седьмого всеобъемлющего уровня. Предположим, что из пространства идей (БАРДО) у Создателя возникла мысль: «А не создать ли мне новую ячейку в космосе – КПСС?» И развернул Создатель Идею в программу (рис. 2). «Всеобъемлющий уровень, - говорит, - станет таким-то». И поделил Великий Проект на отдельные детали (поэтажный план). Решил, какая будет Среда, каким Человек. Еще раз все проверил и произвел полную запись всех информационных процессов. Тут-то и начался процесс творения, сопровождаемый постоянной сверкой великого плана проекта с материальной реализацией космоса. И пошел процесс перетекания энергии информации от проекта космического пространства к его реализации. А при обратной сверке полученные сведения о реализации проходили сквозь все структуры до первоначального проекта. Так и появились два мощных энергоинформационных потока, которые проходят и через каждого из нас, – КундалинииАнтикундалини.
Чем занимаемся мы? На четвертом уровне ловим оба проходящих через нас потока. А нам говорят, что надо развивать тонкие тела, надо идти к Богу. Почему-то считается, что Бог располагается на уровне космоса в материальном пространстве. Да, это горизонтальный процесс развития инструментария. Это руки Бога, которые материализуют план. Идти нужно и в нематериальное пространство, развивая эффект присутствия. Мы самую малость осознаем себя на организменном уровне. Представьте себе, какой спектр влияния на нас находится за рамками нашего осознания.
Наша система предполагает развитие сверхчувственного восприятия, с помощью которого мы сможем удовлетворить любопытство и в НМП, и в МП. Согласно предлагаемой нами программе изучения тонкоматериального мира, мы изучаем, где находятся природные тонкоматериальные сущности, какие они и как влияют на человека. Начиная процесс познания с организменного уровня МП, мы отрабатываем алгоритм этого познания и далее используем его на всех прочих уровнях. Стал доступен клеточный уровень – применили алгоритм и рассмотрели. Стал доступен просто взгляд в НМП, на тот же организменный уровень – применили алгоритм и открыли для себя потрясающий мир и возможности. Совершенствуя алгоритм, мы начинаем расширять эффект своего присутствия. Это наш путь развития, в котором нет никакой мистики, а есть колоссальный труд и интерес. Следуя этому пути, мы можем воспитать детей уже по-другому, закладывая в них новые знания, традиции и обряды, предоставляя новые возможности в образовании, обучая умению быть защищенными на всех уровнях. Сейчас мы знаем, что руки надо мыть, а потом будем знать, как правильно взаимодействовать друг с другом, как ребенка зачать правильно, чтобы не было патологии, как его воспитать, как сохранить здоровье в зрелом возрасте и т.д. Представляете, что будет, если несвоевременно расшевелить кундалини и антикундалини? Наши дорогие предки, которые первыми шли по этому пути, сгорали, погибали от инсультов, инфарктов, раковых заболеваний. Нам необходимо выйти на такой уровень развития, чтобы не возникали патологические процессы.
Помимо горизонтального, у нас имеется еще и вертикальный путь развития. Первооснова всех процессов, основополагающие идеи заложены в пространстве БАРДО. Сверху идут процессы, связанные с будущим, снизу – с прошлым. Именно в этом пространстве располагается программа предназначения каждого человека, развертки его судьбы. В НМП находится проект-Рок, в МП – Судьба (материализация проекта), а программа расположена в БАРДО. В НМП и МП располагаются процессы, связанные с физическим телом. За них отвечает горизонтальный компьютер. В НМП заложены программы роста, веса, силы, черт характера, качеств личности, которые необходимы для того, чтобы включились правильно процессы профессионального предназначения. НМП и МП – это две взаимодополняющие системы. Они подобны друг другу, они предназначены друг для друга. Если здесь в НМП все идет правильно, то и МП будет работать. Если в нас развивают тело и физические качества под один процесс, а мы пытаемся при этом идти другим путем (у человека есть свобода выбора), то можно все поломать, нарушить взаимодействие. В жизни начинаются катаклизмы – структуры пытаются вернуть человека на путь реализации предназначения.
С одной стороны, все очень сложно устроено. С другой стороны, у нас очень много сопровождающих механизмов, объектов, можно сказать, ангелов-хранителей. Мы даже представить себе не можем, как пытаются руки, которые делают этот мир, поставить нас на то место, где мы должны стоять. Как только человек встает на свое место, происходит трансформация. Он перестает болеть, прекращаются проблемы, наступает благополучие. Деталь встала на место, и система небо-человек-земля заработала.
А если человек еще начинает видеть и слышать, и слушать при этом свое сердце! Тот, кто знаком с христианскими техниками, христианством и последователями истихазма, могут вспомнить, например, такое выражение: нужно отпустить ум, сердце, отключить ум и начинать слушать свое сердце, и жить только этим. На первой ступени мы учимся отключать свою голову и слушать свои ощущения, и через некоторое время мы с удивлением замечаем, что наши руки где-то идут быстрее, где-то останавливаются, где-то появляется желание более активного движения. Мы начинаем принимать решения сердцем, не анализируя мозгами. Хотим мы этого или не хотим, наш ум автоматически погружается в сердце. И руки начинают слушать именно сердце. Для этого не надо молиться – мы просто оставили все свои заботы где-то там за дверью и начали слушать себя и друг друга. Система включилась, и через некоторое время, благодаря тому, что мозги отключены, начинает резонировать перикард, воспринимая истинную информацию напрямую. Через некоторое время можно очень хорошо включить экран внутреннего видения. Как только вы научились отключать свое сознание, научились доверять своей СС функции, доверять своему сердцу, пошел этот процесс.
Все наши упражнения первой ступени перекликаются с древними технологиями, которые использовались и используются до сих пор в любой религиозной практике (шаманизме, буддизме, даосизме, иудаизме, православии). Технологии эти являются истинными и базовыми, и человек не может двигаться в своем развитии, не используя их. Заслуга В.М. Бронникова в том, что он смог выделить алгоритм упражнений, которые не ориентированы на религиозные практики, мистические и эзотерические вещи, а построены на знании физиологии человека и трех функциональных систем С, ПС и СС. Поэтому эффект достигается быстро и просто.
Как и любая другая эффективная методика, наша система опасна в руках безграмотного и безответственного человека. Тем не менее, она относится к одной из наиболее безопасных систем, когда знаешь, как ее использовать, и насколько серьезные процессы стоят за любыми техниками. Да, это опасно, так же, как нож опасен в руках безграмотного непрофессионального хирурга. Точно так же, как опасны любые техники, применяемые неграмотным психологом. Обладая знанием и ответственностью, мы должны быть осторожны по отношению к себе и окружающим. Наша система относится к ликбезу. Мы просто даем вам информацию. Вы ее узнали, значит, что-то подскажет вам, как поступить дальше в этой жизни, как помочь себе и своим близким прожить еще много лет счастливой здоровой жизнью.
Взаимодействие Рока (НМП) и Судьбы (МП) является Кармой. Меняя свой проект, мы меняем свою судьбу. Такой наглядный пример, результат применения нашего метода. Все вы знаете о Саше Левите. С ним мы были в Иркутске, в реабилитационном центре, где работают с детишками со сложными патологиями. Мануальный терапевт центра занимается также диагностикой состояния здоровья по ушной раковине и по ладоням. Он посмотрел на Сашины ладони и был немало изумлен. Оказалось, что на одной руке у Саши проектировался очень низкий уровень развития, а на другой ладони отображены уникальные способности, новая судьба. Это говорит о том, что Саша смог проект-рок, который у него был изначально, переделать и создать себе новую судьбу. Человек способен изменить свою судьбу, если он этого хочет. Волшебных палочек нет, каждый решает сам. Мы только лотерейный билет вытягиваем, когда встречаемся с такой возможностью.
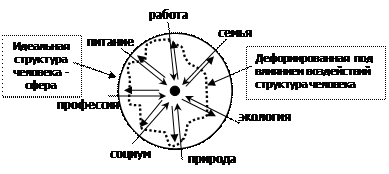
Рис. 3. Схема взаимовлияний человека и среды.
Можно рассмотреть это на следующей схеме (рис. 3). Человек – всего лишь точка в центре круга, а окружность – это бесконечное множество влияющих на человека событий в среде, в которой он живет. Все согласятся, что бывают семьи благополучные, где все понимают и поддерживают друг друга, а бывают семьи с очень сложными взаимоотношениями. Бывает работа любимая, и бывает ненавидимая всеми фибрами души. Бывают продукты свежие, а бывают и не очень. Что ни возьми – погоду, солнце, луну, звезды – все влияет на человека (стрелки, направленные от окружности к точке). Ну а человек изо всех сил пытается противодействовать влияниям (стрелки из точки к окружности), уравновешивать их. В итоге каждый человек представляет собой деформированную структуру. Где те механизмы, защитные силы, где вообще силы, чтобы сопротивляться?! А поэтому надо расширять эффект своего присутствия. Надо продавливать пространство. Надо развить такие защитные механизмы, которые позволят нам успеть убежать от молнии, достойно ответить начальнику, гармонизировать семью, воспитать детей. Силы, которые можно использовать для решения всех этих задач, мы начинаем открывать в себе уже на первой ступени.
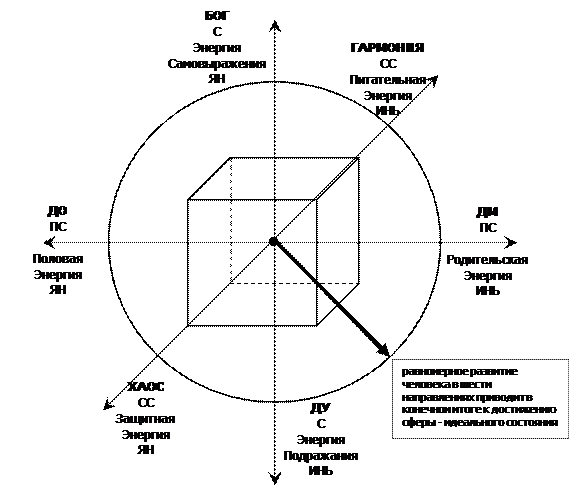 1.3. График реализации или развития любой идеи –
1.3. График реализации или развития любой идеи –
Кубический график развития
Рис. 4. График реализации или развития любой идеи – кубический график развития.
ДО – Духовный Отец. ДМ – Духовная Мать. ДУ – Духовный Учитель. ПС – Подсознание. С – Сознание. СС – Сверхсознание.
Кубический график (рис. 4) известен под разными именами с древних времен. Откройте даосские древние знания, и вы увидите данный график – знак Дао. Куб – это гармоничная, стабильная структура, которая развивается во всех направлениях одинаково. В центре куба находится точка – идея. Берем идею человека. Как он будет развиваться? А будет он развиваться согласно десяти базовым законам Космоса. Из них шесть относятся к развитию шести базовых энергий, которые формируют уже знакомые нам три функциональные системы.
Кубик развернут лицом к нам. Правая и левая грани отвечают за развитие функции Подсознания. Справа находится Духовный Отец – закон свободы действия, проявление янской энергии, половой. Здесь не имеются в виду половые отношения. Половая энергия на всех уровнях – это наше проявление в социуме в виде какого-то действия. Слева находится Духовная Мать – тормоза, родительская энергия, иньский процесс, принятие энергии и информации. У человека развитого должно быть три круга развития. Мы с вами (современные, неразвитые люди) проживаем только первый круг развития. Половая и родительская базовые энергии созревают в течение этого первого круга трижды (рис. 5). В возрасте 16-25 лет, когда ребенок перешел во взрослое состояние, функциональная система ПС созревает впервые. Как это проявляется в жизни? Человек женится и рождает ребенка. Половая и родительская энергии – это самая слабая пара энергий. Для того чтобы она полноценно сформировалась, организм предпринимает еще две попытки созревания: в 30-45 и в 50-70 лет.

Рис. 5. Слева – График созревания функциональной системы подсознания (ПС) – половой (ЯН) и родительской (ИНЬ) энергий – в первом круге развития человека. Справа – схема информационного развития человека: I – первый информационный круг развития человека, осознание кода. II – второй информационный круг развития человека, осознанный код действия. III – третий информационный круг развития функции ПС, осознанный код действия с реконструкцией.
В 30-45 лет мы уже начитались литературы, много чего узнали, и собираемся родить второго ребенка, но рожать-воспитывать уже по-другому, «по-умному», вложить в него все то, что прочитали. Первый (16-25) ребенок дублирует свойства родителей, получает то, что передается по роду. Второй ребенок (30-45) рождается с теми же генетическими качествами, но воспитывается по-другому. Его сознание будет уже другим, но генетически вложенные свойства не закрепятся.
В 50-70 лет созревание половой и родительской энергий происходит в третий раз. В это время уже созревают те качества, которые человек в жизни наработал. И эти качества уже закрепляются генетически. До 70 лет идет первый информационный круг развития, осознание кода (рис.5). Человек познает себя от рождения до созревания всех шести базовых энергий. Дальше происходит процесс «вылупления из яйца» и наступает следующий этап (еще 70 лет) – второй круг развития – осознанный код действия. То есть человек родился, закончил институт, и молодым специалистом пришел в жизнь. Во время второго круга развития точно так же, как во время первого, созревают 6 базовых энергий. После этого приходит третий круг развития, еще 70 лет – осознанный код действия с реконструкцией. То есть человек уже молодым специалистом побыл, наработал опыт, и имеет свое мнение. Появляется позиция хозяина и творца, который в этом мире наконец-то что-то веское скажет, построит и перестроит. Это уже позиция человека-Бога.
Следующая пара энергий относится к функции Сознания. Внизу – грань Духовного Учителя, закон памяти, энергия подражания, процесс инь. Это – впитывание энергии информации, это база, на которой мы стоим, это память, наработки всех поколений, живших до нас, это все знания, которые уже есть. Наверху находится грань вашего личного Бога или вашей личной цели. Энергия самовыражения. Функция сознания Ян. Выделение энергии информации. Функция сознания созревает в первый раз в 30-45 лет. Человек уже сформировался как личность, понимает свои цели. В этот период, уже имея много знаний и опыта, навязывает их окружающим, воспитывает всех вокруг, и, естественно, ребенка. В 50-70 лет функция сознания созревает повторно. Человек дополнительно учится, но и начинает передавать знания.
В 50-70 лет начинает созревать третья, самая мощная пара базовых энергий, относящаяся к сверхсознательной функции. Передняя грань относится к Хаосу, янский процесс, защитная энергия. Задняя грань – иньский процесс, Гармония, питательная энергия. Имеется в виду не только пища, но и получение энергии информации на всех уровнях. Мир хаотичен. Пропуская мир через себя, мы оставляем за спиной свою собственную гармонию. Приготовили пищу, убрались, с кем-то поговорили, кого-то полечили. Мы гармонизируем мир под себя. Ночью же, когда мы спим, мы обращены в мир гармонии, идет процесс гармонизации себя.
Почему генетически закрепляются наработки, полученные человеком в процессе жизни, у ребенка, рожденного родителями в 50-70 лет? Потому что в это время включается функция Сверхсознания, которая находится в проектном пространстве. Именно туда закладываются все те наработки, приобретенные в процессе жизни. Ребенок, рожденный в зрелом возрасте, отличается своими качествами от ребенка, рожденного в молодости. Считается, что поздние дети у зрелых родителей часто рождаются гениальными – работает Сверхсознание. А если у человека все правильно развивается, то первый круг развития завершается уже к 54 годам. Мы берем возраст 70 лет с поправкой на существующее сегодня хаотическое развитие. Созревание у многих современных людей даже и не наступает.
Итак, идея развивается в шести направлениях. Схематически – это точка в центре куба, каждая грань которого отражает свой процесс, и процессы эти происходят не одновременно. Все время идут колебания, чередования иньских и янских процессов – мы плаваем вокруг точки. Например, основной процесс у тех, кто пришел заниматься к нам – это смещение к учителю, то есть идет процесс ученичества. Человека пытаются наставить на путь истинный, ведущий к Богу. Это подразумевает равномерное развитие в шести направлениях и достижение в конечном итоге сферы. То есть из кубика необходимо превратиться в сферу. А сфера – это область Всевышнего, идеальная гармоничная система. Мы деформированы под процессы, которые нас окружают. Если бы мы жили вне гравитационных сил, то имели бы форму шара. Это идеальная структура. Наша задача – стать такими, какими нас задумали, что мы и реализуем через развитие в шести направлениях.
Кубический график можно применять в реальной жизни в оценке имеющейся идеи, оценке ее развития, оценке продвижения идеи к идеальному проекту. Возможности такого применения графика дают уже занятия по первой ступени.
Немного о действующих силах и букете энергий. Шесть базовых энергий – это статические закономерности. В динамике они создают букет из 24 действующих сил на каждом уровне (рис. 6). Откуда берется энергия, которая генерируется каждым человеком? Возникает она, когда срабатывает разность потенциалов между прошлым, настоящим и будущим. Мы были ребенком (прошлое). Сейчас мы зрелые люди (настоящее). Впереди – долгие годы жизни (будущее). Клетка, молекулы, органы были в прошлом, есть в настоящем, будут в будущем. И функционирование их в детстве, в зрелом возрасте и в старости отличается. Это выражается в напряженности или проявлении действующих сил. Есть некое пространство, где человек существует одновременно в прошлом, настоящем и будущем.
Для прошлого можно нарисовать кубик в виде круга событий (рис. 6). Точка-идея в центре и шесть базовых энергий: две энергии функции Подсознания (от круга к точке идет иньская энергия, от точки к кругу – янская); две энергии функции Сознания; две энергии функции Сверхсознания. Одновременно идет дыхание всех систем, сжатие и расширение, скручивание и раскручивание, процессы от точки к кругу и наоборот. Это еще две энергии – центробежная и центростремительная. Итого восемь действующих сил в срезе прошлого. В срезе будущего находятся такие же восемь действующих сил. И в настоящем – тоже восемь.
Между двумя энергиями Подсознания прошлого и двумя энергиями Подсознания будущего возникает разница потенциалов, и идет движение от прошлого к будущему (янский процесс) и от будущего к прошлому (иньский процесс). Каждая пара энергий имеет разное качество в прошлом и будущем. Вспомните кундалини и антикундалини, напряжение между космосом в проекте и космосом в материализации. Весь букет энергий
 проходит сквозь нас. Но букеты энергий, проходящие через каждого из нас, разные, так как все мы по-разному развиваемся (мужчина, женщина, разная биохимия, разные деформации в процессе жизни и так далее). Восемь плюс восемь плюс восемь составляют букет из двадцати четырех действующих сил, которые между собой взаимодействуют.
проходит сквозь нас. Но букеты энергий, проходящие через каждого из нас, разные, так как все мы по-разному развиваемся (мужчина, женщина, разная биохимия, разные деформации в процессе жизни и так далее). Восемь плюс восемь плюс восемь составляют букет из двадцати четырех действующих сил, которые между собой взаимодействуют.
Если через человека идут слабые потоки космической и солнечной энергий, а рядом находится сильный человек, то между ними возникает напряженность – родительской энергии с родительской, половой с половой и так далее, то есть букеты их энергий начинают взаимодействовать. И чем больше разница потенциалов, тем мощнее будет воздействие друг на друга. Поэтому в нашей системе необходимо взаимодействовать с людьми, с которыми у вас очень сильно отличается энергетика. С проблемными детьми, с больными. Если у вас нет такой же патологии (не по диагнозу, а по смыслу), то вам с таким человеком выгодно работать. Потому что в нем работает такой букет энергий, который в вас не работает. А в нем не работают, не развиты, закрыты, нормально не проявляются те букеты энергий, которые хорошо работают у вас. Вы, взаимодействуя друг с другом, раскрываете и активизируете именно эти нераскрытые энергии.
Поэтому работа в группе эффективнее, чем индивидуальные занятия. Чем группа больше и чем чаще идет смена партнера, тем быстрее достигается наилучшее раскрытие, тем выше уровень развития. По отношению друг к другу мы работаем как мощные стартеры, мы раскручиваем, заводим, возбуждаем организм, который дальше начинает работать в хорошем активном режиме. Нужно только помочь запустить. На это уходит порядка десяти занятий. Полезно посещать клубные мероприятия, работая в группе и организуя, таким образом, энергетические всплески для своего организма. В дальнейшем мы будем говорить о том, как какие упражнения воздействуют на наш организм в целом и на отдельные его системы, структуры. И как все это влияет на развитие головного мозга.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...