Верхний и нижний пределы последовательности.

Всякая ограниченная последовательность имеет хотя бы одну предельную точку.

Определение. Наибольшая (наименьшая) из предельных точек ограниченной последовательности {x_n} наз. ёе верхним (нижним) пределом и обозначается: .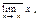

Если последовательность {x_n} сходится, то она имеет ровно одну предельную точку (ее предел), и в этом случае = = .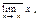

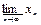Если ограниченная последовательность имеет конечное число предельных точек, то среди них, очевидно, есть наибольшая и наименьшая, то есть в этом случае последовательность имеет верхний и нижний пределы. Если же число предельных точек бесконечно, то существование верхнего и нижнего пределов не является очевидным.

Теорема 6.3. Любая ограниченная последовательность имеет верхний и нижний пределы.

Доказательство: Пусть {x_n} - ограниченная поледовательность. Обозначим через {a} множество всех предельных точек этой последовательности. Так как это множество ограничено и непусто, то оно имеет точные грани. Обозначим = Sup {a}, 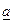= inf {a}.

Достаточно доказать, что 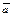Î {a}, 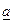Î {a}. Проведем доказательство для .

Рассмотрим произвольную e-окрестность точки и, кроме того, рассмотрим -окрестность точки .

По определению точной верхней грани, существует точка a Î {a}: a Î { 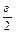-окрестности точки a}, а по определению 2 предельной точки в -окрестности точки a содержится бесконечно много членов последовательности {x_n}. Но { 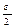-окрестность точки a} Ì {e-окрестности точки }, тем самым, в e-окрестности точки 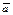содержится бесконечно много членов последовательности {x_n}, а это и означает, что - предельная точка последовательности {x_n}, то есть Î {a}.

БИЛЕТ 12

Числовая последовательность удовлетворяет условию Коши называется фундаментальной. Можно доказать, что и справедлива и обратное утверждение. Таким образом мы имеем критерий (необходимое и достаточное условие) сходимости последовательности.

В заключении рассмотрим вопрос критерия сходимости числовой последовательности.

Пусть т.е.: на ряду с натуральным числом 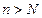можно подставить в последнее неравенство другое натуральное число 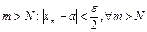,тогда

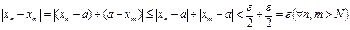
Мы получили следующее утверждение:

Если последовательность 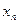сходится, выполняется условие Коши:

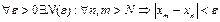(5)

Числовая последовательность удовлетворяет условию Коши называется фундаментальной. Можно доказать, что и справедлива и обратное утверждение. Таким образом мы имеем критерий (необходимое и достаточное условие) сходимости последовательности.

Критерий Коши.

Для того, чтобы последовательность имела предел необходимо и достаточно, что бы она была фундаментальной.

Второй смысл критерия Коши. Члены последовательност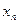и и 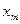где n и m – любые неограниченно сближающиеся при .

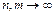БИЛЕТ 13

Односторонние пределы.

Определение 13.11. Число А называется пределом функции у = f(x) при х, стремящемся к х₀ слева (справа), если 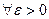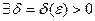такое, что |f(x)-A|<ε при x₀ – х < δ (х - х₀ < δ).

Обозначения: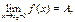

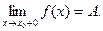
Теорема 13.1(второе определение предела). Функция y=f(x) имеет при х, стремящемся к х₀, предел, равный А, в том и только в том случае, если оба ее односторонних предела в этой точке существуют и равны А.

Доказательство.

1) Если 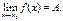, то и для x₀ – х < δ, и для х - х₀ < δ |f(x) - A|<ε, то есть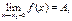

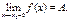
1) Если 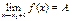, то существует δ₁: |f(x) - A| < ε при x₀ – x < δ₁ и δ₂: |f(x) - A| < ε при х - х₀ < δ₂. Выбрав из чисел δ₁ и δ₂ меньшее и приняв его за δ, получим, что при |x - x₀| < δ |f(x) - A| < ε, то есть 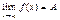. Теорема доказана.

Замечание. Поскольку доказана эквивалентность требований, содержащихся в определении предела 13.7 и условия существования и равенства односторонних пределов, это условие можно считать вторым определением предела.

Определение 4 (по Гейне)

Число А называется пределом функци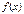и при 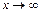если любой ББП 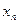значений аргумента последовательность 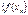соответствующих значений функции сходится к А.

Определение 4 (по Коши).

Число А называется 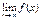если 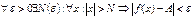. Доказывается, что эти определения равносильны.

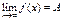
БИЛЕТ 14 и 15

Свойства предела ф-ции в точке

1) Если предел в т-ке сущ-ет, то он единственный

2) Если в тке х0 предел ф-ции f(x) lim(x®x0)f(x)=A

lim(x®x0)g(x)£B=> то тогда в этой т-ке $ предел суммы, разности, произведения и частного. Отделение этих 2-х ф-ций.

а) lim(x®x0)(f(x)±g(x))=A±B

б) lim(x®x0)(f(x)*g(x))=A*B

в) lim(x®x0)(f(x):g(x))=A/B

г) lim(x®x0)C=C

д) lim(x®x0)C*f(x)=C*A