Правило квантования круговых орбит.

В рамках формализма Бора в основу решения проблемы заложено общее выражение для полной энергии электрона в самом общем виде:

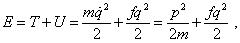(1)

где в данном конкретном случае q - обобщённая координата точечного электрона на орбите, рассматриваемого как линейный осциллятор, p - его импульс, Т, U - соответственно его кинетическая и потенциальная энергии. В качестве второго моделирующего уравнения используется постулат для отбора квантовых орбит, который является обобщением постулата Планка и который использовался Бором в его базовой работе "О строении атомов и молекул". “Согласно этому последнему постулату из всех возможных состояний линейного осциллятора осуществляются только такие, энергия которых равна

(2)

Путём стандартных преобразований и замены

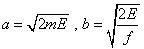(3)

Шпольский приводит (1) к каноническому виду эллипса

(4)

и далее вычисляет площадь данной геометрической фигуры, получая в результате

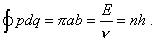(5)

Далее Шпольский переходит от обобщённых координат к координатам, описывающим орбитальное движение электрона, беря в качестве такой координаты полярный угол , характеризующий положение электрона на круговой орбите. При этом

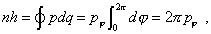(6)

откуда

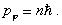(7)

Последняя величина является, таким образом, квантовой единицей момента количества движения.

Элементарная Боровская теория водородного атома.

Бор предположил, что из всех возможных орбит электрона осуществляются только те. для которых мо­мент импульса равен целому кратному постоянной План­ка h, деленной на 2л:

m_evr = nh (п — 1, 2, 3, ...).(1) Число п называется главным к в а н т о в ы м ч и с л о м.

Рассмотрим электрон, движущийся в поле атомного ядра с зарядом Ze. При Z = 1 такая система соответ­ствует атому водорода, при иных Z — водородоподоб­ному иону. Согласно второму закону Ньютона произведение массы электро­на т_е на его центростремительное ускорение v²/r дол­жно равняться кулоновской силе: т_е *( υ ²/r)= Ze^2/r^2 (2)

Исключая υ из (1) и (2), получаем, что радиус электронных орбит в атоме может принимать лишь ряд дискретных значений: rn=(h^2*n^2)/(me*Z*e^2) (n= 1, 2, 3, ...). (3)

Для первой орбиты водородного атома (Z = 1, п = 1) получается r1= h^2/(me*e^2)= 0,529 А, (4)

т, е. величина порядка газокинетических размеров атома.

Внутренняя энергия атома слагается из кинетической энергии электрона (ядро неподвижно) и энергии взаи­модействия электрона с ядром (потенциальной энергии): E=(me*υ^2)/2 – (Z*e^2)/r

Из (2) следует, что (me*υ^2)/2 = (Z*e^2)/2r, Следовательно, E=(Z*e^2)/2r - (Z*e^2)/r = - (Z*e^2)/2r

Наконец, учтя значения г, даваемые (3), получим дозволенные значения внутренней энергии атома:

En= - [(me*e^4)/2h^2]*[Z^2/n^2] (n = 1, 2, 3, ...). (5)

При переходе атома водорода (Z = 1) из состояния п в состояние т испускает­ся квант

Hω=- [(me*e^4)/2h^2]*[1/n^2 – 1/ m^2]

Частота испущенного света равна

ω= [(me*e^4)/2h^3]*[1/m^2 – 1/ n^2]

Таким образом, мы пришли к обоб­щенной формуле Бальмера, при чем для постоянной Ридберга получает­ся значение:

R =(me*e^4)/2h^3 (6)

Если подставить в это выражение значения входящих в него констант, получается величина, хорошо согласующая с экспериментальным значением постоянной Ридберга.

Гипотеза де – Бройля.

В 1924 г. Луи де Бройль выдвинул гипотезу, что дуализм не является особенностью только оптических явлений, а имеет универсальный характер. Частицы вещества также обладают волновыми свойствами. Если фотон обладает энергией и импульсом, то и частица (например электрон), движущаяся с некоторой скоростью, обладает волновыми свойствами, т.е. движение частицы можно рассматривать как движение волны.

Согласно квантовой механике, свободное движение частицы с массой m и импульсом (где υ – скорость частицы) можно представить как плоскую монохроматическую волну (волну де Бройля) с длиной волны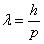

распространяющуюся в том же направлении (например в направлении оси х), в котором движется частица.

Зависимость волновой функции от координаты х даётся формулой

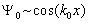, где 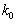– волновое число, а волновой вектор 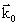направлен в сторону распространения волны или вдоль движения частицы: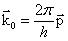

Таким образом, волновой вектор монохроматической волны, связанной со свободно движущейся микрочастицей, пропорционален её импульсу или обратно пропорционален длине волны.

Поскольку кинетическая энергия сравнительно медленно движущейся частицы 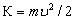, то длину волны можно выразить и через энергию:

При взаимодействии частицы с некоторым объектом – с кристаллом, молекулой и т.п. – её энергия меняется: к ней добавляется потенциальная энергия этого взаимодействия, что приводит к изменению движения частицы. Соответственно, меняется характер распространения связанной с частицей волны, причём это происходит согласно принципам, общим для всех волновых явлений. Поэтому основные геометрические закономерности дифракции частиц ничем не отличаются от закономерностей дифракции любых волн. Общим условием дифракции волн любой природы является соизмеримость длины падающей волны λ с расстоянием d между рассеивающими центрами:

21. Принцип неопределенности. По соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определен­ную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, p_у, p_z), причем неопределенности этих величин удовлетворяют условиям

, ,

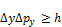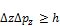
т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.

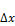, –ширина щели, – длина волны

При движении по траектории в любой момент времени с определенными значениями координат и скорости, соотношение неопределенностей:

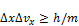
Cоотношение неопределенностей для энергии Е и времени t:
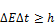DЕ — неопределенность энергии некоторого состояния системы, Dt — промежуток времени, в течение которого оно существует. Следовательно, систе­ма, имеющая среднее время жизни Dt, не может быть охарактеризована определенным значением энергии; разброс энергии DE=h/Dt возрастает с уменьшением среднего времени жизни.=>частота излученного фотона также должна иметь неопределенность Dn = DE/h, т. е. линии спектра должны характеризо­ваться частотой, равной n± DE/h.

Уравнение шредингера

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шредин­гера имеет вид

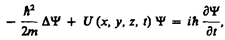(217.1)

где ћ=h/(2p), т—масса частицы, D—оператор Лапласа i — мнимая единица, U (х, у, z, t) — потенциальная функция частицы в силовом поле, в котором она движется, Y(х, у, z, t) — искомая волновая функция частицы.

Уравнение справедливо для любой частицы (со спином, равным 0), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью v<<с. Оно дополняется условиями, накладываемыми на волновую функцию:

1) волно­вая функция должна быть конечной, однозначной и непрерывной

2) производные должны быть непрерывны;

3) функция |Y|² должна быть интегрируема; это условие в простейших случаях сводится к условию нормировки вероятностей

Смысл пси-функции

При создании квантовой механики возникли новые принципиальные проблемы, в частности проблема физической природы волн де Бройля. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсив­ности волн де Бройля. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц, т. е. интенсивность волн де Бройля в данной точке пространства определяет число частил, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц является проявлением статистичес­кой (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

Чтобы устранить эти трудности, немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая Y(х, у, z, t). Эту величину называют также волновой функцией (или Y-функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

(216.1)

(|Y|²=YY*, Y* — функция, комплексно сопряженная с Y). Таким образом, описание состояния микрообъекта с помощью волновой функции имеетстатистический, вероят­ностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент време­ни t в области с координатами х и x+dx, у и y+dy, z и z+dz.

Квантование энергии

Некоторые физические величины, относящиеся к микрообъектам, изменяются не непрерывно, а скачкообразно. О величинах, которые могут принимать только вполне определенные, то есть дискретные значения (латинское "дискретус" означает разделенный, прерывистый), говорят, что они квантуются.

В 1900 г. немецкий физик М. Планк, изучавший тепловое излучение твердых тел, пришел к выводу, что электромагнитное излучение испускается в виде отдельных порций - квантов - энергии. Значение одного кванта энергии равно

ΔE = hν,

где ΔE - энергия кванта, Дж; ν - частота, с^-1; h - постоянная Планка (одна из фундаментальных постоянных природы), равная 6,626·10⁻³⁴ Дж·с.
Кванты энергии впоследствии назвали фотонами.

Идея о квантовании энергии позволила объяснить происхождение линейчатых атомных спектров, состоящих из набора линий, объединенных в серии.

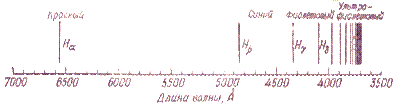
Еще в 1885 г. швейцарский физик и математик И.Я. Бальмер установил, что длины волн, соответствующие определенным линиям в спектре атомов водорода, можно выразить как ряд целых чисел. Предложенное им уравнение, позднее модифицированное шведским физиком Ю.Р. Ридбергом, имеет вид:

1 / λ = R(1 / n₁² − 1 / n₂²),

где λ - длина волны, см; R - постоянная Ридберга для атома водорода, равная 1,097373·10⁵ см⁻¹, n₁ и n₂ - целые числа, причем n₁ < n₂.

Квантование момента импульса

Момент импульса М является одной из важнейших характеристик движения. Его значение связано с тем, что М сохраняется, если система изолирована или движет­ся в центральном силовом поле. Однако в квантовой теории мо­мент импульса существенно отличается от классического. А именно, модуль момента импульса может быть задан сколь угодно точно только с одной из проекций, например, М_z. Дру­гие две проекции оказываются полностью неопределенными.

Это означает, что направление момента М в пространстве является неопределенным. Наглядно подобную ситуацию можно попы­таться представить так: вектор М как-то ♦ размазан» по образующим конуса, ось кото­рого совпадает с направлением координатной оси Z (рис. 5.1). В этом случае вполне опреде­ленное значение имеет лишь проекция М_г. Другие две проекции, М_х и М_у, оказываются полностью неопределенными.

Принцип суперпозиции

Рассмотрим метод определения модуля и направления вектора напряженности Е в каж­дой точке электростатического поля, создаваемого системой неподвижных зарядов Q₁, Q₂, ..., Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механике принцип независимости действия сил, т. е. результирующая сила F, дейст­вующая со стороны поля на пробный заряд Q₀, равна векторной сумме сил F_i, приложенных к нему со стороны каждого из зарядов Q_i:

(80.1)

Согласно (79.1), F= Q₀E и F_i = Q₀Е_i, где Е—напряженность результирующего поля, а Е_i — напряженность поля, создаваемого зарядом Q_i. Подставляя последние выраже­ния в (80.1), получаем

(80.2)

Формула (80.2) выражаетпринцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Принцип суперпозиции применим для расчета электростатического поля элект­рического диполя.

27) Прохождение частиц через потенциальный барьер.

Туннельный эффект

Рис. 1.7. Потенциальный барьер конечной ширины

Рассмотрим поведение квантово-механической частицы при прохождении через потенциальный барьер конечной ширины (рис.1.7). Ограничимся рассмотрением одномерной задачи, когда ось x параллельна движению частицы. В каждой из трех областей I, II и III потенциальная энергия микрочастицы постоянна, но при переходе из одной области в другую меняется скачком. Эта задача моделирует многие физически важные явления, например, выход электронов из металлов, распад атомных ядер и др.

Уравнение Шредингера в этом случае будет иметь вид

(1.40)

В области I уравнение (1.40) будет иметь вид

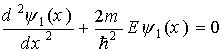(1.41)

Для области II уравнение Шредингера запишется в виде

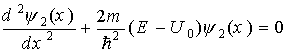. (1.45)

Уравнение Шредингера для микрочастицы в области III будет иметь тот же вид, что и в области I. Общее решение для этой области будет отличаться от решения (1.44) тем, что в области III нет отраженной волны (b₃ = 0)

. (1.48)

В случае потенциального барьера произвольной формы (рис. 1.8) проницаемость барьера выражается приближенной формулой

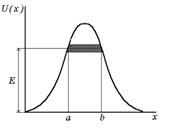Рис. 1.8. Потенциальный барьер произвольной формы

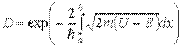, (1.53)

которая, как нетрудно увидеть, является обобщением формулы (1.52).

Таким образом, квантово-механической частице для преодоления потенциального барьера необязательно иметь энергию больше, чем высота барьера. Она как бы проходит через “туннель” (заштрихованная область на рис. 1.8), расположенном на высоте E, где E - полная энергия микрочастицы. В связи с этим рассмотренное явление называют туннельным эффектом.