
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Линейные неоднородные дифференциальные уравнения с постоянными
коэффициентами.
Уравнения с правой частью специального вида. Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения. Различают следующие случаи:
I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
где Тогда частное решение ищется в виде:
Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Пример. Решить уравнение Решим соответствующее однородное уравнение:
Теперь найдем частное решение исходного неоднородного уравнения. Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.
Частное решение ищем в виде: Т.е. Теперь определим неизвестные коэффициенты А и В. Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.
Итого, частное решение:
II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно. Тогда частное решение неоднородного уравнения будет иметь вид:
где число r показывает сколько раз число
Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию. Т.е. если уравнение имеет вид:
Для иллюстрации решим рассмотренный выше пример другим способом. Пример. Решить уравнение
Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (-sinx). Составим и решим характеристическое уравнение:
1. Для функции f1(x) решение ищем в виде Получаем:
Итого:
2. Для функции f2(x) решение ищем в виде: Анализируя функцию f2(x), получаем:
Таким образом,
Итого:
Т.е. искомое частное решение имеет вид:
Общее решение неоднородного дифференциального уравнения:
Рассмотрим примеры применения описанных методов.
Пример. Решить уравнение Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:
Общее решение однородного уравнения: Теперь найдем частное решение неоднородного уравнения в виде:
Воспользуемся методом неопределенных коэффициентов.
Подставляя в исходное уравнение, получаем:
Общее решение линейного неоднородного уравнения: Пример. Решить уравнение
Характеристическое уравнение: Общее решение однородного уравнения: Частное решение неоднородного уравнения:
Находим производные и подставляем их в исходное неоднородное уравнение:
Нормальные системы обыкновенных дифференциальных уравнений.
Определение. Совокупность соотношений вида:
где х- независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.
Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений. Такая система имеет вид:
Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.
Теорема. (Теорема Коши). Если в некоторой области (n-1) –мерного пространства функции системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х0 и удовлетворяющее начальным условиям
Определение. Общим решениемсистемы дифференциальных уравнений вида (1) будет совокупность функций
|
Последнее изменение этой страницы: 2016-06-09; просмотров: 15109
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...



 - многочлен степени m.
- многочлен степени m.

 .
.


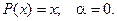


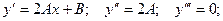


 Тогда общее решение линейного неоднородного дифференциального уравнения:
Тогда общее решение линейного неоднородного дифференциального уравнения:





 является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.
является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2. , то частное решение этого уравнения будет
, то частное решение этого уравнения будет  где у1 и у2 – частные решения вспомогательных уравнений
где у1 и у2 – частные решения вспомогательных уравнений и
и 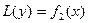


 .
. Т.е.
Т.е. 

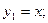
 .
.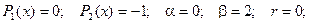



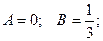
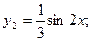










 Частное решение имеет вид:
Частное решение имеет вид: 



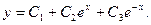




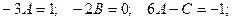

 Получаем общее решение неоднородного дифференциального уравнения:
Получаем общее решение неоднородного дифференциального уравнения:

 (1)
(1)
 …
…  непрерывны и имеют непрерывные частные производные по
непрерывны и имеют непрерывные частные производные по  , то для любой точки
, то для любой точки  этой области существует единственное решение
этой области существует единственное решение

 ,
,  , …
, …  , которые при подстановке в систему (1) обращают ее в тождество.
, которые при подстановке в систему (1) обращают ее в тождество.