
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Нормальные системы линейных однородных дифференциальных
уравнений с постоянными коэффициентами.
При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.
Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:
Решения системы (2) обладают следующими свойствами:
1) Если y, z, u – решения системы, то Cy, Cz, Cu , где C = const – тоже являются решениями этой системы. 2) Если y1, z1, u1 и y2, z2, u2 – решения системы, то y1 + y2, z1 + z2, u1 + u2 – тоже являются решениями системы.
Решения системы ищутся в виде: Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на ekx, получаем:
Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:
В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнениеми имеет три корня k1, k2, k3. Каждому из этих корней соответствует ненулевое решение системы (2):
Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):
Пример. Найти общее решение системы уравнений:
Составим характеристическое уравнение:
Решим систему уравнений:
Для k1: Полагая
Для k2:
Общее решение системы:
Этот пример может быть решен другим способом:
Продифференцируем первое уравнение: Подставим в это выражение производную у¢ =2x + 2y из второго уравнения.
Подставим сюда у, выраженное из первого уравнения:
Обозначив
Пример. Найти решение системы уравнений
Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменная х). Для решения продифференцируем первое уравнение по х. Получаем:
Заменяя значение z’ из второго уравнения получаем: С учетом первого уравнения, получаем: Решаем полученное дифференциальное уравнение второго порядка.
Общее решение однородного уравнения:
Теперь находим частное решение неоднородного дифференциального уравнения по формуле
Общее решение неоднородного уравнения:
Пример. Найти решение системы уравнений:
Составим характеристическое уравнение:
1) k = -1.
Если принять g = 1, то решения в этом случае получаем:
2) k2 = -2.
Если принять g = 1, то получаем:
3) k3 = 3.
Если принять g = 3, то получаем:
Элементы теории устойчивости.
Теория устойчивости решений дифференциальных уравнений является одним из разделов качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента. Этот метод особенно важен, т.к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т.е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически. Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:
и начальные условия: Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.
Теорема. (о непрерывной зависимости решения от начальных условий) Если правая часть дифференциального уравнения Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.
Определение. Если
справедливы неравенства
(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)
Т.е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при t ³ t0. Если Исследование на устойчивость по Ляпунову произвольного решения
Тогда:
Система (2) имеет тривиальное (равное нулю) решение
Теорема. Решение Это тривиальное решение называется положением равновесияили точкой покоя.
Определение. Точка покоя
следует
Теорема. (Теорема Ляпунова). Пусть задана система имеющая тривиальное решение Пусть существует дифференцируемая функция 1) 2) Полная производная функции v вдоль фазовой траектории (т.е. вдоль решения yi(t) системы (1)) удовлетворяет условию: Тогда точка покоя Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат где b - постоянная величина, то точка покоя Функция v называется функцией Ляпунова.
Классификация точек покоя.
Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами
Характеристическое уравнение этой системы имеет вид:
Рассмотрим следующие возможные случаи:
1) Корни характеристического уравнения действительные, отрицательные и различные.
Точка покоя
2) Корни характеристического уравнения действительны и
В этом случае точка покоя также будет устойчива.
3) Хотя бы один из корней В этом случае точка покоя
4) Оба корня характеристического уравнения положительны В этом случае точка покоя
Если полученного решения Возможны следующие случаи:
a a
Устойчивый узел. Неустойчивый узел. Седло. 5) Корни характеристического уравнения комплексные Если р = 0, т.е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову. Такая точка покоя называется центром. Если p< 0, то точка покоя устойчива и называется устойчивым фокусом. Если p > 0, то точка покоя неустойчива и называется неустойчивым фокусом.
Уравнения математической физики.
Уравнения в частных производных.
Определение. Дифференциальным уравнением в частных производныхназывается уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.
Порядкомдифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решениемуравнения будет некоторая функция
|
Последнее изменение этой страницы: 2016-06-09; просмотров: 789
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...
 (2)
(2)








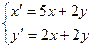




 (принимается любое значение), получаем:
(принимается любое значение), получаем: 

 Полагая
Полагая  (принимается любое значение), получаем:
(принимается любое значение), получаем: 
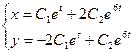









 , получаем решение системы:
, получаем решение системы: 

 .
.



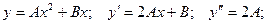



 Подставив полученное значение в первое уравнение системы, получаем:
Подставив полученное значение в первое уравнение системы, получаем:









 Общее решение имеет вид:
Общее решение имеет вид:
 (1)
(1)
 непрерывна и по переменной у имеет ограниченную частную производную
непрерывна и по переменной у имеет ограниченную частную производную  на области прямоугольника, ограниченного
на области прямоугольника, ограниченного  , то решение
, то решение  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  , непрерывно зависит от начальных данных, т.е. для любого
, непрерывно зависит от начальных данных, т.е. для любого  , при котором если
, при котором если то
то  при условии, что
при условии, что где
где
 - решение системы дифференциальных уравнений, то это решение называется устойчивым по Ляпунову, если для любого
- решение системы дифференциальных уравнений, то это решение называется устойчивым по Ляпунову, если для любого  , такое, что для любого решения
, такое, что для любого решения  той же системы, начальные условия которого удовлетворяют неравенствам
той же системы, начальные условия которого удовлетворяют неравенствам

 , то решение j(t) называется асимптотически устойчивым.
, то решение j(t) называется асимптотически устойчивым.

 (2)
(2)
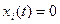 системы (2) устойчива по Ляпунову, если для любого
системы (2) устойчива по Ляпунову, если для любого 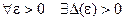 такое, что из неравенства
такое, что из неравенства
 .
. .
. , удовлетворяющая условиям:
, удовлетворяющая условиям: при
при 
 устойчива по Ляпунову.
устойчива по Ляпунову. выполнялось условие
выполнялось условие



 будет устойчива. Такая точка покоя называется устойчивым узлом.
будет устойчива. Такая точка покоя называется устойчивым узлом. или
или  .
. положителен.
положителен. .
. системы исключить параметр t, то полученная функция
системы исключить параметр t, то полученная функция  дает траекторию движения в системе координат XOY.
дает траекторию движения в системе координат XOY. b b
b b .
.
 , которая обращает уравнение в тождество.
, которая обращает уравнение в тождество.