
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
ПРИНЯТИЕ РЕШЕНИЙ ПОСЛЕ ПОСТРОЕНИЯ МОДЕЛИ
Не нам, господа, подражать Плинию.
Наше дело выравнивать линию.
К. Прутков
11.1. Интерпретация результатов
Адекватная линейная модель, которой мы теперь располагаем, имеет вид полинома первой степени. Коэффициенты полинома являются частными производными функции отклика по соответствующим переменным. Их геометрический смысл — тангенсы углов наклона гиперплоскости к соответствующей оси. Больший по абсолютной величине коэффициент соответствует большему углу наклона и, следовательно, более существенному изменению параметра оптимизации при изменении данного фактора.
До сих пор мы употребляли абстрактный математический язык. Перевод модели на язык экспериментатора называется интерпретацией модели.
Задача интерпретации весьма сложна. Ее решают в несколько этапов. Первый этап состоит в следующем. Устанавливается, в какой мере каждый из факторов влияет на параметр оптимизации. Величина коэффициента регрессии—количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О характере влияния факторов говорят знаки коэффициентов. Знак плюс свидетельствует о iом,-Что с увеличением значения фактора растет величина параметра оптимизации, а при знаке минус — убывает. Интерпретация знаков при оптимизации зависит от того, ищем ли мы максимум или минимум функции отклика. Если у ->. max, то увеличение значений всех факторов, коэффициенты которых имеют знак плюс, благоприятно, а имеющих знак минус — неблагоприятно. Если же у min, то, наоборот, благоприятно увеличение значений тех факторов, знаки коэффициентов которых отрицательны.
Далее выясняется, как расположить совокупность факторов в ряд по силе их влияния на параметр оптимизации. Факторы, коэффициенты которых незначимы, конечно не интерпретируются. Можно сказать только, что при данных интервалах варьирования и ошибке воспроизводимости они не оказывают существенного влияния на параметр оптимизации.
Изменение интервалов варьирования приводит к изменению коэффициентов регрессии. Абсолютные величины коэффициентов регрессии увеличиваются с увеличением интервалов. Инвариантными к изменению интервалов остаются знаки линейных коэффициентов регрессии. Однако и они изменятся на обратные, если при движении по градиенту (гл. 12) мы «проскочим» экстремум.
В некоторых задачах представляет интерес построение уравнения регрессии для натуральных значений факторов. Уравнение для натуральных переменных можно получить, используя формулу перехода (стр. 72). Коэффициенты регрессии изменятся. При этом пропадает возможность интерпретации влияния факторов но величинам и знакам коэффициентов регрессии. Вектор-столбцы натуральных значений переменных в матрице планирования ужо не будут ортогональными, коэффициенты определяются зависимо друг от друга. Если же поставлена задача получения интерполяционной формулы для натуральных переменных, такой прием допустим.
Пример 1. Определений оптимальных условий ионнообменного разделения вводима и празеодима (стр. 70) у -» шах.
Вспомним, что Si — концентрация промывающего раствора (элюанта), £г — рН этого же раствора, у — процентное содержание неодима в выходящем растворе — элюате.
После обработки эксперименаальных данных получено уравнение регрессии
$ = 88,0 — 2,0хх — 4,5Х2. «{6 } =0,30.
К увеличению параметра оптимизации приводит уменьшение значений факторов. Подставим в уравнение регрессии разные кодированные значения факторов и посмотрим, при каких значениях факторов увеличивается параметр оптимизации.
Если подставить в уравнение значения ^1=4-1 и ж2= +1, то получится
2/=88,0 - 2,0 (+1) - 4,5 (+1)=81,5.
Теперь подставим значения 1 и х2~—1
у=88,0 — 2,0 (-1) - 4,5 (—1)=94,5.
Уменьшение значений факторов действует благоприятно. Для увеличения параметра оптимизации нужно уменьшать значения факторов.
Запомните правило: если коэффициент регрессии отрицателен, то для увеличения параметра оптимизации надо уменьшать значение фактора, а если положителен, то увеличивать.
При минимизации параметра оптимизации можно изменить знаки коэффициентов (кроме Ь0) на обратные и поступать, как в первом случае.
Теперь мы получили основу для перехода к следующему этапу. Априорные сведения дают некоторые представления о характере действия факторов. Источниками таких сведений могут служить теория изучаемого процесса, опыт работы с аналогичными процессами или предварительные ошрты и т. д.
Если, например, ожидается, что с ростом температуры должно происходить увеличение параметра оптимизации, а коэффициент регрессии имеет знак минус, то возникает противоречие. Возможны две причины возникновения такой ситуации: либо в эксперименте допущена ошибка и он должен быть подвергнут ревизии, либо неверны априорные представления. Нужно иметь в виду, что эксперимент проводится в локальной области факторного пространства и коэффициент отражает влияние фактора только в этой области. Заранее не известно, в какой мере можпо распространить результат на другие области. Теоретические же представления имеют обычно более общий характер. Кроме того, априорная информация часто основывается на однофакторных зависимостях. При переходе к многофакторному пространству ситуация может изменяться. Поэтому мы должны быть уверены, что эксперимент проведен корректно. Тогда для преодоления противоречия можно выдвигать различные гипотезы и проверять их экспериментально. Эксперименты по проверке гипотез тоже можно планировать, но эти задачи здесь мы не рассматриваем.
В тех, довольно редких, случаях, когда имеется большая априорная информация, позволяющая выдвигать гипотезы о механизме явлений, можно перейти к следующему этапу интерпретации. Он сводится к проверке гипотез о механизме явлений и выдвижению новых гипотез.
Получение информации о механизме явлений не является обязательным в задачах оптимизации, но возможность такого рода следует использовать. Здесь особое внимание приходится уделять эффектам взаимодействия факторов. Как их интерпретировать?
Пусть в некоторой задаче взаимодействие двух факторов значимо и имеет положительный знак. Это свидетельствует о том, что одновременное увеличение, как и одновременное уменьшение, значений двух факторов приводит к увеличению параметра оптимизации (без учета линейных эффектов). А если эффект взаимодействия факторов Xj и х2 имеет отрицательный знак? Любая комбинация разных знаков хх и х2 приводит к росту параметра оптимизации.
Запомните правило: если эффект взаимодействия имеет положительный знак, то для увеличения параметра оптимизации требуется одновременное увеличение или уменьшение значений факторов, например сочетания: ^=+1 и x2 = ~j-l или жх=—1 и х2 =—1. Для уменьшения параметра оптимизации факторы должны одновременно изменяться в разных направлениях, например ^=+1 и х2 =—1 или хх~—1 и x2—~j-i.
Если эффект взаимодействия имеет отрицательный знак, то для увеличения параметра оптимизации факторы должны одновременно изменяться в разных направлениях, например
и х2 ——1 или хх=—1 и =-{-!.
13 Заказ Я> 588
Для уменьшения параметра оптимизации требуется одновременное увеличение или уменьшение факторов, т. е.
^=+1 и ж2=+1, или ху——1 и ж2=—1.
Вы видите, что интерпретация эффектов взаимодействия не так однозначна, как линейных эффектов. В каждом случае имеется два варианта. Какому из вариантов отдавать предпочтение? Прежде всего нужно учесть знаки линейных эффектов соответствующих факторов. Если эффект взаимодействия имеет знак плюс и соответствующие линейные эффекты отрицательны, то выбор однозначен: сочетание —1 и —1. Однако возможен случай, когда знаки линейных эффектов различны. Тогда приходится учитывать численные значения коэффициентов и жертвовать самым малым эффектом.
Иногда приходится учитывать технологические соображения: например, эксперимент в одной области факторного пространства дороже (или труднее), чем в другой.
Пример 2. Рассмотрим один из простейших примеров интерпретации, связанной с гипотезами о механизме действия факторов (см. стр. 118). Изучалось влияние трех факторов на выход сульфадимизина. По поводу влияния концентрации уксусной кислоты х3 априори выдвигалась следующая гипотеза. Предполагалось, что уксусная кислота является растворителем, не участвующим в процессе. Из уравнения регрессии
у = 85,975 f 2,588*!-f 0,568:г2 + 1,125*, — 0,588ад, — 0,Шх2х3, (s{4} = = 0,28)
видно, что существенным оказался не только Ь3, но также Ь13 и Ь23. Этот факт Ставит под сомнение первоначальную гипотезу, и можно предположить, что уксусная кислота активно участвует в процессе.
Заканчивая этот параграф, упомянем еще об интерпретации эффектов взаимодействия высоких порядков. Если значимым оказался эффект взаимодействия трех факторов, например хгх2х3, т0 его можно интерпретировать следующим образом. Этот эффект может иметь знак плюс, если отрицательные знаки будут у четного числа факторов (ноль или любые два). Знак минус будет, если нечетное число факторов имеет знак минус (все три или любой один). Это правило распространяется на взаимодействия любых порядков. Пользуются еще таким приемом. Произведение двух факторов условно считают одним фактором и сводят трехфакторное взаимодействие к парному и т. д.
Мы сказали, что интерпретация результатов — это перевод с одного языка на другой. Такой перевод обеспечивает взаимопонимание между статистиком и экспериментатором, работающими совместно над задачами оптимизации. Интерпретация уравнения регрессии важна не только для понимания процесса, но и для принятия решений при оптимизации.
11.2. Принятие решений после построения модели процесса
Нам придется принимать решения в сложных ситуациях. Решения зависят от числа факторов, дробности плана, цели исследования (достижение оптимума, построение интерполяционной формулы) и т. д. Количество возможных решений по примерной оценке достигает нескольких десятков тысяч. Поэтому мы будем рассматривать только наиболее часто встречавшиеся нам случаи и выделим «типичные» решения. Положение здесь сложнее, чем в случае принятия решений о выборе основного уровня и интервалов варьирования факторов (гл. 6), где удалось рассмотреть все варианты. Ситуации будем различать по адекватности и неадекватности модели, значимости и незначимости коэффициентов регрессии в модели, информации о положении оптимума.
Обсудим сначала принятие решения для адекватного линейного уравнения регрессии.
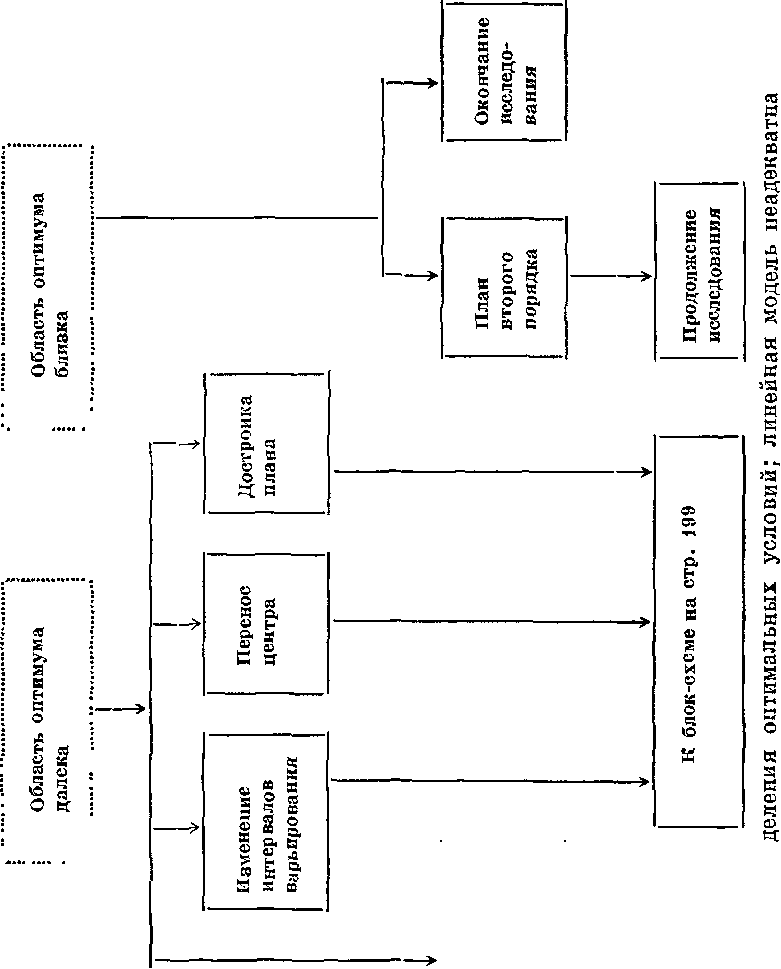
Линейная модель адекватна. Здесь возможны три варианта ситуации: 1) все коэффициенты регрессии значимы; 2) часть коэффициентов регрессии значима, часть незначима; 3) все Коэффициенты регрессии незначимы.
В каждом варианте оптимум может быть близко, далеко или о его положении нет информации (неопределенная ситуация).
Рассмотрим первый вариант.
Если область оптимума близка, возможны три решения: окончание исследования, переход к планам второго порядка и движение по градиенту.
Переход к планированию второго порядка дает возможность получить математическое описание области оптимума и найти экстремум. Хотя мы и не рассматриваем вопросы построения планов второго порядка, эту возможность надо также учитывать. Подробные рекомендации по применению планирования второго порядка вы найдете, например, в руководстве [1].
Движение по градиенту используется при малой ошибке опыта, поскольку на фоне большой ошибки трудно установить приращение параметра оптимизации.
Решение при неопределенной ситуации или удаленной области оптимума одно и то же: движение по градиенту.
Второй вариант — часть коэффициентов регрессии значима, часть незначима. Вам пока придется поверить, что движение по градиенту наиболее эффективно, если коэффициенты значимы. Поэтому выбираются решения, реализация которых приводит к получению значимых коэффициентов. На этом этапе важно выдвинуть гипотезы, объясняющие незначимость эффектов. Это может быть и неудачный выбор интервалов варьирования, и включение (из осторожности) факторов, не влияющих на параметр оптимизации, и большая ошибка опыта, и т. д. Решение зависит от того, какую гипотезу мы предпочитаем.
Если, например, выдвинута первая гипотеза, то возможно такое решение: расширение интервалов варьирования по незначимым факторам и постановка новой серии опытов. Изменение интервалов варьирования" иногда сочетают с переносом центра ^эксперимента в точку, соответствующую условиям наилучшего опыта. Невлияющие факторы стабилизируются и исключаются из дальнейшего рассмотрения. Другие возможные решения для получения значимых коэффициентов: увеличение числа параллельных опытов и достройка плана. Увеличение числа параллельных опытов приводит к уменьшению дисперсии воспроизводимости и соответственно дисперсии коэффициентов регрессии. ()пыты могут быть повторены либо во всех точках плана, либо в некоторых.
Достройка плана осуществляется несколькими способами; методом «перевала» — у исходной реплики Изменяют знаки на обратные (в этом случае основные эффекты оказываются не смешанными с парными эффектами взаимодействия); переходом к полному факторному эксперименту; переходом к реНлике меньшей дробности; переходом к плану второго порядка (если область оптимума близка).
Реализация любого из, этих решений требует значительных экспериментальных усилий. Поэтому иногда можно и не следовать строго правилу «двигайтесь по всем факторам», а пойти на некоторый риск и двигаться только по значимым факторам.
Наконец, если область оптимума близка, то возможно принятие таких же решений, как и в случае значимости всех коэффициентов регрессии.
Рассмотрим последний вариант: линейная модель адекватна, все коэффициенты регрессии незначимы (кроме Ь0). Чаще всего это происходит вследствие большой ошибки эксперимента или узких интервалов варьирования. Поэтому возможные решения направлены прежде всего на увеличение точности эксперимента и расширение интервалов варьирования. Увеличение точности, как вй уже знаете, может достигаться двумя путями: благодаря улучшению методики проведения опытов или вследствие постановки параллельных опытов.
Если область оптимума близка, то возможно также окончание исследования.
В заключение приведем блок-схему принятия решения в задаче определения оптимальных условий, линейная модель адекватна (рис. 28). В блок-схеме пунктирными линиями обведены ситуации, сплошными линиями — принимаемые решения.
Пример 3. При определении оптимальных условий технологического' процесса получения волокна из полипропилена в качестве независимы^ переменных были выбраны: х1 — температура расплава, °С; — давление расплава, кг/см2', х3 — скорость намотки на бобину, м/мин] Ж4 — температура нагревателей, °С; хй — скорость вытягивания, м/мин; 2в — кратность вытягивания.

|
Параметр оптимизации — прочность, волокна. Условия, матрица планирования и результаты этих дорогостоящих и трудоемких опытов приведены в табл. 11.1 [2].
Таблица 11.1
Матрица планирования и результаты опытов
|
Здесь использована 1/8-реплика от полного факторного эксперимента 2е с генерирующими соотношениями xi=x1x2x3, х6-~ —хухг, хв-= —х2х3.
Получены следующие оценки коэффициентов регрессии и ошибки в их определении:
= 56,500, Ь3= 0,125, Ье = 2,500,
bj = 2,700, fc4 = —3,500, s^ =1,060.
6а= 0,0749, fc6= 0,575.
Линейное уравнение регрессии адекватно. Из шести коэффициентов регрессии три коэффициента (bv blt fre) значимы. Информации о положении области оптимума нет.
Рассмотрим два варианта принятия решения: 1) движение по градиенту; 2) расширение интервалов варьирования.
Оценим первый вариант. Из шести коэффициентов регрессии только три оказались значимыми, так что движение может быть неэффективным. Далее применена 1/8-реплика от полного факторного эксперимента; смешанность эффектов высока, и не исключено, что оценки коэффициентов регрессии являются суммарными оценками нескольких значимых эффектов. С другой
стороны, устранение незначимости линейных эффектов требует постановки цовых опытов, а они длительны и дороги. В крутом восхождении мы рискуем напрасно поставить только 2—3 опыта. Поэтому решение о движении по градиенту кажется нам разумным.
В данном примере было принято решение о движении по градиенту.
Второй вариант — с помощью дополнительных опытов устрапить незначимость эффектов. Действительно, только три коэффициента из шести оказались значимыми, эффекты смешаны довольно сильно: движение по градиенту может быть неэффективным. Поэтому решение об изменении интервалов варьирования кажется правильным. Единственное, что не учтено этим решением, — длительность и трудоемкость опытов. Изменение интервалов варьирования требует не менее восьми дополнительных опытов. Это трудно осуществить на практике.
Пример 4. В задаче ионообменного разделения неодима и празеодима (стр. 70) получено адекватное уравнение регрессии: р=88,0—2,0а-!—4,5х2; jr/,\—0,30. Все коэффициенты регрессии значимы, область оптимума близка (наилучший опыт серии г/х=95%). Цель исследования — получение выхода 99—100%, число опытов лимитировано. Варианты решения: 1) движение по градиенту; 2) окончание исследования; 3) переход к плану второго порядка.
Первый вариант — движение по градиенту. Это наиболее приемлемое решение. Несмотря на близость области оптимума, целесообразно увеличить выход на несколько процентов за счет реализации небольшого (2—3) числа опыгов. Этой цели отвечает решение о движении по градиенту, тем более что постановка плана второго порядка потребовала бы проведения еще не менее 5 опытов.
Второй вариант — исследование можно закончить. Закончить или продолжить исследование — решает экспериментатор, исходя из тех задач, которые перед ним стоят. Здесь представлялось важным увеличить выход на несколько процентов по сравнению с лучшим опытом серии (^=95%).
Третий вариант — следует переходить к планированию второго порядка. По условию задачи важно было увеличить выход за счет двух-трех опытов. Этому отвечает движение по градиенту.
В данной задаче было использовано движение по градиенту, расчет которого приведеп в гл. 12.
Остается только упомянуть о задаче построения интерполяционной формулы: цель исследования достигнута, если получена адекватная модель.
Перейдем к следующему разделу — принятие решения в случае неадекватной линейной модели.
Линейная модель неадекватна. Если линейная модель неадекватна, значит не удается аппроксимировать поверхность отклика плоскостью. Формальные признаки (кроме величины F-кри- терия), по которым можно установить неадекватность линейной модели, следующие.
1. Значимость хотя бы одного из эффектов взаимодействия.
2. Значимость суммы коэффициентов регрессии при квадратичных членах Оценкой этой суммы служит разность между Ъ0 и значением зависимой переменной в центре плана у0. Если разность превосходит ошибку опыта, то гипотеза о незначимости-коэф- фициентов при квадратичных членах не может быть принята. Однако надо учесть, что сумма может быть незначима и при значимых квадратичных эффектах, если они имеют разные знаки.
Для неадекватной модели мы не будем делать различия между случаями значимых и незначимых линейных коэффициентов регрессии, поскольку решения для них обычно совпадают.
Решения, принимаемые для получения адекватной модели: изменение интервалов варьирования факторов, перенос центра плана, достройка плана.
Наиболее распространенный прием — изменение интервалов варьирования. Он, конечно, требует постановки новой серии опытов. Иногда отказываются от построения адекватной модели, чтобы ценой нескольких опытов проверить возможность движения по градиенту. Это решение нельзя считать достаточно корректным. Движению по градиенту обычно предшествует оценка кривизны поверхности отклика (по сумме коэффициентов при квадратичных членах) и сопоставление величин линейных эффектов и эффектов взаимодействия. Если вклад квадратичных членов и эффектов взаимодействия невелик, то решение о движении по градиенту представляется возможным.
Еще одно решение: включение в модель эффектов взаимодействия и движение с помощью неполного полинома второго порядка. Этот прием связан с получением и анализом уравнений второго порядка. Направление градиента будет меняться от точки к точке.
Если область оптимума близка, то, как и в блок-схеме рис. 28, возможны варианты окончания исследования и перехода к построению плана второго порядка.
На рис. 29 приведена блок-схема принятия решений в задаче оптимизации для случая, когда линейная модель неадекватна.
Пример 5. Оптимизировался процесс получения фармацевтического препарата (карбометоксисульфанилгуанидина). В качестве факторов были выбраны: хх — отношение растворителя к основному веществу, г/л; х2 — температура реакционной массы, °С; х3 — время реакции, мин.
Параметр оптимизации — выход продукта в процентах. Условия, матрица планирования и результаты опытов приведены в табл. 11.2.
Получены следующие результаты:
60 = 23,15, Ь3 = 9,47, bi3 = 3,64, ^{Ь}=0,12,
61= 1,92, 612= 0,04, Ьш = ~ 0,87, s|y} = 0,97.
62 = 10,35, Ь13 = —0,91,
Линейное уравнение регрессии оказалось неадекватным: Faicn=32,74 при табличном значении 4,12. Область оптимума далека.
Варианты решения: 1) постановка новой серии опытов, связанная с изменением интервалов варьирования и переносом центра; 2) движение по градиенту.
| < я t" ■< м м в н ■< а S3 л ч в н о и < S3 е в S3 а ч |
| и | |
| я | |
| св и Я w | в- в Е 1 |8 f |
| к >& | |
| О | и О |

Таблица 11.2
Матрица планирования и результаты опытов
|
Изменение интервалов варьирования факторов и попытка получения адекватной модели — в данной ситуации вполне приемлемое решение. Интервалы варьирования нужно изменить по факторам х2 и х3. Изменение интервалов можно дополнить перенесением центра эксперимента в условия опытов 1 или 8, давших лучшие результаты.
Таким образом, это решение требует реализации еще восьми опытов.
Проанализируем второе вполне возможное решение. Три эффекта взаимодействия (613, Ьаз, 6Ш) оказались значимыми, так что постановка новой серии опытов с уменьшением интервалов варьирования представляется разумным решением. Но в то же время линейные эффекты не смешаны с эффектами взаимодействия, и их вклад в уравнение регрессии значительно превышает вклад взаимодействий. Напомним, что опыты дороги. Поэтому решение о проведении двух-трех опытов крутого восхождения более всего в данной ситуации соответствует цели достижения максимального выхода с минимальными затратами, хотя и существует риск не получить улучшения результатов.
При выполнении этой работы исследователи выбрали движение но градиенту и улучшили результаты в два раза (см. гл. 12).
Особый случай возникает при использовании насыщенных планов. При значимости всех коэффициентов регрессии ничего нельзя сказать об адекватности или неадекватности модели. Движение по градиенту в такой ситуации показывает правильность предположения, что коэффициенты регрессии являются оценками для линейных эффектов.
Остановимся теперь на задаче построения интерполяционной формулы.
14.3. Построение интерполяционной формулы.
Линейная модель неадекватна
Первое, что следует сделать при решении этой задачи,—включить в уравнение эффекты взаимодействия. Конечно, такое решение возможно, если был применен ненасыщенный план. После введения эффектов взаимодействия может не хватать степеней свободы и потребуется реализация еще двух-трех опытов внутри области эксперимента для проверки гипотезы адекватности.
Все остальные способы построения интерполяционной формулы связаны с необходимостью проведения новых опытов. Один из них — достройка плана. Используются все те же приемы, что и при устранении незначимости коэффициентов регрессии (стр. 196): метод «перевала», достройка до полного факторного эксперимента, до дробной реплики, для которой ранее смешанные эффекты становятся «чистыми», достройка до плана второго порядка.
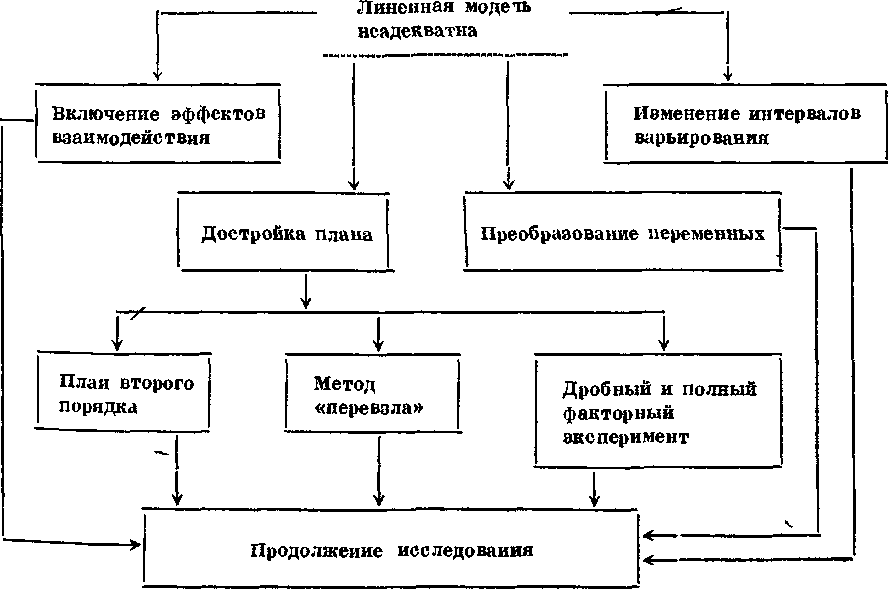 Рис. 30. Принятие решений в задаче построения интерполяционной формулы; линейная модель неадекватна
Рис. 30. Принятие решений в задаче построения интерполяционной формулы; линейная модель неадекватна
|
Еще один, хотя и не очень распространенный прием,— преобразование зависимых и независимых переменных, о котором упоминалось в гл. 2. Однако его подробное рассмотрение выходит за рамки нашей книги.
Наконец, если не удалось все-таки получить адекватную модель, то остается разбить область эксперимента на несколько подобластей и описать отдельно каждую из них. Это требует уменьшения интервалов варьирования факторов.
Приведем блок-схему принятия решений в задаче построения интерполяционной формулы для случая, когда линейная модель неадекватна (рис. 30). Если линейная модель адекватна, то задача решена.
Пример 6. В качестве факторов при построении математической модели ящичного экстрактора были выбраны: хх — диаметр турбинки, мм; х2 — скорость вращения турбинки, об/мин; х3 —температура, °С; ^ — концентрация свободной-кислоты в водном растворе, гзкв/л; хь — высота слоя жидкости в ячейке, мм; хв — соотношение фаз в эмульсии.
Параметр оптимизации — продолжительность полного расслаивания в мин. Условия, матрица планирования и результаты опытов приведены в табл. 11.3. Использована 1/4-реплика от полного факторного эксперимента 26. Линейное уравнение регрессии оказалось неадекватным. Затем были введены три несмешанных между собой эффекта взаимодействия факторов, имеющих наибольшую абсолютную величину
0=12,16+ 0,53*! f 0,53*2 —l,3fe*s — 3,22Ж4+ 1,44*5 — 0,62зс6 — — 0,84*j*4 — 0,50х1хв — 0,78*2*4,
Это уравнение адекватно описывает процесс S|^=0,39. Рассчитанное значение FgKclI=2,A при табличном значении F =2,7. Уравнение было использовано при проектировании промышленного аппарата.
Вот один из возможных приемов построения интерполяционном модели.
11.4. Резюме
Перевод модели с абстрактного математического языка на язык экспериментатора мы назвали интерпретацией модели. Интерпретация — сложный процесс, который проводится в несколько этапов. Он включает оценку величины и направления влияния отдельных факторов и их взаимодействий, сопоставление влияния совокупности факторов, проверку правильности априорных представлений и в некоторых случаях проверку и выдвижение гипотез о механизме процесса.
Сочетание возможных действий с различными экспериментальными ситуациями приводит к десяткам тысяч возможных решений. Поэтому обсуждаются только «типичные» решения. Ситуации различаются по адекватности и неадекватности модели, значимости и незначимости коэффициентов регрессии, положению оптимума.
Для линейной адекватной модели со значимыми коэффициен-
Таблица 11.3
Матрица планирования и результаты опытов
|
тами регрессии возможны: движение по градиенту, план второго порядка, окончание исследования. Если часть коэффициентов регрессии незначима, то возможен выбор одного из решений, позволяющих получать коэффициенты регрессии значимыми: изменение интервалов варьирования, перенос центра плана, отсеивание незначимых факторов, параллельные опыты, достройка плана. Кроме того, остается движение по градиенту, а если область оптимума близка, то реализация плана второго порядка или окончание исследования.
Наконец, если все коэффициенты незначимы, то выбираются решения по реализации плана второго порядка или окончанию исследования (область оптимума близка) либо решения, позволяющие получать значимые коэффициенты регрессии (область оптимума далека и неопределенная ситуация).
Линейная модель неадекватна. Если область оптимума близка, то исследование либо заканчивается, либо реализуется план второго порядка. Такие решения, как изменение интервалов варьирования, перенос цоптра плана, достройка плапа, двпжепио по градиенту, применяются при любом положении оптимума. Возможно включение в модель эффектов взаимодействия факторов и движение с помощью неполного полинома второго порядка, а также оценка квадратичных эффектов для получения информации о кривизне поверхности отклика перед движением по градиенту.
Наконец, если поставлена задача построения интерполяционной формулы, то на получении адекватной модели исследование заканчивается, а в случае неадекватной модели принимается одно из следующих решений: включение в модель эффектов взаимодействия, достройка плана, преобразование переменных, изменение интервалов варьирования.
Литература
1. В. В. Налимов, II. А. Чернова. Статистические методы планирования экстремальных экспериментов. М., «Наука», 1965.
2. Н. С. Иванов, Е. Н. Марина, Д. Ф. Филъберт и др. Применение математической статистики при исследовании процесса формования и вытягивания полипропиленового волокна. В сб. «Карбоцепные волокна». М., Химия, 1966.
Глава двенадцатая
КРУТОЕ ВОСХОЖДЕНИЕ ПО ПОВЕРХНОСТИ ОТКЛИКА
Куда ведешь, тронинка милая?
Из песий
Решения, которые обсуждались в предыдущей главе, направлены на то, чтобы обеспечить эффективное движение по градиенту. Давайте посмотрим, как па практике осуществить это движение.
12.1. Движение по градиенту
Посмотрите на рис. 31. На нем изображены кривые равного выхода поверхности отклика для двух независимых переменных. Они подобны линиям равной высоты на географических картах. Поверхность отклика имеет вид холма с вершиной в точке «О». Если попытаться попасть в окрестность этой точки из точки А с помощью одного из вариантов однофакторного эксперимента, то мы сначала должны стабилизировать первый фактор, например Xj, и изменять в направлении АС второй фактор до тех пор, пока увеличивается выход. За точкой С выход падает, и поэтому в ней сыбилизируем х2 и изменяем х1 в направлении CD по такому же правилу и т. д.
Не кажется ли вам, что путь к вершине довольно извилист? Он сыновится еще более трудоемким при возрастании числа независимых переменных. Наиболее короткий путь к вершине — направление градиента функции отклийа. На рис. 31 это направление ЛВ, перпендикулярное линиям уровня. Градиент непрерывной однозна
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...