
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Описание установки и теория метода
Математический маятник представляет собой массивный шарик небольшого размера, подвешенный на длинной двойной нити, чтобы колебания происходили строго в одной плоскости (рисунок 5.5).

Рисунок 5.5
На перекладине BC подвешен на двойной нити шарик А. Длину математического маятника можно изменять, натягивая нить на барабан. Периоды колебаний математического маятника Т1 и Т2 определяются при разных длинах l1 и l2 по формуле (5.12)
Т1 = 2p 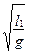 , Т2 = 2p
, Т2 = 2p  (5.13)
(5.13)
Возводим в квадрат Т1 и Т2
Т1 2 = 4p 2  , Т2 2 = 4p 2
, Т2 2 = 4p 2 
и получим для ускорения свободного падения g следующее соотношение:
g = 4p 2  . (5.14)
. (5.14)
Так как в формулу (5.14) входит разность длин маятников, то можно измерить расстояние точки 0 до точки подвеса шарика (×)А (рисунок 5.5).
Порядок выполнения работы
1. Установить максимальную длину математического маятника l1.
2. Определить с помощью секундомера время t 20-30 N полных колебаний и вычислить период колебаний Т1 = 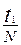 маятника. Измерение повторить не менее 3 х раз. Углы отклонения маятника должны быть 40 – 60.
маятника. Измерение повторить не менее 3 х раз. Углы отклонения маятника должны быть 40 – 60.
3. Поднять шарик на 15-20 см, наматывая нить на барабан, закрепив его стопорным винтом, и определить его длину l2
4. Определить период колебаний маятника Т2 = 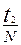 . Измерение произвести не менее 3х раз.
. Измерение произвести не менее 3х раз.
5. Рассчитать абсолютную и относительную погрешности ускорения свободного падения и сравнить с g0 = 9,81 м/c2.
Результаты измерений и вычислений занести в таблицу 5.1.
Таблица 5.1
| № изм. | N число колеб. | l1 | t1 | T1 | l2 | t2 | T2 | g | ágñ | g |
| 1 | ||||||||||
| 2 | ||||||||||
| 3 |
5.4 Контрольные вопросы
1. Какой процесс называется гармоническим колебанием?
2. Что называется физическим маятником?
3. Вывести формулу периода математического маятника.
4. Зависит ли период колебаний математического маятника от его массы.
5. Почему для определения силы тяжести измеряют периоды и разность длин двух математических маятников, а не используется один маятник, вычисляя g по формуле
g = 4p 2 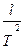
6. Вывести формулы погрешностей для всех определяемых величин.
6. Почему формулой Т = 2p  можно пользоваться только в том случае, когда амплитуда колебаний маятника мала?
можно пользоваться только в том случае, когда амплитуда колебаний маятника мала?
Техника безопасности
1. При работе с математическим маятником следить за тем, чтобы нити не закручивались и не соскальзывали с барабана.
2. Углы отклонения маятников от положения равновесия не должны превышать 70.
Лабораторная работа. ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗОВ ПО МЕТОДУ КЛЕМАНА И ДЕЗОРМА
Цель работы: определение отношения молекулярной теплоемкости воздуха при постоянном давлении СР к молекулярной теплоемкости при постоянном объеме 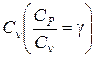 .
.
Основные понятия и закономерности
Теплоемкостью вещества называют физическую величину, равную количеству тепла, необходимого для нагревания вещества на один градус 1 °С (или на 1 К).
 , (6.1)
, (6.1)
где dQ – бесконечно малое количество тепла, полученное веществом,
dT – бесконечно малое изменение (приращение) его температуры.
Теплоемкость зависит от массы нагреваемого тела. Количество тепла, которое надо сообщить единице массы этого вещества, чтобы повысить его температуру на 1 К (или 1 °С) называют удельной теплоемкостью с:
 . (6.2)
. (6.2)
Молярной теплоемкостью С вещества называют физическую величину, численно равную количеству тепла, необходимого для нагревания одного моля вещества на один градус:
 , (6.3)
, (6.3)
где 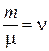 – количество вещества – число молей в данной массе.
– количество вещества – число молей в данной массе.
Из соотношений (6.2) и (6.3) можно определить количество теплоты, получаемое телом:
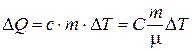 (6.4)
(6.4)
и связь удельной и молярной теплоемкостей с и С:
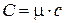 , (6.5)
, (6.5)
где m – масса одного моля газа.
У твердых и жидких тел величина теплоемкости не зависит от условий их нагревания.
Теплоемкость газов сильно зависит от условий нагревания. Это связано с тем, что подводимое к газу тепло расходуется не только на повышение внутренней энергии газа, которое обуславливает повышение его температуры, но и на совершение работы против внешних сил.
При нагревании газа при постоянном объеме рассматривается теплоемкость при постоянном объеме СV, при постоянном давлении СP. Чтобы установить различие между теплоемкостями Сp и СV, связь между ними, воспользуемся первым началом (законом) термодинамики – всеобщий закон сохранения и превращения энергии, который формулируется так:
количество теплоты dQ, сообщаемое системе, расходуется на увеличение внутренней энергии dU и на совершение системой работы dА над внешними телами (против внешних сил):
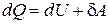 , (6.6)
, (6.6)
где U – внутренняя энергия системы, т.е. сумма всех видов кинетической и потенциальной энергии всех составных частей системы: молекул, атомов, электронов и т.д.
Для идеального газа внутренняя энергия представляет только кинетическую энергию хаотического, теплового движения молекул и равна:
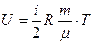 ,
,
где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа),
i = 3 для одноатомного газа – поступательные степени свободы,
i = 5 для двухатомного газа – три поступательные и две вращательные степени свободы,
i = 6 для трех и многоатомных газов – три поступательные и три вращательные степени свободы.
Работа газа против сил внешнего давления равна:
 , (6.7)
, (6.7)
где P – внешнее давление,
dV – приращение объема газа.
Работа dА и теплота dQ – две формы передачи энергии от одного тела к другому.
Рассмотрим применение первого начала термодинамики к изопроцессам для данной массы газа. Изопроцессами называются термодинамические процессы, происходящие при постоянном значении одного из параметров состояния (P, V, T).
1. Изохорический процесс
Изохорический процесс протекает при постоянном объеме V = const, т.е. dV = 0, следовательно, dA = pdV = 0.
Первое начало термодинамики для этого процесса имеет вид:
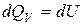 , (6.8)
, (6.8)
Тепло, подводимое к системе, идет на увеличение ее внутренней энергии (нагревание газа) и из соотношения (6.2) равно:
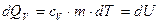 , (6.9)
, (6.9)
где сV – удельная теплоемкость при постоянном объеме – количество тепла, которое идет на нагревание 1 кг газа на 1 К при постоянном объеме.
Молярная теплоемкость при постоянном объеме CV – теплоемкость одного моля:
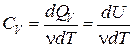 , (6.10)
, (6.10)
отсюда изменение внутренней энергии для любой массы m равно:
 . (6.11)
. (6.11)
Приращение внутренней энергии идеального газа равно:
 , (6.12)
, (6.12)
где i – число степеней свободы (число независимых перемещений, определяющих состояние молекул газа),
i = 3 для одно атомного газа – поступательные степени свободы,
i = 5 для двух атомного газа – три поступательные и две вращательные степени свободы,
i = 6 для трех и много атомных газов – три поступательные и три вращательные степени свободы.
Поэтому
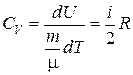 . (6.13)
. (6.13)
2. Изобарический процесс
Изобарический процесс – процесс, протекающий при постоянном давлении Р = const, dP = 0.
Первое начало термодинамики для этого процесса запишется так:
 . (6.14)
. (6.14)
Тепло, подводимое к системе, идет на увеличение внутренней энергии dU и на совершение газом работы над внешними телами dA = PdV.
Из определения молярной теплоемкости (6.3) имеем:
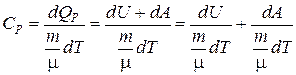 ,
,
где  .
.
Следовательно, получим
 . (6.15)
. (6.15)
Найдем значение  для одного моля.
для одного моля.
Запишем уравнение Клапейрона-Менделеева для одного моля газа
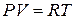 . (6.16)
. (6.16)
Изменение температуры газа при P = const, прямо пропорционально изменению объема dV, т.е.
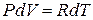 ,
,
где  - работа газа.
- работа газа.
Следовательно,
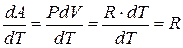 , (6.17)
, (6.17)
где R – универсальная газовая постоянная.
Учитывая, соотношения (6.15) и (6.17), имеем:
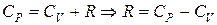 (6.18)
(6.18)
– уравнение Майера устанавливает связь между молярными теплоемкостями СР и СV.
Из соотношения (6.17) можно выяснить физический смысл универсальной газовой постоянной – она численно равна работе, совершаемой одним молем газа в результате нагревания на 1 К при постоянном давлении.
Учитывая (6.13) и (6.18), получим:
 . (6.19)
. (6.19)
При нагревании 1 моля газа на 1 К при изобарическом процессе часть теплоты CV идет на увеличение внутренней энергии, и часть, равная R, – на работу против внешних сил.
3. Изотермический процесс
Изотермический процесс – процесс, протекающий при постоянной температуре T = const, dT = 0, P×V = const.
Изменение внутренней энергии  .
.
Первое начало термодинамики для этого процесса:
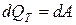 . (6.20)
. (6.20)
Тепло в этом случае идет только на совершение работы против внешних сил (расширение газа).
В термодинамике, кроме изопроцессов, рассматривается адиабатический процесс.
4. Адиабатический процесс
Адиабатический процесс – процесс, протекающий в условиях полной теплоизоляции, т.е. количество теплоты, получаемое газом равно нулю:
 , (6.21)
, (6.21)
Из первого начала термодинамики следует, что при адиабатическом процессе работа газа над внешними телами совершается за счет уменьшения внутренней энергии. Если объем газа увеличивается, то его температура уменьшается, так как уменьшается его внутренняя энергия.
Для адиабатического процесса имеет место уравнение Пуассона:
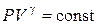 , (6.22)
, (6.22)
где 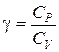 – показатель адиабаты. (6.23)
– показатель адиабаты. (6.23)
Уравнение 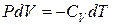 для одного моля – первое начало термодинамики в дифференциальной форме. Получим уравнение адиабатического процесса (уравнение Пуассона) в интегральной форме.
для одного моля – первое начало термодинамики в дифференциальной форме. Получим уравнение адиабатического процесса (уравнение Пуассона) в интегральной форме.
Запишем уравнение Клапейрона-Менделеева для одного моля газа:
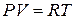 (6.24)
(6.24)
и, дифференцируя это уравнение, имеем:
 . (6.25)
. (6.25)
Преобразуем уравнение (6.21) и (6.25), для этого умножим уравнение (6.21) на R, а уравнение (6.25) на CV:

Сложим эти уравнения почленно:

или 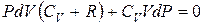 .
.
Учитывая, что 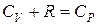 (уравнение Майера), получим:
(уравнение Майера), получим:
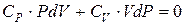 . (6.26)
. (6.26)
Разделим это уравнение на СV:
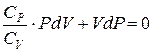 ,
,
где  - показатель адиабаты.
- показатель адиабаты.
И тогда можно записать:
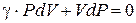 . (6.27)
. (6.27)
Полученное соотношение является так же, как и (6.21), уравнением адиабаты в дифференциальной форме. Делим обе части этого уравнения на P×V:
 , (6.28)
, (6.28)
где 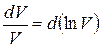 ,
,
 , т.е. дифференциалы натуральных логарифмов V и P, поэтому
, т.е. дифференциалы натуральных логарифмов V и P, поэтому
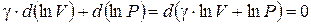 .
.
Величина, стоящая в скобках, является постоянной, так как ее дифференциал равен нулю. Обозначим ее (ln const). Тогда можем записать:

или
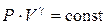 . (6.29)
. (6.29)
Это соотношение – уравнение адиабаты (Пуассона) (6.22).
Используя соотношения (6.13) и (6.19), можно записать значение показателя адиабаты через степени свободы:
 . (6.30)
. (6.30)
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...