Дослідження енергетичної ефективності термодинамічних процесів ідеальних газів

(стор. 106-143)

Характеристики термодинамічного процесу

Зміна параметрів стану не залежить від шляху, за яким термодинамічна систе-ма змінює свій стан. Характеристиками процесу називаються такі величини, зміна яких залежить від характеру, шляху, за яким змінює свій стан система. Їх є чотири:

1. Робота

Розглянемо pv-діаграму.

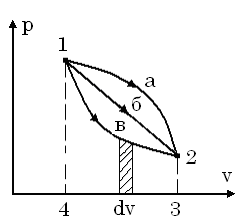
В ній є дві точки, 1 і 2, які характеризу-ють початковий і кінцевий стан системи. Між двома точками можна провести необ-межену кількість кривих ліній, тобто, тер-модинамічних процесів. Таким чином, мо-жна провести 1а, 1б, 1в і так далі. Ми знає-мо, що в pv-діаграмі площа під кривою про-цесу являє собою в деякому масштабі робо-ту. Робота залежить від характеру процесу. Так як з математики відомо, що якщо зна-чення підінтегральної функції залежить від шляху інтегрування, то підінтегральна функція є неповний диференціал.

2. Теплота

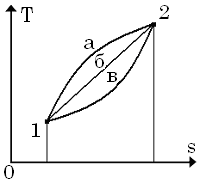
В Ts-діаграмі площа під кривою про-цесу є теплота.

є також неповний диференціал.

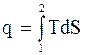
3. Коефіцієнт використання термоди-намічного потенціалу (КВП)

В загальному вигляді термодинаміч-ний потенціал позначається літерою А для маси m кг. КВП позначається літерою , де Х характеризує характер процесу. КВП являє собою відношення зміни термодина-мічного потенціалу в процесі до його значе-ння в початковому стані.

Знак мінус означає, що в процесі перет-ворення енергії хаотичного руху в енергію направленого руху термодинамічний поте-нціал зменшується.

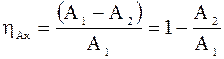
4. Коефіцієнт перетворення енергії (КПЕ)

Позначається , де t – це перша буква від англ. “transformation”. І тому КПЕ є від-ношення роботи процесу до енергії хаотич-ного руху, яка перетворюється в даному процесі.

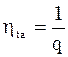для 1 кг

для m кг

.

Лекція 7.

Ізотермічний процес.

1. Дати визначення процесу.

Ізотермічним називають процес, який протікає під час постійної температури.

2. Записати рівняння процесу в pv- і Ts-координатах.

pv=RT, T=const

pv=const

3. Треба зобразити цей процес у pv- і Ts-діаграмах.

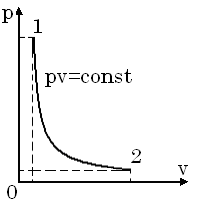
У pv-діаграмі ізотермічний процес зоб-ражується як рівнобока гіпербола.

1-2 – процес розширення.

2-1 – процес стиснення.

У Ts-діаграмі це горизонтальна пряма.

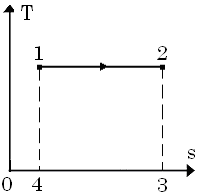
4. Треба записати співвідношення параметрів.

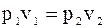
Відношення тисків зворотньопропорці-йне відомим об’ємам.

5. Треба визначити зміну внутріш-ньої енергії в процесі.

, бо .

6. Визначають зміну ентальпії у про-цесі.

7. Визначають зміну ентропії у про-цесі.

Так як , то:

.

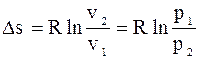8. Знайти теплоту процесу.

З Ts–діаграми бачимо, що:

q=площа (1-2-3-4);

.

9. Знайдемо роботу цього процесу.

;

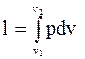pv=RT;

;

;

;

;

; ;

.

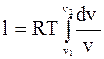10. Зображуємо схему енергобалансу процесу.

Згідно з I законом термодинаміки:

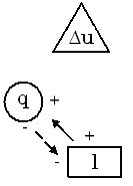
11. Визначаємо коефіцієнт викорис-тання термодинамічного потенціалу в про-цесі (КВП).

У точці 2 термодинамічний потенціал (вільна енергія) рівний нулю:

; .

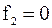Якщо в ізотермічному процесі до робо-чого тіла підвести меншу кількість теплоти q`< площі (1-2-3-4), тоді процес закінчиться у точці 2`. Тобто, не буде використаний весь термодинамічній потенціал f, що приведе до зменшення потужності двигуна.

12. Знаходимо коефіцієнт перетворе-ння енергії в процесі (КПЕ).

Це є відношення енергії направленого руху, яка отримана в процесі, до енергії ха-отичного руху, яка приймала участь у цьо-му процесі.

Ізобарний процес

1. Ізобарним називають процес, який протікає при сталому тиску.

2. Рівняння ізобарного процесу у pv-діаграмі:

Р=const

У Ts-діаграмі

;

;

.

3. Зобразимо цей процес в pv–діаг-рамі та Ts–діаграмі:

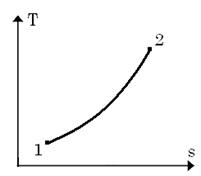
У Ts-діаграмі це логарифмічна крива.

4. Співвідношення параметрів ста-ну.

поділимо на .

Отримаємо: .

5. .

6. .

7. .

8. Теплота процесу:

.

9. 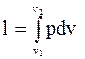; P=const; .

10. Схема енергобалансу

11. КВП:

, де – вільна ентальпія.

12. КПЕ:

.

Ізохорний процес

1. Ізохорним називають процес, який протікає при сталому об’ємі.

2. Рівняння ізохорного процесу в pv-діаграмі: v=const.

У Ts–діаграмі:

.

3. У pv-діаграмі це вертикальна пряма.

У Ts-діаграмі це логарифмічна крива.

1-2 – ізобара P=const.

1-3 – ізохора V=const.

Якщо у Ts-діаграмі через одну і ту ж то-чку проходить і ізобара, і ізохора, то ізобара йде більш полого, а ізохора – більш круто.

; ;

.

4. Написати співвідношення для па-раметрів стану.

поділимо на .

Отримаємо: .

5. .

6. .

7. .

8. .

9. ; ; .

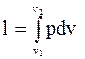d(pv)=vdp+pdv;

pdv=0;

.

10. Схема енергобалансу:

.

11. КВП:

.

12. КПЕ:

.

Це в тому випадку, якщо розглядати роботу розширення:

.

Адіабатний процес

1. Адіабатним називають процес, який протікає без теплообміну з навколиш-нім середовищем.

2. 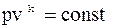у pv-діаграмі.

,

де k – показник адіабати.

У Ts-діаграмі:

.

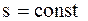У адіабатному процесі ентропія зали-шається незмінною.

3. Зображення цих процесів у pv-ді-аграмі – нерівнобока гіпербола.

Якщо у pv-діаграмі через одну і ту ж то-чку проходить адіабата і ізотерма, то адіа-бата йде більш круто, а ізотерма – більш полого.

4. ;

5. .

6. .

7. .

8. .

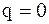9. ; ;

(1)

; ;

(2)

(3)

.

Підставимо замість :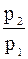

(4)

;

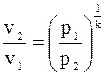(5)

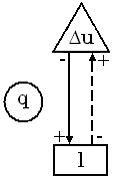
10. Схема енергобалансу.

Політропний процес

1. Політропним називають процес, у якому енергія перетворюється за наступ-ним законом:

2. 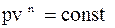, n – показник політро-пи: .

– теплоємність політропного процесу:

.

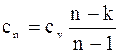3. .

4. Оскільки рівняння політропи ззо-вні схоже з рівнянням адіабати, тільки за-мість k маємо показник політропи n, то всі рівняння адіабатного процесу справедливі для політропного, лише в них треба замі-нити k на n:

Політропний процес перетворюється в основні термодинамічні процеси під час певних значень показника політропи.

Якщо n=0: .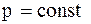

Тобто, маємо ізобарний процес.

n=1: 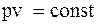– ізотермічний процес.

n=k: 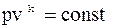– адіабатний процес.

n=∞: ;

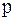настільки більша , що в даному ви-падку ним можемо знехтувати, тому:

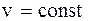– ізохорний процес.

5. .

6. .

7. .

8. .

9. ;

;

;

;

.

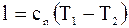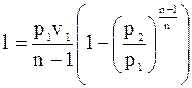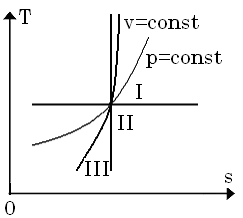
10. У залежності від значення показ-ника політропи, всі процеси розподіляють-ся на три групи:

I. 0<n<1

II. 1<n<k

Політропні процеси другої групи є най-більш ефективні, так як в них робота вико-нується як за рахунок теплоти, яка підво-диться до робочого тіла, так і за рахунок внутрішньої енергії.

III. k<n<∞

Це найневигідніші процеси.

У Ts-координатах:

Тема 3

Механізм отримання роботи

Слід визначити, яким чином змінюєть-ся енергія тіла під час виконання ним ро-боти. Для цього розглянемо Te-діаграму, де зобразимо всі складові частини енергії ро-бочого тіла. По осі ординат відкладемо аб-солютну температуру, а по осі абсцис – ене-ргію в .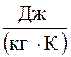

Точка 1 характеризує початковий стан робочого тіла. По осі абсцис відкладемо значення 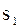точки 1. Відкладемо теплоєм-ність тіла під час сталих об’єму ( ) і тиску ( ). Отримаємо декілька площин.

Площа а-1-6-0 еквівалентна зв’язаній енергії робочого тіла, .

Площа а-2-5-0 – внутрішня енергія ро-бочого тіла .

Тоді, так як 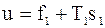, то площа 1-2-5-6 – це є вільна енергія .

Площа а-3-4-0 – рівна ентальпії .

Відома формула Р. Майєра дорівнює відрізку 5-4. Тоді площа 2-3-4-5 еквівалентна .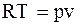

Припустимо, є гаряче джерело , від якого теплота підводиться до робочого тіла в ізотермічному процесі. Тобто, під час під-ведення теплоти стан робочого тіла буде змінюватись за ізотермою 1-2. Прослідкує-мо, які зміни енергії робочого тіла будуть протікати під час цього ізотермічного про-цесу. Перший закон q=* u + l

.

Так як це ізотермічний процес, то:

і .

;

; .

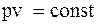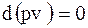У процесі виконується робота . Тоді ро-бимо висновок, що . Ця залежність є чисто кількісна, і вона не відповідає фізич-ному змісту цього процесу. Тобто, прослід-куємо, які ще зміни енергії робочого тіла протікають в ізотермічному процесі. По мі-рі підведення теплоти буде змінюватись стан робочого тіла. Точка 1 буде пересува-тись у напрямку 2, і у точці 2 закінчиться ізотермічний процес. Під час цього буде зменшуватись вільна енергія і збільшува-тись зв’язана енергія. У стані 1` збільши-лась зв’язана енергія до площі а-1`-5`-0, а вільна енергія зменшилася до площі 1`-2-5-5`. У точці 2 вся вільна енергія переходить у зв’язану, і робоче тіло втрачає здатність перетворювати теплоту у роботу. Останню робоче тіло виконує шляхом зміни потенці-альної енергії тиску робочого тіла.

Кількісно 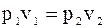, якісно – це різні енергії.

У процесі переходу вільної енергії у зв’язану змінюється потенціальна енергія тиску газу.

Для ізотермічного процесу:

Низка перетворень при виконанні робо-ти робочим тілом:

.

Таким чином, під час підведення тепло-ти робота виконується за рахунок зміни якості енергії робочого тіла.

Лекція 8. 8.10..

(1)

(2)

За виразом Клаузіуса:

Із рівняння (1) видно, що теплота не впливає безпосередньо на зв’язану енергію, і тому між ними нема фізичного зв’язку, а є тільки кількісний. Рівняння (2) для різних основних термодинамічних процесів має рі-зний вигляд, тобто, механізм отримання роботи в різних процесах різний. Так, для ізотермічного процесу ( 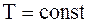) ми бачи-мо, що і 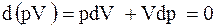. Таким чином, .

З урахуванням зазначеного вище:

(3)

Для ізобарного процесу ( ):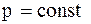

(4)

Для ізохорного процесу ( ):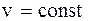

*Q =- dF = TdS+SdT=d(pV) = Vdp=-* L

(5)

Для адіабатного процесу ( ):

;

Вираз 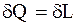не дає можливості прове-сти глибокий аналіз процесів, які прохо-дять під час перетворення енергії.

Тема 4

Водяна пара як реальний газ