
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Глава. СТАТИСТИЧЕСКИЙ АНАЛИЗ НЕКОЛИЧЕСТВЕННЫХ ПЕРЕМЕННЫХ
Зависимость методов измерений связей от уровня измерения переменных
Рассмотренные методы корреляционного и регрессионного анализов разработаны для переменных, измеренных на интервальной шкале или шкале отношений (см. гл.1) Интерваль ные шкалы могут быть построены лишь для количественных признаков, позволяющих не только упорядочить объекты но и рассчитать величину отличия (интервал) одной степени появления признака от другой. Примерами интервальных шкал могут служить шкалы измерения большинства экономических характеристик. В случаях, когда можно указать абсолютный нуль на шкале, мы имеем шкалу отношений. По такой шкале можно сопоставляя переменные, заключить, что одно значение больше (меньше) другого в два раза и т.п. По шкале отношений можно измерять такие характеристики, как стаж работы заработная плата, результаты голосования, потребление природного газа, окупаемость инвестиций и т.п.
Такого рода данные можно упорядочивать, можно приписать цифровые метки каждому варианту ответа, например: 1; 0,5; 0; -0,5; —1. Но это вовсе не означает, что перспективы развития одних предприятий вдвое лучше или хуже перспектив других предприятий, так как эти данные относятся к порядковым. Порядковые данные привлекают все больше внимания в связи с построением рейтингов коммерческих банков, высших учебных заведений, торговых и промышленных органи-
Измерение связи между двумя дихотомическими переменными
Для измерения связи между двумя дихотомическими переменными (т.е. признаками, каждый из которых принимает два значения) данные представляются в виде таблицы сопряженности 2 х 2 (ее называют также четырехпольной таблицей). Например, изучается связь между активностью работы в профсоюзе и уровнем заработной платы (табл. 11.2). В табл. 11.2 показано, как распределились по категориям 100 работников, по которым были получены данные о зара-
Другие меры связей между номинальными переменными
Коэффициенты корреляции рангов
Недостатком коэффициента корреляции рангов является то, что одинаковым разностям рангов могут соответствовать совершенно отличные разности значений признаков (в случае количественных признаков). Поэтому для последних следует считать корреляцию рангов, как и коэффициент знаков Фехнера, приближенными мерами тесноты связи, обладаю-щими меньшей информативностью, чем коэффициент корреляции числовых значений признаков. Рассчитаем коэффициент корреляции рангов по данным табл. 11.11, Ранги присвоены в соответствии со значениями переменных (см. табл. 9.1).
Вычислим коэффициент корреляции рангов Кендэла по Данным табл. 11.12. Таблица 11.12 Ранжирование данных по переменным х и у
для переменных типа «чем больше, тем хуже». Если нельзя отдать предпочтение нескольким объектам, то каждому из них присваивается средний ранг, определяемый как средний арифметический из суммы соответствующих мест («связанные ранги»). Скажем, если нельзя отдать предпочтение второму, третьему и четвертому объектам, то каждому из этих
Таблица 11.13 Расчет коэффициента конкордации
РЕЗЮМЕ
Способы измерения связей между признаками зависят от того, по какой шкале они измерены: номинальной, порядковой, интервальной или шкале отношений. В собираемых статистических данных непрерывно возрастает доля нечисловой информации. Это объясняется несколькими причинами:
Измерение связи между неколичественными переменными основано на таблице сопряженности — двух- или трехмерном распределении единиц совокупности. Если переменные дихотомические, то данные представляются в таблице 2x2 и вычисляются специальные меры связи: коэффициенты ассоциации, коэффициенты контингенции. По таблицам сопряженности т х р вычисляются коэффициенты взаимной сопряженности, основанные на тестовой статистике хи-квадрата. В случае, если нельзя выполнить условия применения статистики хи-квадрат, рекомендуется пользоваться теоретико-информационными мерами связей, основанными на измерении энтропии распределений и количества информации. В качестве мер связей между номинальными переменными используются меры связи: Х-Гутмана, т-Гудмена и Краскала и др. Корреляция между порядковыми переменными измеряется коэффициентом ранговой корреляции. Широко распространены коэффициенты ранговой корреляции Спирмена и Кендэла. Меры связей между неколичественными переменными применяются при обработке данных экспертных опросов. Если экспертам нужно оценить объект не по одному, а по нескольким свойствам, то используется коэффициент конкордации. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 1. Антон Г. Анализ таблиц сопряженности: Пер. с англ. — М.: Финансы и статистика, 1982. 2. Елисеева И. И., Рукавишников В. О. Логика прикладного статистического анализа. — М.: Финансы и статистика, 1982. 3. Информатика в статистике: Словарь-справочник. — М.: Финансы и статистика, 1994. 4. Ниворожкина Л. И., Морозова 3. А. Сборник задач по математической статистике с элементами теории вероятностей. — Ростов-на-Дону: РИНХ, 2002.
|
Последнее изменение этой страницы: 2016-07-28; просмотров: 924
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...
 411
411 412
412 413
413
 415
415
 417
417 418
418 419
419 420
420 421
421 422
422 423
423 424
424 425
425 426
426 427
427 428
428 429
429 430
430 431
431 432
432
 434
434
 436
436 437
437 Примущество коэффициента корреляции рангов состоит в том, что ранжировать можно и по таким признакам, которые нельзя выразить численно: можно проранжировать кандидатов на занятие определенной должности по профессиональному уровню, по умению руководить коллективом, по личному обаянию и т.п. При экспертных оценках можно ранжировать оценки разных экспертов и найти их корреляции друг с другом, чтобы затем исключить из рассмотрения оценки эксперта, слабо коррелированные с оценками других экспертов. Коэффициент корреляции рангов применяется для оценки устойчивости тенденции динамики (см. подразд. 12.9).
Примущество коэффициента корреляции рангов состоит в том, что ранжировать можно и по таким признакам, которые нельзя выразить численно: можно проранжировать кандидатов на занятие определенной должности по профессиональному уровню, по умению руководить коллективом, по личному обаянию и т.п. При экспертных оценках можно ранжировать оценки разных экспертов и найти их корреляции друг с другом, чтобы затем исключить из рассмотрения оценки эксперта, слабо коррелированные с оценками других экспертов. Коэффициент корреляции рангов применяется для оценки устойчивости тенденции динамики (см. подразд. 12.9).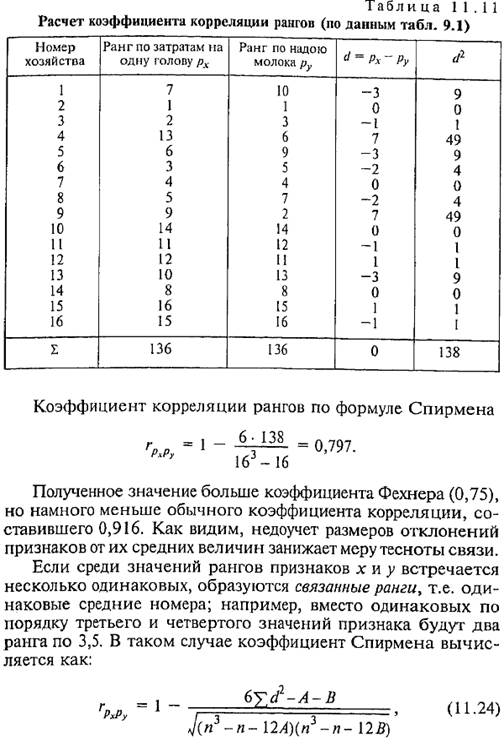 439
439 440
440 Значениям каждой переменной приписываются ранги. Ранг 1 устанавливается наименее важному значению: минимальному — для стимулянт, т.е. для переменных типа «чем больше, тем лучше», и максимальному для дестимулянт, т.е.
Значениям каждой переменной приписываются ранги. Ранг 1 устанавливается наименее важному значению: минимальному — для стимулянт, т.е. для переменных типа «чем больше, тем лучше», и максимальному для дестимулянт, т.е. 442
442