
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Средние показатели тенденции динамики
Средние показатели динамики — средний уровень ряда, средние абсолютные изменения и ускорения, средние темпы роста — характеризуют тенденцию. Они необходимы при обобщении характеристик тенденции за длительный период, по различным периодам и незаменимы при сравнении развития за неодинаковые по длительности отрезки времени, при выборе аналитического выражения тренда. При наличии в динамическом ряду существенных колебаний уровней определение средних показателей тенденции требует использования специальных методов статистики, которые рассматриваются в следующих разделах. В данном разделе рассматриваются только форма, математические свойства средних пока- зателей динамики и простейшие приемы их вычисления, применимые на практике к рядам со слабой колеблемостью. Средний уровень интервального ряда динамики определяется как простая арифметическая средняя из уровней за равные промежутки времени:
В моментном ряду смысл среднего уровня в том, что он характеризует уже не состояние на отдельный момент, а состояние между начальным и конечным моментом учета. Из этого следует, что роль уровней, относящихся к начальному и конечному моментам, существенно иная, чем роль уровней на момент внутри изучаемого отрезка времени. Начальный и конечный уровни находятся на границе изучаемого интервала, они наполовину относятся к предыдущему и последующему интервалам и лишь наполовину к изучаемому. Уровни, отно- сящиеся к моментам внутри осредняемого интервала, целиком относятся только к нему. Отсюда получаем особую форму средней арифметической величины, называемую хронологической средней:
Если известны точные даты изменения уровней моментного ряда, то средний уровень определяется как
Как уже сказано выше, при наличии существенной колеблемости уровней средний абсолютный прирост (изменение), как и средний темп, следует вычислять, отделив сначала тренд от колебаний (соответствующая методика будет изложена ниже). Прямое определение среднего абсолютного прироста по крайним уровням ряда допустимо, если нет существенных колебаний уровней. Например, добыча угля в России довольно равномерно снижалась с 337 млн т в 1992 г. до 232 млн т в 1998 г.1 -------------------------------------- 1 Россия в цифрах. 1996. Статистический сборник / Госкомстат России. — М.: Финансы и статистика, 1996. — С. 297.
Для правильной интерпретации показатель среднего абсолютного изменения должен сопровождаться указанием двух единиц времени: 1) время, за которое он вычислен, к которому относится и которое он характеризует (в нашем примере это 6 лет — 1992—1998 гг.); 2) время, за которое показатель рассчитан, время, входящее в его единицу измерения, — 1 год. Можно рассчитать среднемесячный прирост за пятилетие, среднесуточное изменение за год, за месяц, за квартал.
Среднее ускорение абсолютного изменения применяется реже. Для его надежного расчета даже при слабых колебаниях уровней требуется использовать методику аналитического выравнивания по параболе 2-го порядка (см. подразд. 12.5 и 12.6). Не рекомендуется измерять среднее ускорение без абстрагирования от колебаний уровней. Для более грубого, приближенного расчета среднего ускорения можно воспользоваться средними годовыми уровнями, сглаживающими колебания. Например, среднегодовое производство мяса в Российской Федерации составляло:
Годы Среднегодовое производство мяса, млн т 1976-1980 7,40 1981-1985 8,09 1986-1990 9,68
Абсолютный прирост за второе пятилетие в сравнении с первым составил 0,69 млн т, за третье в сравнении со вторым — 1,59 млн т. Следовательно, ускорение в третьем пятилетии по сравнению со вторым составило: 1,59 - 0,69 = 0,90 млн т в год за пять лет, а среднегодовое ускорение прироста равно: 0,90 : 5 = 0,18 млн т в год за год. Среднее ускорение требует указания трех единиц времени, хотя, как правило, две из них одинаковы: период, на который рассчитан прирост, и время, на которое рассчитано ускорение. Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте (см. подразд. 12.5 и 12.6). Если можно пренебречь колеблемостью, то средний темп определяют как геометрическую среднюю (см. гл. 5) из цепных темпов роста за п лет или из общего (базисного) темпа роста за п лет:
Как отмечалось в гл. 5, применяя для вычисления среднего темпа среднюю геометрическую, мы опираемся на соблюдение фактического отношения конечного уровня к начальному при замене фактических темпов на средние. В практических задачах может потребоваться вычисление среднего уровня при условии соблюдения отношения суммы уровней за период к уровню, принятому за базу. Например, если общий выпуск продукции за пятилетие должен составить 800% к базисному (среднегодовому за предыдущие 5 лет выпуску), или, что то же самое, среднегодовой уровень должен составить 160% к базовому уровню, каков должен быть среднегодовой темп роста выпуска продукции? В 1974 г. украинские статистики А. и И. Соляники предложили следующую приближенную формулу для среднего темпа роста, удовлетворяющую этому условию:
Для нашего примера таблица Л. С. Казинца дает среднегодовой темп роста 116,1% и сумму выпуска в 8,00016 раза больше базисной. Если необходимо определить средний темп изменения исходя из заданной на п периодов суммы абсолютных изменений, то следует использовать формулу:
Интересную задачу представляет определение срока, за который ряд с большим средним показателем динамики, но меньшим начальным уровнем догонит другой ряд с большим начальным уровнем, но меньшим показателем динамики.
Через 11,43 года уровень второго ряда сравняется с первым при сохранении экспоненциальных трендов обоих рядов. |
Последнее изменение этой страницы: 2016-07-28; просмотров: 789
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...

 Методика вычисления среднего уровня моментного ряда при неравных промежутках между моментами является спорной и здесь не рассматривается.
Методика вычисления среднего уровня моментного ряда при неравных промежутках между моментами является спорной и здесь не рассматривается.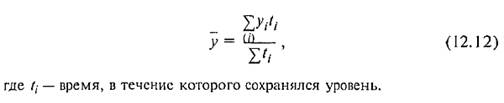 Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления величины базисного абсолютного изменения на число осредняемых отрезков времени от базисного до сравниваемого периода:
Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления величины базисного абсолютного изменения на число осредняемых отрезков времени от базисного до сравниваемого периода:


 464
464
 466
466