
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Условие устойчивости двойственных оценок.
В предыдущем параграфе мы предполагали, что при изменении столбца свободных членов  на величину
на величину  двойственные оценки
двойственные оценки  не изменяются. Выясним теперь, при каких условиях это предположение справедливо. Сформулируем вспомогательное утверждение, справедливость которого известна из курса линейной алгебры.
не изменяются. Выясним теперь, при каких условиях это предположение справедливо. Сформулируем вспомогательное утверждение, справедливость которого известна из курса линейной алгебры.
Теорема 1. Пусть матрица  получена из матрицы
получена из матрицы  методом Гаусса, то есть с помощью последовательности элементарных преобразований. Тогда существует такая матрица
методом Гаусса, то есть с помощью последовательности элементарных преобразований. Тогда существует такая матрица  , что
, что
 . (1)
. (1)
Матрица  называется матрицей перехода от матрицы
называется матрицей перехода от матрицы  к матрице
к матрице  . Отметим, что каждый столбец
. Отметим, что каждый столбец  матрицы
матрицы  получается из соответствующего столбца
получается из соответствующего столбца  матрицы
матрицы  умножением на одну и ту же матрицу
умножением на одну и ту же матрицу  :
:
 , (2)
, (2)
- где  - число столбцов матрицы
- число столбцов матрицы  .
.
Рассмотрим с этой точки зрения решение задачи (1) п.1.8 симплекс-методом. Как мы видели выше (см. пп.1.8-1.9), переход от одной симплекс-таблицы к другой (операция однократного замещения) осуществляется с помощью элементарных преобразований Гаусса, и, следовательно, в силу теоремы 1 с помощью умножения на некоторую матрицу перехода. Рассмотрим подробнее переход от первой симплекс-таблицы к последней симплекс-таблице.
Переместим в первой симплекс-таблице ((4) п.1.8) столбец  с первого на предпоследнее место (для чего это делается, станет ясно позже) и запишем эту таблицу в виде:
с первого на предпоследнее место (для чего это делается, станет ясно позже) и запишем эту таблицу в виде:
| Первая симплекс таблица | |||||||
| X1 | X2 | W1 | W2 | W3 | F | B | |
| -2 | (3) | ||||||
| -1 | |||||||
| -3 | -1 |
Соответствующую матрицу обозначим  . Аналогичным образом запишем последнюю симплекс-таблицу ((11) п.1.8) в виде:
. Аналогичным образом запишем последнюю симплекс-таблицу ((11) п.1.8) в виде:
| Последняя симплекс таблица | |||||||
| X1 | X2 | W1 | W2 | W3 | F | B | |
| 2/3 | -1/3 | ||||||
| -4/3 | 5/3 | (4) | |||||
| 1/3 | 1/3 | ||||||
| 10/3 | 1/3 |
Соответствующую матрицу обозначим  . Матрицу перехода от первой симплекс-таблицы
. Матрицу перехода от первой симплекс-таблицы  к последней симплекс-таблице
к последней симплекс-таблице  обозначим
обозначим 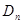 :
:
 . (5)
. (5)
Как было отмечено выше, каждый столбец последней симплекс-таблицы получается из соответствующего столбца первой симплекс-таблицы умножением на матрицу перехода 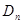 . Поэтому, матрица
. Поэтому, матрица  , содержащаяся в столбцах
, содержащаяся в столбцах  последней симплекс-таблицы (4) получается из соответствующей (единичной) матрицы
последней симплекс-таблицы (4) получается из соответствующей (единичной) матрицы  , стоящей в тех же столбцах первой симплекс-таблицы (3) с помощью умножения на матрицу перехода
, стоящей в тех же столбцах первой симплекс-таблицы (3) с помощью умножения на матрицу перехода 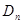 :
:
 .
.
Поскольку  - единичная матрица, то из (5) следует, что
- единичная матрица, то из (5) следует, что
 .
.
Итак, оказалось, что матрица перехода 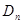 стоит в столбцах
стоит в столбцах  последней симплекс-таблицы
последней симплекс-таблицы  . При этом столбец
. При этом столбец  последней симплекс-таблицы получается из соответствующего столбца первой симплекс-таблицы умножением на матрицу перехода
последней симплекс-таблицы получается из соответствующего столбца первой симплекс-таблицы умножением на матрицу перехода 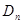 :
:
 (6)
(6)
Векторное равенство (6) равносильно двум равенствам. Первое равенство соответствует первым  строкам равенства (6) и имеет вид:
строкам равенства (6) и имеет вид:
 , (7)
, (7)
где  - (8)
- (8)
- подматрица матрицы исходной системы ограничений, стоящая в столбцах  , которая называется матрицей устойчивости (в таблице (4) она выделена полужирным шрифтом), а
, которая называется матрицей устойчивости (в таблице (4) она выделена полужирным шрифтом), а
 - (9)
- (9)
столбцы свободных членов первой и последней симплекс-таблицы соответственно. Второе равенство соответствует последней строке равенства (6) и фактически означает, что
 , (10)
, (10)
где  - элементы индексной строки последней симплекс-таблицы, стоящие в столбцах
- элементы индексной строки последней симплекс-таблицы, стоящие в столбцах  .
.
Заменим теперь свободные члены  в первой симплекс-таблице на произвольные неотрицательные числа
в первой симплекс-таблице на произвольные неотрицательные числа
 , (11)
, (11)
удовлетворяющие условию устойчивости двойственных оценок:
 . (12)
. (12)
Применим к новой исходной симплекс-таблице те же самые элементарные преобразования, что и к исходной. В результате мы получим новую последнюю таблицу, которая на самом деле окажется симплексной. Действительно, все столбцы этой таблицы кроме, быть может последнего, совпадут с соответствующими столбцами прежней последней симплекс-таблицы, и, следовательно соответствующая система ограничений будет иметь разрешенный вид, а целевая функция будет зависеть только от свободных переменных. Поскольку матрица перехода от первой к последней таблице не изменится, то последний столбец свободных членов, согласно (7) и (11) определяемый равенствами:
 , (13)
, (13)
в силу (12) окажется неотрицательным. Это значит, что на самом деле получена новая симплекс-таблица. При этом все элементы, стоящие в индексной строке кроме, возможно, свободного члена (равного, кстати, значению целевой функции) останутся теми же самыми и, следовательно, будут неотрицательны. Последнее означает, что соответствующее опорное решение является оптимальным. При этом базисные переменные нового оптимального решения будут теми же, что и у старого оптимального решения. Как было отмечено выше, соответствующее новое оптимальное значение целевой функции определяется согласно (10):
 . (14)
. (14)
Пусть новые значения  свободных членов исходной симплекс-таблицы сколь угодно мало отличаются от старых значений
свободных членов исходной симплекс-таблицы сколь угодно мало отличаются от старых значений  (при этом условие (13) предполагается выполненным).
(при этом условие (13) предполагается выполненным).
Тогда новый вектор роста  (15)
(15)
двойственной задачи также бесконечно мало отличается от старого вектора роста  . Из геометрической интерпретации задачи линейного программирования следует, что в этом случае оптимальное решение двойственной задачи достигается в той же угловой точке
. Из геометрической интерпретации задачи линейного программирования следует, что в этом случае оптимальное решение двойственной задачи достигается в той же угловой точке  , то есть двойственные оценки остаются теми же. С другой стороны, по теореме двойственности
, то есть двойственные оценки остаются теми же. С другой стороны, по теореме двойственности
 . (16)
. (16)
Сравнивая (14) и (16), получаем, что
 . (17)
. (17)
Поскольку последнее равенство должно выполняться для любых неотрицательных  , удовлетворяющих условию (12) и достаточно мало отличающихся от
, удовлетворяющих условию (12) и достаточно мало отличающихся от  , то приходим к выводу, что
, то приходим к выводу, что
 . (18)
. (18)
Таким образом, действительно в столбцах балансовых переменных  индексной строки последней симплекс-таблицы содержатся двойственные оценки, как было указано ранее в конце п.1.15.
индексной строки последней симплекс-таблицы содержатся двойственные оценки, как было указано ранее в конце п.1.15.
Итак, мы видим, что при изменениях ресурсов, удовлетворяющих условию устойчивости (12), новое оптимальное решение  может быть найдено из последней симплекс-таблицы, в которой столбец свободных членов
может быть найдено из последней симплекс-таблицы, в которой столбец свободных членов  заменён на новый
заменён на новый  , определяемый (13). При этом двойственные оценки остаются прежними и совпадают с коэффициентами индексной строки последней симплекс-таблицы, стоящими в столбцах балансовых переменных, то есть в базисных столбцах первой симплекс-таблицы.
, определяемый (13). При этом двойственные оценки остаются прежними и совпадают с коэффициентами индексной строки последней симплекс-таблицы, стоящими в столбцах балансовых переменных, то есть в базисных столбцах первой симплекс-таблицы.
Пусть в нашем примере  . Тогда
. Тогда
 ,
,
и (13) будет иметь вид:
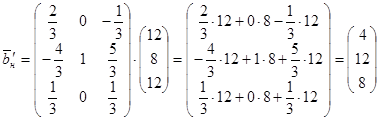 (19)
(19)
Как видим, условие устойчивости (12) выполнено. Новое оптимальное решение 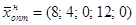 может быть получено из новой последней симплекс-таблицы:
может быть получено из новой последней симплекс-таблицы:
| Последняя симплекс таблица | ||||||
| X1 | X2 | W1 | W2 | W3 | F | B |
| 2/3 | -1/3 | |||||
| -4/3 | 5/3 | |||||
| 1/3 | 1/3 | |||||
| 10/3 | 1/3 | 
|
в которой старый столбец свободных членов  заменен на новый
заменен на новый  . Новое оптимальное значение целевой функции
. Новое оптимальное значение целевой функции  может быть найдено по теореме двойственности:
может быть найдено по теореме двойственности:
 (20)
(20)
Можно также воспользоваться формулой:
 , (21)
, (21)
где  может быть найдено с помощью теоремы двойственности:
может быть найдено с помощью теоремы двойственности:
 , (22)
, (22)
Глава II. Транспортная задача
В предыдущих разделах мы рассматривали симплекс-метод решения задачи линейного программирования. Однако для ряда задач матрица, используемая в симплекс-методе, имеет специальный вид. Поэтому для таких задач разработаны специальные методы решения, позволяющие быстрее найти решение. В этой главе мы разберем одну из таких задач - транспортную задачу.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...