
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Расчет показателей вибропрочности конструкций
Приборной аппаратуры
Конструкция прибора, входящего в состав АПА ЛА, представляет собой сложную механическую систему, состоящую из бесконечно большого числа материальных точек. Поэтому при исследовании динамических процессов, протекающих в конструкциях в условиях механических воздействий, неизбежен переход от реальных систем к упрощенным абстрактным моделям на основе приближений и допущений. Для решения практических задач анализа динамических процессов в конструкциях АПА реальная механическая система заменяется моделью с ограниченным числом степеней свободы, которое определяется структурой конструкции и требуемой точностью результатов [7,21,43].
Применяются два основных вида моделей механических систем: с сосредоточенными массам и связями (упругими и демпфирующими) и с распределенными параметрами.
Так, например, конструкция, совершающая под действием внешней силы колебания вдоль одной координаты, может быть представлена расчетной моделью с одной степенью свободы и сосредоточенными параметрами: массой m, упругой связью с коэффициентом жесткости k и демпфирующей связью с коэффициентом вязкого сопротивления 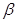 (рис. 5.2,а). В то же время, если сосредоточенная масса совершает сложные пространственные колебания, то такую конструкцию обычно представляют расчетной моделью с n степенями свободы (рис. 5.2,б).
(рис. 5.2,а). В то же время, если сосредоточенная масса совершает сложные пространственные колебания, то такую конструкцию обычно представляют расчетной моделью с n степенями свободы (рис. 5.2,б).
Исходя из определения вибропрочности и анализа динамических процессов, протекающих в элементах конструкций приборов при вибрациях, можно определить следующие условия обеспечения вибропрочности:
- отсутствие в конструкции механических резонансов;
- ограничение амплитуды виброперемещения и виброскорости значениями, исключающими опасные напряжения и усталостные явления в элементах конструкции;
- допустимые значения виброперегрузок в диапазоне частот внешних воздействий должны превышать величины, определенные техническим заданием на разработку конструкции прибора.
Первое условие выполняется, если частота свободных колебаний элементов конструкции лежит за пределами диапазона частот внешних воздействий. Ввиду того, что частота свободных колебании  , где k - жеcткость элемента конструкции; m - масса, то для снижения массы конструкции приемлемым является решение:
, где k - жеcткость элемента конструкции; m - масса, то для снижения массы конструкции приемлемым является решение:  , где
, где 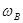 - верхняя граница диапазона частот внешних воздействий.
- верхняя граница диапазона частот внешних воздействий.
Проверка выполнения условия прочности конструкции при вибрации производится на основе приведения динамической задачи к статической. Для этого необходимо найти коэффициент динамичности конструкции  и нагрузку, которая возникает в элементах конструкции:
и нагрузку, которая возникает в элементах конструкции:
 , (5.3)
, (5.3)
где m - масса элемента конструкции; g - ускорение свободного падения;  - вибрационная перегрузка элемента при резонансе.
- вибрационная перегрузка элемента при резонансе.
Затем по формулам сопротивления материалов определяется допустимое напряжение, которое может выдержать элемент в течение заданного срока эксплуатации:
 ,
,
где 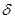 - предельное значение напряжения (предел прочности) для материала ; n - запас прочности.
- предельное значение напряжения (предел прочности) для материала ; n - запас прочности.
Запас прочности обычно устанавливают на основе так называемого дифференциального метода в виде произведения частных коэффициентов:
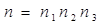 , где
, где 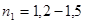 - коэффициент достоверности определения расчетных нагрузок и напряжений;
- коэффициент достоверности определения расчетных нагрузок и напряжений;  - коэффициент, учитывающий степень ответственности детали;
- коэффициент, учитывающий степень ответственности детали;  - коэффициент, учитывающий однородность механических свойств материалов.
- коэффициент, учитывающий однородность механических свойств материалов.
В случае изгибных деформаций напряжение на изгиб
 ,
,
где - изгибающий момент в наиболее опасном сечении элемента конструкции;
- изгибающий момент в наиболее опасном сечении элемента конструкции;  - момент сопротивления при изгибе.
- момент сопротивления при изгибе.
Усталостные разрушения характерны для циклических нагрузок на высоких частотах вибраций и обычно наблюдаются при резонансных колебаниях электрорадиокомпонентов. Чаще всего разрушаются выводы компонентов, так как механические напряжения в определенных сечениях выводов (область изгиба и соединения с контактными площадками коммутационных плат) при вибрациях на резонансной частоте резко возрастают. Если известно максимальное циклическое напряжение в выводах, то по кривой усталости для материала можно определить число циклов до разрушения и, таким образом, составить прогноз долговечности изделия. Количественной оценкой долговечности служит время работы элемента до разрушения выводов
 ,
,
где  - число циклов нагрузки до разрушения;
- число циклов нагрузки до разрушения;  - частота свободных колебаний основного тона элемента.
- частота свободных колебаний основного тона элемента.
Связь между виброперегрузкой  , частотой
, частотой  и амплитудой вибраций Z определяется выражением (5.2). Если, исходя из допустимых напряжений, возникающих в материале элемента конструкции, наложить ограничение на амплитуду вибраций, то получим предельное значение виброперегрузки:
и амплитудой вибраций Z определяется выражением (5.2). Если, исходя из допустимых напряжений, возникающих в материале элемента конструкции, наложить ограничение на амплитуду вибраций, то получим предельное значение виброперегрузки:
 , (5.4)
, (5.4)
Выразив виброперегрузку через виброскорость V, можно найти допустимое значение виброперегрузки при ограничении на виброскорость
 . (5.5)
. (5.5)
Условие вибропрочности конструкции выполняется, если 
Проверку неравенств (5.4) и (5.5) целесообразно проводить или на нижней частоте вынужденных колебаний или на резонансной частоте, где амплитуда вибраций и виброскорость достигают больших значений. Так, например, при низкочастотных вибрациях (  =5 - 50Гц) действующих на АПА, для
=5 - 50Гц) действующих на АПА, для  амплитуда вибраций лежит в пределах 40 - 0,4 мм и изгибные деформации могут вызвать разрушение элемента конструкции. На частоте вибраций 1000 Гц при том же значении виброперегрузки амплитуда вибрации Z=1 мкм. Однако вследствие большого числа циклов колебаний могут возникнуть усталостные явления в материале.
амплитуда вибраций лежит в пределах 40 - 0,4 мм и изгибные деформации могут вызвать разрушение элемента конструкции. На частоте вибраций 1000 Гц при том же значении виброперегрузки амплитуда вибрации Z=1 мкм. Однако вследствие большого числа циклов колебаний могут возникнуть усталостные явления в материале.
Таким образом, оценка вибропрочности конструкций АПА производится по следующим показателям:
- частоте свободных колебаний  ;
;
- допустимому значению напряжения  в материале элементов конструкции и предельному числу циклов нагружения
в материале элементов конструкции и предельному числу циклов нагружения  ;
;
- допустимому значений виброперегрузки  .
.
При расчете частот свободных колебаний элементы конструкций АПА заменяют эквивалентными расчетными моделями, для которых получены аналитические соотношения, связывающие частоту свободных колебаний с параметрами модели.
Основным условием замены является соответствие модели реальной конструкции и минимальное число степеней свободы. Так как резонансные явления могут возникнуть на всех структурных уровнях конструкции, то желательно определять частоты свободных колебаний навесных компонентов, узлов, субблоков и т.д. При этом в зависимости от способа монтажа компоненты могут заменяться расчетными моделями балок или рамы. В качестве расчетных моделей функциональных узлов и других планарных конструкций используется модель пластины.
5.3. Расчет частоты свободных колебании функциональных узлов приборной аппаратуры
Функциональные узлы ПА (модули I структурного уровня конструкции) представляют собой планарные конструкции, состоящие из монтажного основания и смонтированных на нем электрорадиокомпонентов и деталей. Поэтому основной расчетной моделью узлов является прямоугольная пластина при определенном закреплении сторон [55,7,21,43].
Расчет частоты свободных колебаний прямоугольных пластин производится на основе следующих допущений:
- изгибные деформации пластины при вибрации по сравнению с ее толщиной малы, упругие деформации подчиняются закону Гука ;
- пластина имеет постоянную толщину, нейтральный слой пластины не подвержен деформациям растяжения-сжатия;
- материал пластины идеально упругий, однородный и изотропный;
- все прямые, нормальные к поверхности нейтрального слоя до деформации, остаются прямыми и нормальными к ней после деформации.
Дифференциальное уравнение свободных незатухающих колебаний пластины имеет вид
 , (5.6)
, (5.6)
где  - виброперемещение пластины, определяемое в точке с координатами x,y; m - масса пластины;
- виброперемещение пластины, определяемое в точке с координатами x,y; m - масса пластины;  - жесткость пластины на изгиб (цилиндрическая жесткость); Е,
- жесткость пластины на изгиб (цилиндрическая жесткость); Е,  - соответственно модуль упругости и коэффициент Пуассона материала; h - толщина пластины.
- соответственно модуль упругости и коэффициент Пуассона материала; h - толщина пластины.
Точное решение уравнения (5.6) получено для свободных колебаний прямоугольных однородных пластин, две противоположные стороны которых свободно опираются, при любом закреплении двух других сторон.
В случае свободного опирания всех сторон частота свободных колебаний пластины может быть найдена по формуле
 ,
,
где i, j - число полуволн синусоиды, укладывающихся вдоль сторон пластины; a, b - размеры сторон;  - плотность материала пластины.
- плотность материала пластины.
Реальные конструкции функциональных узлов, приводимые к расчетным моделям пластины, по основным параметрам не соответствуют требованиям однородной пластины, а разновидность внутренних структур конструкций ПА ведет к многообразию краевых условий пластин. Поэтому для расчета частоты свободных колебаний функциональных узлов, как правило, используются соотношения, полученные в результате приближенного решения уравнения (5.6) по методу Рэлея или по методу Ритца.
Согласно методу Рэлея частота свободных колебаний  определяется в результате сопоставления выражений для кинетической и потенциальной энергий колебаний системы. Метод позволяет учесть нагружение платы функционального узла установленными на ней компонентами и получить соотношение для расчета частоты свободных колебаний пластины, справедливое при любых краевых условиях. Формула Рэлея, позволяющая найти частоту свободных колебании основного тона нагруженной пластины имеет вид
определяется в результате сопоставления выражений для кинетической и потенциальной энергий колебаний системы. Метод позволяет учесть нагружение платы функционального узла установленными на ней компонентами и получить соотношение для расчета частоты свободных колебаний пластины, справедливое при любых краевых условиях. Формула Рэлея, позволяющая найти частоту свободных колебании основного тона нагруженной пластины имеет вид
 , (5.7)
, (5.7)
где  - коэффициент, характеризующий зависимость частоты свободных колебаний пластины от краевых условий; а - большая сторона пластины;
- коэффициент, характеризующий зависимость частоты свободных колебаний пластины от краевых условий; а - большая сторона пластины;  - приведенные к площади пластины массы компонентов и самой пластины.
- приведенные к площади пластины массы компонентов и самой пластины.
Коэффициент  вычисляется через отношение сторон пластины C= a /b. Формулы для расчета
вычисляется через отношение сторон пластины C= a /b. Формулы для расчета  приведены в табл. 5.1. На схемах закрепления пунктирной линией обозначено свободное опирание стороны пластины, штриховкой - жесткое закрепление.
приведены в табл. 5.1. На схемах закрепления пунктирной линией обозначено свободное опирание стороны пластины, штриховкой - жесткое закрепление.
Выражение (5.7) обеспечивает удовлетворительную точность лишь при расчете частоты свободных колебаний основного тона. С ростом номера тона точность результатов расчета существенно снижается.
С помощью метода Ритца, являющегося развитием метода Рэлея, получены формулы расчета частот свободных колебаний пластины на основном тоне и обертонах для различных краевых условий. Широкое применение находит формула
 , (5.8)
, (5.8)
где  - коэффициент, зависящий от способа закрепления пластины, соотношения ее сторон и номера тона колебаний; т - масса пластины, приведенная к площади;
- коэффициент, зависящий от способа закрепления пластины, соотношения ее сторон и номера тона колебаний; т - масса пластины, приведенная к площади;  - коэффициент, учитывающий нагрузку пластины размещенными на ней компонентами.
- коэффициент, учитывающий нагрузку пластины размещенными на ней компонентами.
Значение  находят в результате решения дифференциального уравнения колебания прямоугольной пластины при заданных краевых условиях. Для определенных комбинаций краевых условий и отношений сторон пластины
находят в результате решения дифференциального уравнения колебания прямоугольной пластины при заданных краевых условиях. Для определенных комбинаций краевых условий и отношений сторон пластины  табулирован.
табулирован.
Для упрощения процедуры расчета круговой частоты свободных колебаний пластины основного тона формула (5.8) преобразуется:
 (Гц), (5.9)
(Гц), (5.9)
где  - частотная постоянная; а - большая сторона пластины, мм;
- частотная постоянная; а - большая сторона пластины, мм;  - поправочный коэффициент на материал пластины;
- поправочный коэффициент на материал пластины; 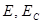 - модули упругости материала пластины и стали;
- модули упругости материала пластины и стали;  - их плотности;
- их плотности;  – поправочный коэффициент на нагружение пластины равномерно размещенными на ней элементами;
– поправочный коэффициент на нагружение пластины равномерно размещенными на ней элементами;  - масса элемента;
- масса элемента;  – масса пластины.
– масса пластины.
Значения частотной постоянной С для некоторых схем закрепления пластины приведены в табл.5.2.
Построение расчетных моделей функциональных узлов производится на основе анализа реальных конструкций и выявления характерных особенностей, оказывающих существенное влияние на динамические процессы при вибрации. Примеры моделирования некоторых конструкций функциональных узлов приведены на рис. 5.3, 5.4 и 5.5.
Узел, выполненный на печатной плате, закрепляемой в четырех точках по углам (рис. 5.3,а), представляется расчетной моделью пластины, равномерно нагруженной радиокомпонентами, со свободным опиранием со всех сторон (рис. 5.3,б). Принятый способ закрепления обосновывается тем, что при изгибных колебаниях основного тона на каждой стороне пластины укладывается полуволна, узлы перемещения совпадают с точками крепления платы. Поэтому наличие точек закрепления не сказывается на параметрах колебаний.
Расчетной моделью узла на печатной плате с размерами сторон a и b, закрепленной в шести точках по контуру (рис. 5.4,а), служит прямоугольная пластина с размерами сторон а/2 и b, свободно опирающаяся по контуру, с равномерно распределенной нагрузкой (рис. 5.4,б). Основной тон свободных колебаний определяется полуволной, укладывающейся вдоль сторон а/2 и b пластины.
Конструкция функционального узла разъемного типа (рис. 5.5,а) может быть представлена расчетной моделью в виде нагруженной прямоугольной пластины 1 с жестким закреплением двух сторон, на которых установлены контрольная колодка 3 (или планка для удобства установки узла в блоке и извлечения его) и электрический соединитель (разъем) 2, и свободным опиранием двух других сторон (рис. 5.5,б). Принятая схема закрепления обосновывается тем, что элементы 2 и 3 конструкции по сравнению с печатной платой имеют значительно большую жесткость на изгиб, а зазор между внутренними поверхностями направляющих (с помощью которых плата устанавливается в блоке) и краями платы сравним с толщиной печатной платы.
Каркасные конструкции функциональных узлов (печатная плата закреплена в рамке по контуру) в первом приближении можно моделировать пластиной с жестким закреплением всех сторон. Построение более точных расчетных моделей таких конструкций заключается в следующем.
Частота свободных колебаний основного тона конструкций печатных плат, усиленных ребрами жесткости, рамками, обечайками и другими элементами жесткости, может быть найдена по формуле Рэлея (5.7).
Применение формулы (5.7) предполагает переход от сложной конструкции узла к модели эквивалентной прямоугольной пластина с параметрами а, D и  .
.
Жесткость эквивалентной пластины на изгиб находится как  , где
, где  - цилиндрическая жесткость платы и рамки на изгиб соответственно.
- цилиндрическая жесткость платы и рамки на изгиб соответственно.
Расчет цилиндрической жесткости производится по формуле
 , (5.10)
, (5.10)
где E - модуль упругости материала платы; J - момент инерции сечения платы в плоскости изгиба; b - ширина сечения;  - коэффициент Пуассона для материала платы.
- коэффициент Пуассона для материала платы.
Таблица 5.1 Определение коэффициента 
| № схемы | Схема закрепления | Формула расчета 
| |||

| 
| ||||
 2 2
| 
| ||||
 3 3
| 
| ||||
 4 4
| 
| ||||
 5 5
| 
| ||||
 6 6
| 
|
Таблица 5.2
Значения частотной постоянной
| № схемы закрепления пластины по табл.5.1 | Значения частотной постоянной | ||||||||
|

|

|
|

|
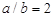
|

|

|

| |
| 23,1 | 23,8 | 28,6 | 45,8 | 74,4 | 114.5 | 166,0 | 228,9 | 389,3 | |
| 52,0 | 52,4 | 55.3 | 67,3 | 90,9 | 127,6 | 176,9 | 238,8 | 396,7 | |
| 52,1 | 52,5 | 56,2 | 74,1 | 102,5 | 170,6 | 248,5 | 345,1 | 592,8 | |
| 52,1 | 52,6 | 57,2 | 83,8 | 141,4 | 228,6 | 343,7 | 485,4 | 847,6 | |
| 23,2 | 23,9 | 32,1 | 67,6, | 131,1 | 221,4 | 337,9 | 480,9 | 843.6 | |
| 35,9 | 36,7 | 42,2 | 74,1 | 135.4 | 224,6 | 340,6 | 482,8 | 845,8 |
Значение  можно найти также с помощью (5.10), если подставить в формулу момент инерции сечения рамки. Ввиду того, что сечение рамки или других элементов жесткости узла имеет сложную конфигурацию, момент инерции сечения определяется как сумма осевых и центробежных моментов элементарных сечений правильной геометрической формы, на которые разбивается исходное сечение:
можно найти также с помощью (5.10), если подставить в формулу момент инерции сечения рамки. Ввиду того, что сечение рамки или других элементов жесткости узла имеет сложную конфигурацию, момент инерции сечения определяется как сумма осевых и центробежных моментов элементарных сечений правильной геометрической формы, на которые разбивается исходное сечение:
 ,
,
где  - осевой и центробежный моменты i-го элементарного сечения соответственно;
- осевой и центробежный моменты i-го элементарного сечения соответственно;  - площадь этого сечения;
- площадь этого сечения;  - расстояния в плоскости изгиба сечения между центрами тяжести I -го элементарного сечения и сечения рамки. Определение момента инерции сечения рамки иллюстрируется с помощью рис.5.6. Соотношения для расчета осевых моментов инерции сечений простейших геометрических форм и координат центра тяжести приведены в табл.5.3.
- расстояния в плоскости изгиба сечения между центрами тяжести I -го элементарного сечения и сечения рамки. Определение момента инерции сечения рамки иллюстрируется с помощью рис.5.6. Соотношения для расчета осевых моментов инерции сечений простейших геометрических форм и координат центра тяжести приведены в табл.5.3.
При выборе сечения рамки необходимо исходить из принципа наихудшего случая: жесткость конструкции на изгиб в сечении должна быть минимальной, что позволит найти самую низкую частоту свободных колебаний конструкции узла.
Коэффициент  , входящий в формулу (5.10), в случае закрепления пластины в четырех или шести точках по периметру, может быть найден по формуле:
, входящий в формулу (5.10), в случае закрепления пластины в четырех или шести точках по периметру, может быть найден по формуле:
 ,
,
где а, b - длина и ширина пластины.
Пример расчета частоты свободных колебаний монтажной платы приведен в Прил. 7.
Таблица 5.3 К расчету осевых моментов инерции рамки
 Форма сечения Форма сечения
| Расчетное соотношение | |||
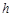
| 
 При
При  
| |||

| 

|
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...


