Расчет ударопрочности конструкций приборной аппаратуры

Конструкции АПА отвечают требованиям ударопрочности, если перемещение и ускорение при ударе не превышают допустимых значений, а элементы конструкции обладают запасом прочности на изгиб. В связи с тем, что изгибные напряжения в элементах конструкции в конечном счете определяются величиной перемещений (прогибов), расчет ударопрочности конструкции может быть сведен к нахождению запаса прочности элементов при прогибе [7,21,55].

Исходными данными для расчета являются: масса т и геометрические размеры элемента конструкции; характеристики материала (модуль упругости Е ; плотность r ; коэффициент Пуассона ); перегрузки при ударе и длительность удара .

Методика расчета заключается в следующем. На первом шаге, по заданным параметрам удара необходимо определить амплитуду ускорения при ударе , значение скорости в начальный момент удара или эквивалентную высоту падения массы .

Далее находится частота свободных колебаний конструкции , по значению которой вычисляется максимальный прогиб упругого элемента при ударе. В зависимости от модели, к которой приводится реальная конструкция, расчет частоты свободных колебаний производится по формулам (5.7) - (5.9).

Составляющим максимального прогиба упругого элемента конструкции при ударе является статический прогиб . Воспользуемся основной формулой для расчета частоты свободных колебаний, полученной из выражений (5.7)-(5.9):

,

отсюда .

Знание статического прогиба , скорости в начальный момент удара и частоты свободных колебаний позволяет найти максимальный прогиб упругого элемента (максимальное перемещение массы)

и полную динамическую деформацию Z_Д упругого элемента

.

Полная динамическая деформация определяет эквивалентную силу удара, приложенную к упругому элементу в точке удара. Допустимое напряжение в элементах конструкции при изгибе , где - предельное напряжение в материале; - коэффициент, характеризующий запас прочности: - коэффициент достоверности определения расчетных нагрузок и напряжений; - коэффициент, характеризующий степень ответственности детали; - коэффициент, учитывающий однородность механических свойств материалов.

Изгибное напряжение, возникающее в элементах конструкции при ударе, можно найти через изгибающий момент и момент сопротивления изгибу по формуле . При расчете изгибающего момента исходят из того, что сила приложена в геометрическом центре упругого элемента. Тогда реакция опор упругого элемента составит , а изгибающий момент , где - геометрический размер элемента конструкции в плоскости изгиба.

Момент сопротивления упругого элемента изгибу , где J - момент инерции сечения элемента относительно оси изгиба ; - значение координаты от нейтральной оси сечения до поверхности упругого элемента; h - толщина упругого элемента.

Пример расчета ударопрочности конструкции приведен в Прил. 7.

Основы расчета виброизоляции конструкций бортовой

Приборной аппаратуры

Одной из наиболее эффективных мер борьбы с вибрациями является виброзащита ПА с помощью различных систем виброизоляции. Между защищаемым объектом и вибрирующей поверхностью помещаются устройства - виброизоляторы, которые ослабляют вибрационные воздействия на объект.

Основным элементом виброзащитной системы служит амортизатор (виброизолятор). Амортизатор представляет собой конструкцию, объединяющую упругий и демпфирующий элементы. Упругие силы в амортизаторе создаются стальными пружинами, упругой составляющей жесткости резиновых или полимерных элементов, упругостью металлорезины или троса. Силы сопротивления (демпфирование) в конструкции амортизатора образуются в результате сухого трения в материале упругого и демпфирующего элементов и вязкого трения.

В зависимости от типа упругого элемента и способа демпфирования амортизаторы делятся на следующие квалификационные группы [7,43]:

- резинометаллические;

- пружинные с воздушным демпфированием;

- пружинные с фрикционным демпфированием;

- цельнометаллические со структурным демпфированием.

Конструкции некоторых типов амортизаторов приведены на рис. 5.7.

Виброизолирующие свойства амортизаторов определяются их параметрами, основными из которых являются:

- номинальная нагрузка амортизатора , при которой статическая деформация упругого элемента находится в пределах рекомендуемых значений;

- частота свободных колебаний при номинальной нагрузке вдоль основной оси ;

- статический прогиб при номинальной нагрузке ;

- жесткость амортизаторов k;

- параметры, характеризующие работоспособность амортизаторов в условиях климатических воздействий.

При выборе амортизаторов для системы виброизоляции принимается, что амортизаторы должны работать при номинальной нагрузке. Снижение нагрузки на амортизатор ведет к повышению жесткости, перегрузка - к снижению надежности системы.

По частотным свойствам амортизаторы подразделяются на низкочастотные (f₀=3…4 Гц), среднечастотные ( f₀ =8…10 Гц) и высокочастотные ( f₀ =20...25 Гц ).

Статический прогиб, номинальная нагрузка и жесткость амортизатора связаны соотношением .

Расчет виброизоляции состоит из четырех последовательных этапов: выбор типа амортизаторов; расстановка амортизаторов; статический расчет вибрационной системы виброизоляции; расчет динамических характеристик и эффективности амортизации. Рассмотрим методики решения этих задач.

Выбор типа амортизаторов производится по расчетному значению нагрузки и при этом учитываются масса и габаритные размеры блока, параметры внешних механических воздействий (диапазон частот вибраций, амплитуды перемещений и ускорений при вибрациях, направление действия возбуждающих колебаний), параметры климатических воздействий, параметры амортизаторов.

Расчетное значение нагрузки определяется из условия равенства общей статической грузоподъемности амортизаторов массе блока: , где m - масса блока; - число амортизаторов в системе виброизоляции. По конструктивным соображениям обычно принимают . Значение Р_А - должно быть близким к номинальной нагрузке амортизатора .

Номинальной нагрузке конкретного типа амортизаторов соответствуют параметры: статический прогиб , жесткость по основным направлениям, масса.

Расстановка (монтаж) амортизаторов. Наибольшее применение находит рациональный монтаж амортизаторов. Условия рационального монтажа заключаются в следующем: общая статическая грузоподъемность всех амортизаторов равняется массе блока; центр масс (ЦМ) и центр жесткости (ЦЖ) (т.е. точка приложения равнодействующей сил реакции амортизаторов) совпадают или лежат на одной вертикали, это обусловлено тем, что если на изолируемую систему действуют периодические возбуждающие силы с широким спектром частот, то для обеспечения высокой эффективности виброизоляции все шесть частот свободных колебаний системы должны лежать в узком диапазоне частот. Совмещение частот свободных колебаний может быть достигнуто соответствующим выбором жесткости амортизаторов и координат их расстановки [43].

Широко применяется расположение амортизаторов, при котором ЦЖ находится ниже ЦМ (рис. 5.8,а). Основным достоинством такой системы является то, что она дает возможность разместить блоки аппаратуры в непосредственной близости друг от друга. Если все амортизаторы имеют одинаковую жесткость , то смещение блока вдоль оси Z будет происходить без перекосов, т.е. исключаются повороты относительно осей Х и Y. Частота свободных колебаний вдоль оси Z для этого случая определяется соотношением

,

где - число амортизаторов; m - масса виброизолируемого объекта.

При использовании в системе (см. рис. 5.8,а) осесимметричных амортизаторов ( ) образуются две плоскости симметрии XOZи YOZ и возникают дополнительно пять связанных (сложных) колебаний блока. Перемещение точек расположения амортизаторов на боковую поверхность блока (рис. 5.8,б)

позволяет совместить ЦЖ и ЦМ и избежать связанных колебаний. Такой же результат достигается при зеркально симметричном расположении амортизаторов на нижней и верхней стенках блока (рис. 5.8,в). Для конструктивной реализации таких систем требуются дополнительные узлы крепления в виде кронштейнов и стоек. Более простой системой, позволяющей совместить ЦЖ с ЦМ, является система с наклонным расположением амортизаторов (рис. 5.8,г). Она находит применение в конструкциях с высоким уровнем вибрационных нагрузок (бортовая аппаратура, корабельная, транспортная). Комбинированные системы (рис.5.8, д) позволяют ослабить колебания вокруг горизонтальных осей за счет установки дополнительных виброизоляторов на базовой поверхности блоков.

Такая система применяется для конструкций ПА, имеющих значительную высоту. Если амортизаторы устанавливаются несимметрично относительно ЦМ блока (рис. 5.8,е), то для сохранения значений частот свободных колебаний таких же, как и при симметричном размещении, необходимо, чтобы жесткость каждого амортизатора вдоль оси Z была пропорциональна его доле нагрузки, т.е. .

При произвольном размещении амортизаторов под изолируемым объектом, когда плоскости симметрии отсутствуют, все колебания будут связаны между собой. Наличие хотя бы одной плоскости симметрии вызывает распад связанных колебаний на две не связанные между собой группы, одна из которых характеризует движение ЦМ в плоскости симметрии, другая - в перпендикулярном этой плоскости направлении.

Координаты ЦЖ амортизаторов можно вычислить через статические моменты жесткости относительно координатных плоскостей:

где - координаты расположения амортизаторов; - жесткости амортизаторов по направлениям осей координат.

Аналитически условия рациональной расстановки амортизаторов представляются в виде:

, (5.11)

где Р_i - реакция i -го амортизатора.

Первое уравнение системы (5.11) показывает, что общая грузоподъемность всех амортизаторов равна весу амортизируемого объекта, три следующие уравнения выражают условия равновесия пространственной системы параллельных сил, три последние уравнения - условия равенства нулю центробежных моментов реакций амортизаторов относительно главных центральных осей инерции блока. Равенство нулю моментов и центробежных моментов реакций амортизаторов означает совпадение ЦМ блока с ЦЖ системы виброизоляции.

Статический расчет системы амортизации представляет собой решение уравнений (5.11). При использовании в системе амортизаторов число неизвестных в уравнениях (5.11) составляет 4 . Поэтому в исходном виде система виброизоляции является статически неопределимой. Чтобы произвести расчет такой системы необходимо задать (4 -7 ) величин. Например, при = 3 требуется взять пять величин, при =4 - девять и т.д. Обычно дополнительные условия задают в виде координат расположения определенного числа амортизаторов, симметричного расположения амортизаторов относительно центра масс и др.

В результате решения уравнений (5.11) получают значения координат всех амортизаторов и их реакций P_i. Зная реакции амортизаторов, можно определить статические прогибы . Если статические прогибы амортизаторов различны, то производится выравнивание объекта с помощью компенсирующих прокладок. Толщину прокладок находят как разность статических прогибов.

Определение динамических характеристик системы и эффективности амортизации. Для выбранного типа амортизаторов и их значений жесткости находят частоту свободных колебаний блока и частотную расстройку , где -нижнее значение частоты диапазона частот внешних вибрационных воздействий. Далее проверяется условие и определяется коэффициент передачи вибраций как отношение амплитуд вынужденных колебаний Z_B и виброперемещения основания Z_A

,

где - коэффициент затухания, а 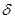- коэффициент демпфирования ( ).

Зависимость от коэффициента частотной расстройки приведена на рис. 5.9. Как видно из графика, становится меньше единицы, если значение превышает .

Эффективность виброизоляции определяется выражением Э=(1- )100%. Если значение эффективности ниже требуемой величины, то пересматривается структура системы виброизоляции. Пример расчета виброизоляции приведен в Прил. 8.