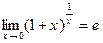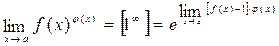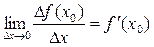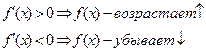Тема 8. Функция нескольких переменных

1. Основные понятия.

2. Предел и непрерывность.

3. Частные производные.

4. Дифференциал функции.

5. Производная по направлению, градиент.

6. Экстремум функции нескольких переменных.

7. Наибольшее и наименьшее значения функции.

8. Функции нескольких переменных в экономической теории.

Тема 1. Функции одной переменной. Предел функции

Ø Литература.

Забейворота В.И., Иванова В.Н., Завьялов О.Г.

Математика в экономике. Основы математического анализа. Учебное пособие. УрСЭИ, Челябинск, 2002.

При решении задач на вычисление пределов необходимо знать, что если существуют пределы функций при х®х₀

,

то можно использовать основные правила вычисления пределов.

· .

· .

·

· .

· , ,

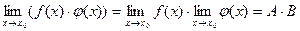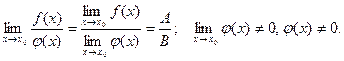
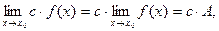
а также следующие пределы

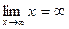1. . 2. . 3. .

4

5. Первый замечательный предел:

Следствия из первого замечательного предела:

; ; ; .

	,

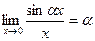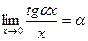6. Второй замечательный предел:

е » 2,7182… или е » 2,7

7. Если .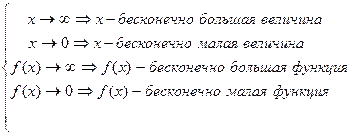

8. Если существует , то существуют и односторонние пределы:

левый и правый , причем

9. Если функция y = f(x) непрерывна в точке х₀ , то

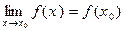или ,

в противном случае точка х₀ – точка разрыва функции.

Решение типовых примеров.

Найти указанные пределы.

1.

Функция определена и непрерывна в точке х = 2, поэтому данный предел равен значению функции в этой точке.

.

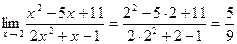2.

При подстановке в выражение под знаком предела вместо х его предельного значения х = 3 получаем неопределенность вида .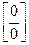

.

Функция не определена в точке х = 3, т.е. х = 3 – точка разрыва функции, но т.к. переменная х стремится к точке 3, х®3, а не равна 3, то под знаком предела можно производить тождественные преобразования выражения, не принимая во внимание его поведения в предельной точке.

Разложим квадратные трехчлены, входящие в числитель и знаменатель, на линейные множители по формуле:

ах² + bх + с = а (х-х₁)(х-х₂), где х₁ и х₂ – корни квадратного уравнения

ах² + bх + с = 0.

Найдем корни, решив уравнеие 2х² - 3х – 9 = 0;

D = b²-4ас = 9-4×2×(-9) = 81;

.

.

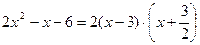Аналогично: х² – х – 6 = 0 Þ х₁ = 3, х₂ = -2, Þ х² – х – 6 = (х-3)×(х+2).

Преобразуем данный предел:

.

Функция в точке х = 3 не существует, а предел от этой функции при х ® 3 существует и равен .

3.

При подстановке предельного значения х ® ¥ получаем неопределенность вида 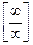, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной, или делением числителя и знаменателя на старшую степень переменной:

т.к. 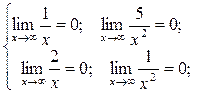как пределы от бесконечно малых величин,

как пределы от постоянных величин.

4. .

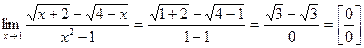Для раскрытия неопределенности 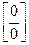умножим числитель и знаменатель на выражение, сопряженное числителю, ( ).

.

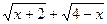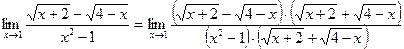Заменим в числителе произведение по формуле “разность квадратов”:

(а-b)×(а+b) = а² - b²;

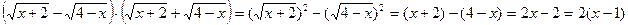В знаменателе: х² – 1 = (х-1) (х+1);

5. .

Для раскрытия неопределенности вида 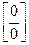в данном примере воспользуемся первым замечательным пределом и одним из его следствий:

,

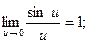
заменим предел произведения функций произведением пределов этих функций и вынесем постоянный множитель:

По первому замечательному пределу (u = 2x или u = 4x):

.

6. . Имеем неопределенность вида [1^¥]:

= [1^¥], т.к. .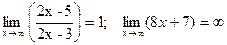

Имеем

Тогда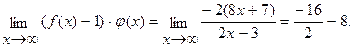

Следовательно, .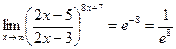

Тема 2. Производная и дифференциал функции

Ø Литература.

Забейворота В.И., Иванова В.Н., Завьялов О.Г.

Математика в экономике. Основы математического анализа. Учебное пособие. УрСЭИ, Челябинск, 2002.

Важнейшим понятием математического анализа является понятие производной функции, которая определяет скорость изменения функции относительно своего аргумента.

Производной функции y = f(х) в точке х₀ называется предел отношения приращения функции Df(x₀) = f(x₀+Dx) – f(x₀) к приращению аргумента Dx при стремлении последнего к нулю и обозначается , т.е.

Другие обозначения:

,

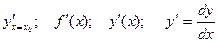где dy – дифференциал функции, dх– дифференциал аргумента.

При вычислении производных используют таблицу производных и правила дифференцирования.

Правила дифференцирования

Пусть u = u(x) и v = v(х) – непрерывные функции в точке х = х₀, тогда существуют производные от суммы, разности, произведения частного этих функций в заданной х₀.

· (u ± v)¢ = u¢ ± v¢

· (u × v)¢ = u¢ ×v + u × v¢

· (c × v)¢ = c × v¢

·

·

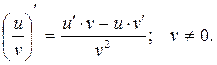
Производная сложной функции

Пусть у = f(u), а u = j(х), тогда у = f(j(х)) – сложная функция, ее производная находится по правилу дифференцирования сложной функции. Если каждая из функций у = f(u) и u = j(х) дифференцируема по своему аргументу, то

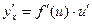или

· Следует помнить, что производная постоянной равна нулю С^¢ = 0, а

производная переменной величины х равна единице, х^¢ = 1

Таблица производных основных элементарных функций и производных сложных функций

y = f(х)	y¢ = f¢(x)	y = f(u), u = j(х)	у¢ = f¢(u)×u¢
y = xa	(xa)¢ = a×xa-1	y = ua	y¢ = a×ua-1×u¢
		y =
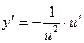
y = ax	(ax )¢ = ax×lna	y = au	y¢ = au×lna×u¢
y = ex	(ex)¢ = ex	y = eu	y¢ = eu×u¢
y = logax	(logax)¢	y=logau
y = lnx		y = lnu
y = sinx	(sinx)¢ = cosx	y = sinu	y¢ = cosu×u¢
y = cosx	(cosx)¢ = -sinx	y = cosu	y¢ = -sinu×u¢
y = tgx		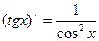y = tgu
y = ctgx		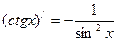y = ctgu
y = arcsinx		y = arcsinu
y = arccosx		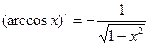y = arccosu
y = arctgx		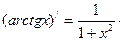y = arctgu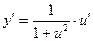
y = arcctgx		y = arcctgu

Решение типовых примеров

Найти производные данных функций.

1. ; y^'=?

По правилу дифференцирования сложной функции имеем

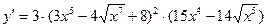
Использовано правило дифференцирования алгебраической суммы:

2.

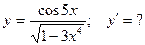
Применим правило дифференцирования частного:

=

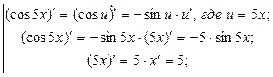
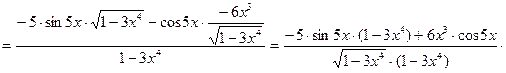
Итак,

3.

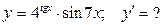
Применим правило дифференцирования произведения.

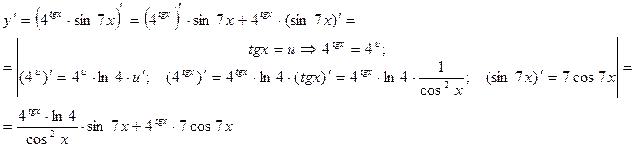
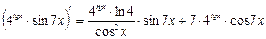
4. у = ln(arcsin8x); y¢ =?

Имеем y=lnu; где u=arcsin8x. Тогда

Дифференциал функции – понятие столь же часто используемое в математике как и производная.

Дифференциал функции у = f(х) в точке х₀ вычисляется по формуле

df(x) = f ¢(x₀)·dx или dy = y ¢·dx,

где dx – дифференциал аргумента, а у^¢ - производная функции, поэтому вычисление дифференциала функции сводится к технике нахождения ее производной.

5. Найти дифференциал функции у = arctg2х.

Тема 3. Исследование функции и построение графиков

Ø Литература

Забейворота В.И., Иванова В.Н., Завьялов О.Г.

Математика в экономике. Основы математического анализа. Учебное пособие. УрСЭИ, Челябинск, 2002.

Полное исследование функции y=f(x) и построение ее графика рекомендуется проводить по следующей схеме:

1. Найти область определения функции – множество значений аргумента, при которых функция имеет смысл D(x) = {x: y=f(x)}.

f(-x) = f(x) Þ функция четная: график симметричен относительно оси 0у.

f(-x) = -f(x) Þ функция нечетная: график симметричен относительноначала координат O(0;0).

функция общего вида (нет симметрии).

3. Установить характер точек разрыва функции (если они имеются) и исследовать поведение функции в бесконечности.

4. Найти асимптоты графика функции:

а). Bертикальные.

Вертикальные асимптоты проходят через точки бесконечного разрыва функции.. Если т. х₀ – точка бесконечного разрыва функции, т.е.

,

то х = х₀ – уравнение вертикальной асимптоты.

б). Наклонные.

Уравнение этих асимптот находят в виде y = kx + b.

Для правой ветви графика функции

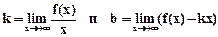
Для левой ветви графика функции

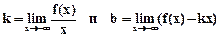
Если k = 0, то y = b - уравнение горизонтальной асимптоты.

5. Найти экстремумы функции (max или min) и интервалы монотонности функции (возрастания, убывания).

Если на (а, b)

 

Если в окрестности критической точки 1 рода х₀ (эти точки ищут из условия y' = 0) первая производная функции меняет знак

с “-”на“+”Þ вх₀ – min, f(x₀) = f_min

с “+”на“-”Þ вх₀ – max, f(x₀) = f_max

6. Найти интервалы выпуклости и вогнутости функции и точки перегиба.

Если на интервале (а, b)

Если в окрестности критической точки 2 рода х₀ (эти точки ищут из условия :y ^"= 0) вторая производная функции меняет знак, то эта точка – точка перегиба:

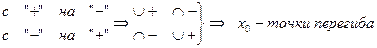
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график:

с осью Оy: x =0 Þ y = f(0),

с осью Ох: y = 0 Þ f(x) = 0 – это уравнение решают только в случае, если онопростое.

8. По результатам исследования по пунктам 1-7 построить график данной функции.

 

Решение типовых примеров

 

Исследовать функцию и построить ее график.

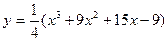
1) Найдем область определения данной функции.

D(x)– множество всех действительных значений аргумента х- вся числовая ось:

2) Исследуем данную функцию на четность, нечетность и периодичность.

.

Имеем f(-x )≠ f(x), т.е. данная функция не является четной.

Кроме того, f(-x) ≠ -f(x), т.е. данная функция не является нечетной.

Таким образом, наша функция является функцией общего вида (нет симметрий). Функция не является периодической.

3) Исследуем характер точек разрыва функции и поведение функции в бесконечности.

Так как функция определена на всей числовой оси, то она всюду непрерывна и нет точек разрыва функции. Имеем

 

 

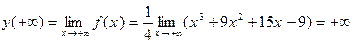
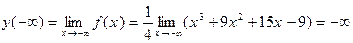
4) Найдем асимптоты графика функции.

Вертикальные.

Так как нет точек бесконечного разрыва функции, то нет вертикальных асимптот.

Наклонные асимптоты находим в виде y = kx + b.

123456