
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
· Линейными неоднородными дифференциальными уравнениями второго порядка с постоянными коэффициентами. называются уравнения вида
y" + py' + qy = f(x) (1),
где
р и q – произвольные постоянные,
f(x) – некоторая непрерывная функция.
Общее решение неоднородного линейного дифференциального уравнения (1) находят в виде:
у = y0 + yчаст. ,
где
у0 - общее решение соответствующего линейного однородного уравнения:
y" + py' + qy = 0 ,
yчаст. - частное решение исходного неоднородного уравнения (1).
· Установлено, что если функция f(x) имеет вид: f(x ) = Pn(х)×еaх, где Pn(х) – многочлен n степени, a-const, aÎR, то yчаст находят в следующем виде:
1. Если число a не является корнем характеристического уравнения к2+рк+q=0, то
yчаст .= Qn(x)eax
2. Если a совпадает с одним из корней характеристического уравнения к2+рк+q=0 : a = k1 или a = k2, то
yчаст.= x×Qn(x)×eax
3. Если оба корняхарактеристического уравнения к2 + рк + q = 0 равны a: k1 = k2 = a, то
yчаст. = x2×Qn(x)×eax
· Здесь Qn(x) – многочлен степени n с неопределенными коэффициентами, которые в дальнейшем подлежат определению (см. примеры).
Решение типовых примеров
1. Найти общее решение (общий интеграл) дифференциального уравнения.
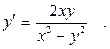
Данное уравнение не является уравнением с разделяющимися переменными вида y' = f1(x)×f2(y). Проверим, не является ли оно однородным дифференциальным уравнением первого порядка вида y' = f(x,y), где
f(lx,ly) = f(x,y):

т.е. исходное уравнение является однородным.
Введем замену:

Подставим в исходное уравнение: 
Ø Разделим переменные:
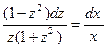
Ø Проинтегрируем полученное уравнение с разделенными переменными:

Ø Найдем интеграл левой части уравнения:
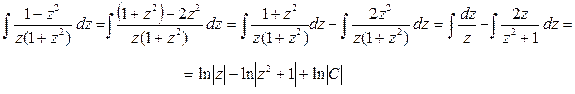
Ø Найдем интеграл правой части уравнения:
 .
.
Ø Приравняем найденные результаты:

Ø Используем свойства логарифмов:
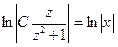 .
.
Ø Потенцируем равенство:

Ø Подставим вместо  получим
получим
 .
.
Ø Общее решение данного дифференциального уравнения имеет вид:
 ,
,
где С – произвольная постоянная.
2. Найти частное решение однородного дифференциального уравнения второго порядка при заданных начальных условиях:
 .
.
Составим для данного д. уравнения характеристическое уравнение:
k2 - 6k + 8 = 0
Оно имеет два различных, действительных корня
k1 = 2; k2 = 4.
Тогда общее решение уравнения имеет вид:
y = C1e2x + C2e4x,
где С1 и С2 – произвольные постоянные.
Найдем производную общего решения у':
y' = 2C1e2x + 4C2e4x,
Используя начальные условия получим следующую систему уравнений:

Решаем систему относительно С1 и С2 найдем: С1 = 1; С2 = 0.
Подставим найденные значения С1 и С2 в общее решение, получим искомое частное решение, удовлетворяющее заданным начальным условиям:
y = e2x
3. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

Общее решение данного уравнения находим в виде:
y = y0 + yчаст.
Ø Найдем общее решение у0 соответствующего однородного дифференциального уравнения

Ø Составим характеристическое уравнение:
k2 - k – 6 = 0 (3)
Найдем его корни: k1 = -2; k2 = 3 – действительные и различные, поэтому общее решение имеет вид:
 ,
,
где С1 и С2 – произвольные постоянные.
Ø Найдем частное решение уравнения (1).
Так как функция f(x) = (2x-1)e2x имеет вид Pn(x)eax, где Pn(x) = 2x -1 – многочлен 1-ой степени и a = 2 не является корнем характеристического уравнения, то частное решение уравнения (1) запишем в виде:
yчаст.= (Ax +B)e2x (5)
где А и В – коэффициенты, подлежащие определению. Воспользуемся методом неопределенных коэффициентов.
Найдем yч' и yч"

и подставим их в уравнение (1):
4е2х(Ах +А +В)- е2х(2Ах + А +2В)-6е2х(Ах + В) =(2х -1) е2х;
Поделим обе части уравнения на е2х :
4(Ах +А + В) - (2А + А + 2В) - 6(Ах +В) = 2х - 1 Þ
4Ах + 4А + 4В - 2Ах – А – 2В - 6Ах - 6В = 2х - 1 Þ
-4Ах+(3А-4В) = 2х-1 Þ - 4Ax = 2x ; 3A- 4B= -1.
Откуда следует, что коэффициенты А и В должны удовлетворять, следующей системе уравнений:

Решив ее, найдем А= -0,5; B= -0,125.
Ø Подставим найденные значения А и В в уравнение (5) и найдем частное решение:

Следовательно, общее решение данного линейного неоднородного дифференциального уравнения второго порядка (1) имеет вид:

Тема 7. Ряды
Ø Литература
Забейворота В.И., Иванова В.Н., Завьялов О.Г.
Математика в экономике (Основы математического анализа). Учебное пособие. УрСЭИ, Челябинск, 2002
Пусть дана бесконечная числовая последовательность
a1, a2, a3,,…,an, …= {an} (1)
которая считается заданной, если задана формула (закон), по которой вычисляется общий n-й (энный) член этой последовательности:
an = f(n), n = 1,2,3,…
· Под числовым рядом понимают бесконечную сумму членов заданной бесконечной числовой последовательности:
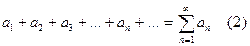
Для данного ряда можно составить последовательность его частичных сумм:
S1,S2,S3,…Sn,…= {Sn} (3),
где
S1=a1
S2= a1+ a2
S3= a1+ a2+a3
……
Sn= a1+ a2+a3+…+an - n-я частичная сумма ряда
Предположим, что закон по которому образуется Sn известен:
Sn = F(n)
· Если существует предел частичной суммы

равный некоторому числу S, т.е.  то это число называют суммой ряда и обозначают:
то это число называют суммой ряда и обозначают:

При этом говорят, что ряд сходится к данному числу S.
· Если же предел частичной суммы

не существует или равен бесконечности, то ряд суммы не имеет и говорят, что он расходится.
Пусть дан, сходящийся ряд:

Составим разность S – Sn:
S – Sn = an+1 + an+2 + an+3 +… или S – Sn = Rn,
где Rn = an+1 + an+2 + an+3 +…и называется остатком ряда.
Вычислим предел
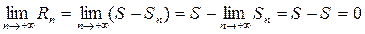
Таким образом, для сходящихся рядов выполняется равенство
S = Sn + Rn ,

Итак, можно следующим образом вычислять приближенно сумму ряда S:
Ø взяв n = 10 (10 членов ряда) найдем S » S10, где R10 и будет погрешностью вычислений;
Ø взяв n = 100 (100 членов ряда) найдем S » S100, где R100 и будет погрешностью вычислений;
Ø взяв n=1000 (1000 членов ряда) найдем S » S1000, где R1000 и будет погрешностью вычислений.
При этом каждый раз сумма ряда будет вычисляться все точнее и точнее, все с меньшей и меньшей погрешностью.
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...