Исследовать и построить график функции

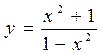
1) Найдем область определения данной функции.

. Данная функция определена и непрерывна на всей числовой оси, кроме точек х = -1 и х = 1, т.к. в этих точках функция не определена, т.е. х = -1 и х = 1 - точки разрыва функции:

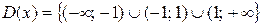
2) Исследуем данную функцию на четность, нечетность и периодичность.

.

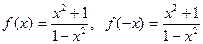Имеем f(-x) = f(x), т.е. данная функция является четной и ее график симметричен относительно оси Оy. Поэтому дальнейшие исследованиябудем проводить для х≥0.

Функция не является периодической, т.к. f(x + T) = f(x) только при Т = 0.

3) Исследуем характер точек разрыва функции и поведение функции в бесконечности.

Имеем х = 1 – точка разрыва функции.

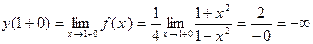
Отсюда следует, х = 1 – точка бесконечного разрыва 2 рода.

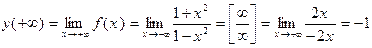
(при вычислении предела применялось правило Лопиталя):

4) Найдем асимптоты графика функции.

Вертикальные.

Так какх = 1 -точка бесконечного разрыва функции,то

х = 1 – уравнение вертикальной асимптоты.

Наклонные.

y = kx + b

Для правой ветви графика функции имеем

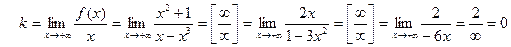
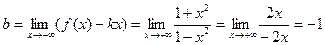
Таким образом, y = -1 – уравнение горизонтальной асимптоты для правой ветви графика..

5). Найдем интервалы монотонности и экстремум функции.

Вычислим первую производную функции:

_.

Найдем критические точки 1 рода из условий y' = 0.

y' = 0 при 4x = 0, т.е. x = 0 - критическая точка первого рода .

Отметим эту точку на числовой оси и разобьем область определения исследуемой функции ( для х³0 ) на интервалы (0; 1) и (1; +¥).

+ +

0 1 х

Найдем знак y' на каждом из интервалов:

(0; 1): y'(0,5) = 4·0,5/(1-0,5²)² = 2/(0,75)² > 0 Þ

Функция возрастает на данном интервале

(1; +¥): y'(2) = 4·2/ (1-2²)² = 8/9 > 0 Þ

Функция возрастает на данном интервале.

6) Найдем интервалы выпуклости функции и точки перегиба.

Вычислим вторую производную функции:

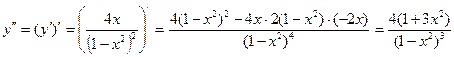
Найдем теперь критические точки 2 рода из условий y" = 0.

y" = 0 при 3x² + 1 = 0 - уравнение решений не имеет Þ

нет критических точек 2 рода.

Отметим на числовой оси область определения функции ( для х³0 )

È Ç

+ -

0 1 х

Найдем знак y^" на каждом из интервалов:

(0; 1): y' (0,5) = 4·(1+3·0,5²)/(1-0,5²)³ = 4·1,75/(0,75)³ > 0 Þ

направление выпуклости вниз È на данном интервале.

(1; +¥) : y' (2) = 4·(1+3·4)/(1-4)³ = 4·13/(-27) < 0 Þ

направление выпуклости вверх на данном интервале.

7) Найдем точки пересечения с осями координат..

С осью 0у : х=0 Þ y=1; точка пересечения – (0;1)

Таблица результатов исследования

х	0	(0;1)	(1;+¥)
y'	0	+	+
y"		+	-
y	1	Возрастает, выпукла вниз	Возрастает, выпукла вверх
	min	È	Ç

График функции

Строим график для х≥0 и отражаем его симметрично относительно оси Оy.

y

-1 0 1 x

-1

Тема 4. Неопределенный интеграл

Ø Литература

Забейворота В.И., Иванова В.Н., Завьялов О.Г.

Математика в экономике. Основы математического анализа. Учебное пособие. УрСЭИ, Челябинск, 2002.

· Интегрирование является действием обратным по отношению к дифференцированию.

· Основными понятиями этой темы являются понятия первообразной и неопределенного интеграла.

· Если в некоторой области Х определены функции f(х) и F(х), то функция F(х) называется первообразной для функции f(х), если "хÎХ выполняется равенство:

F'(x) = f(x) или dF(x) = f(x)dx

· Совокупность всех первообразных F(х)+С для функции f(x) на промежутке X и называется неопределенным интегралом от функции f(х) на этом промежутке и обозначается символом

 

 

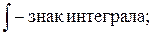
f(x) – подынтегральная функция;

f(x)dx – подынтегральное выражение;

х – переменная интегрирования;

dx – дифференциал переменной интегрирования;

F(х) – первообразная для функции f(x);

F(x)+C - множество (семейство) первообразных;

С = const - произвольная постоянная.