Радиус и интервал сходимости степенного ряда

Функциональный ряд вида:

называется рядом по степеням (x - a), где с₁,с₂, …,с_n…. - коэффициенты ряда и a – некоторое число.

Если a = 0, то имеем ряд по степеням х:

Доказано, что для степенных рядов область сходимости может меняться от одной точки до всей числовой оси, возможны 3 случая:

1) ряд сходится в одной точке x=a;

2) ряд сходится в некотором интервале (a - R; a + R), симметричном относительно точки x = a и называемом интервалом сходимости;

3) ряд сходится на всей числовой оси (-¥; +¥)

Число R, называемое радиусом сходимости степенного ряда, можно определить по следующей формуле

В граничных точках х = a ± R вопрос о сходимости ряда должен рассматриваться для каждой граничной точки в отдельности.

Область сходимости степенного ряда – это его интервал сходимости и, возможно, одна или обе его граничные точки x = a - R и x = a + R .

Решение типовых примеров.

1. Исследовать на сходимость с помощью признака Даламбера знакоположительный ряд.

Общий член ряда:

Найдем а_n+1 , заменив в формуле общего члена ряда n на (n+1)

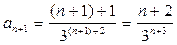
Вычислим предел:

По признаку Даламбера делаем вывод.

· Предел существует и равен ряд сходится.

 

2. Исследовать на сходимость с помощью признака Лейбница знакочередующийся ряд.

Рассмотрим абсолютные величины членов данного ряда.

Следовательно, члены данного ряда монотонно убывают по абсолютной величине.

Найдем

 

· По признаку Лейбница ряд сходится, причем

Если

то погрешность вычисления .

 

3. Найти радиус сходимости степенного ряда и исследовать его сходимость на концах интервала сходимости.

Имеем

 

 

 

 

Вычислим радиус сходимости ряда:

 

Интервал сходимости данного ряда: (-7; 7)

 

 

Исследуем сходимость ряда на концах интервала в точках х = -7 и х = 7.

 

При х = -7 ряд примет вид:

 

Исследуем на сходимость полученный знакочередующийся ряд по признаку Лейбница:

1. Каждый предыдущий член ряда больше последующего:

2.Предел общего члена ряда равен нулю:

 

Оба условия признака Лейбница выполняются и ряд сходится, т.е. точка

х = -7 принадлежит области сходимости данного степенного ряда..

При х = 7 ряд принимает вид:

.

Исследуем на сходимость знакоположительный ряд

Данный ряд расходится как гармонический ряд,.

Поэтому точка х = 7 не принадлежит области сходимости числового ряда.

 

Следовательно, область сходимости данного степенного ряда хÎ[-7; 7)

 

Тема 8. Функции многих переменных

 

Решение типовых примеров

1. Найти частные производные функции z = 3x + x²y³.

Написать уравнение линий уровня f(х; у) = с при с = 0 и с = 1.

Найти grad z в точке М₀(-1; 1).

 

· Найдем частные производные первого порядка:

Учитывая формулы и обычные правила дифференцирования функции одной переменной, находим частные производные первого порядка. При этом следует помнить, что при вычислении частной производной по х, мы считаем у постоянной. Аналогично, при нахождении частной производной по у считаем х постоянной.

 

 

· Найдем частные производные второго порядка:

 

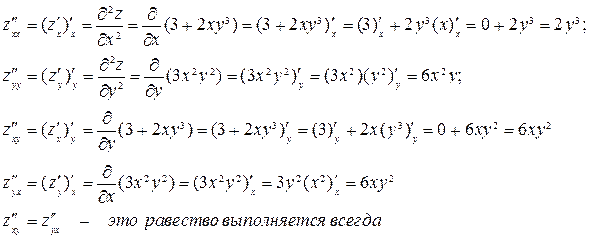
· Запишем уравнения линий уровня.

 

Как известно, линии уровня образуют на плоскости семейство параллельных кривых, на каждой из которых функция принимает постоянное значение f(x,y) = c.

При с = 0 имеем линию уровня: 3x + x²y³ = 0.

При с = 1 уравнение линии уровня: 3x + x²y³ = 1

При переходе от одной линии уровня к другой значение функции изменяется. Направление наибольшего возрастания указывает вектор

 

 

· Найдем градиент z в точке М₀(-1; 1).

Имеем

 

Итак,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачи Семестрового задания №2 (Контрольной работы №2)

 

1. Задачи №1-30

 

Вычислить пределы

1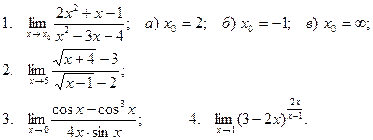
2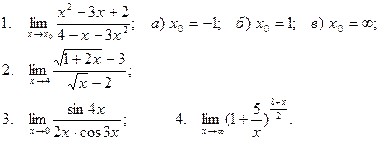
3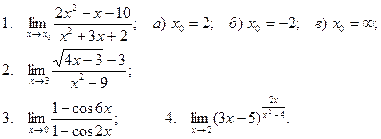
4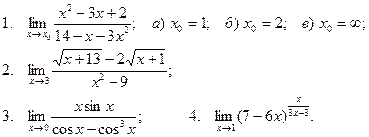
5
6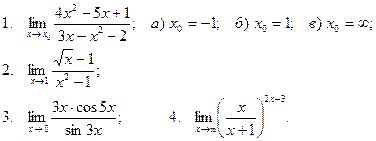
7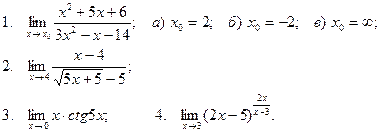
8
9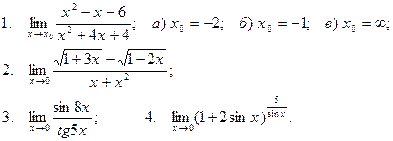
10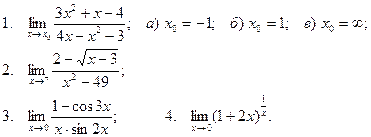
11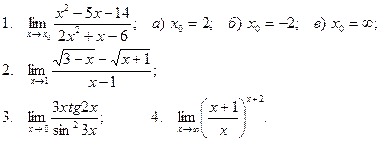
12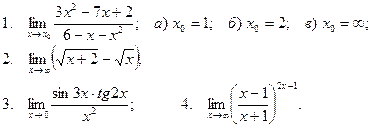
13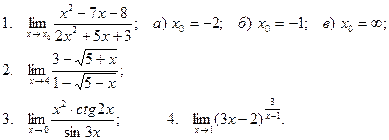
14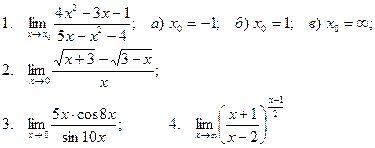
15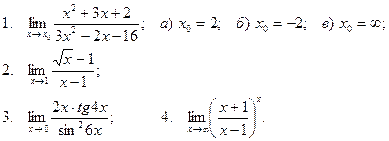
16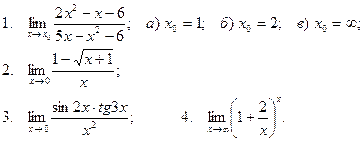
17
18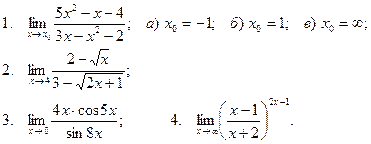
19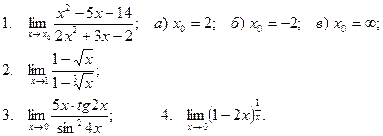
20
21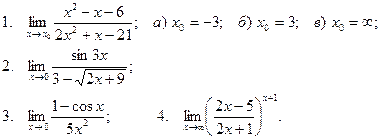
22
23
24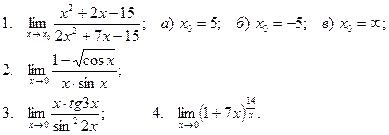
25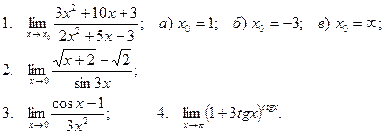
26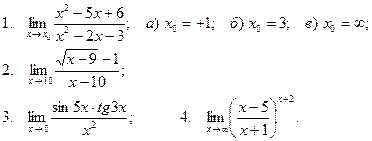
27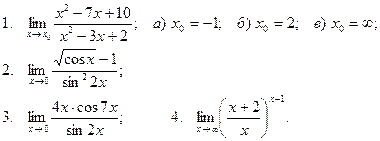
28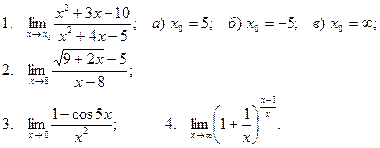
29
30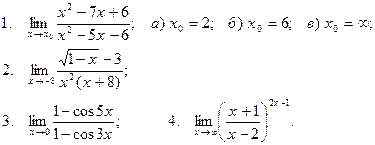

2. Задачи №31-60

Найти производные заданных функций

31
32
33
34
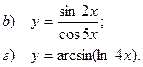
35
36
37
38
39
40
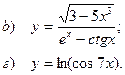
41
42
43
44
45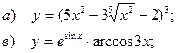
46
47
48
49
50
51
52
53
54
55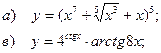
56
57
58
59
60

3. Задачи №61-90

Исследовать функцию и построить ее график

61
62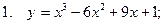
63
64
65
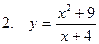
66
67
68
69
70
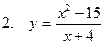
71
72
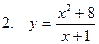
73
74
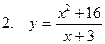
75
76
77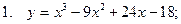
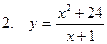
78
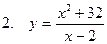
79
80
81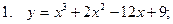
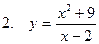
82
83
84
85
86
87
88
89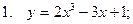
90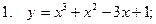

4. Задачи №91-120

Найти неопределенные интегралы

91
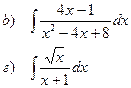
92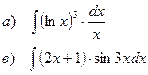
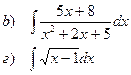
93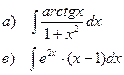
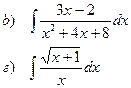
94
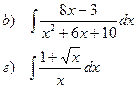
95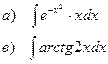
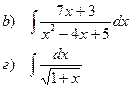
96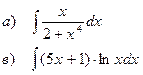
97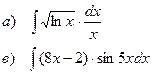
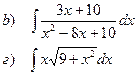
98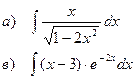
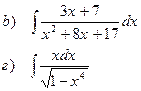
99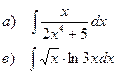
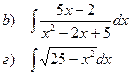
100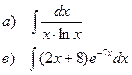
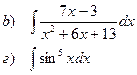
101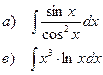
102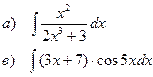
103
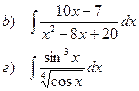
104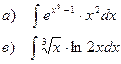
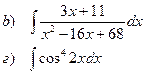
105
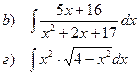
106
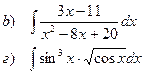
107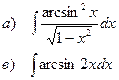
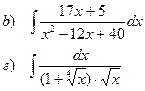
108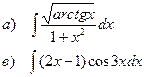
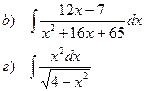
109
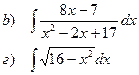
110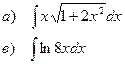
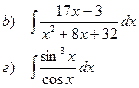
111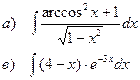
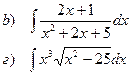
112
113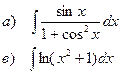
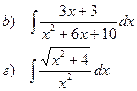
114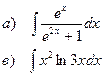
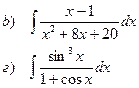
115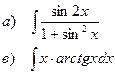
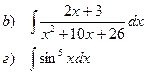
116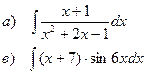
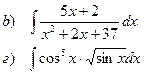
117
118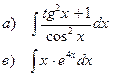
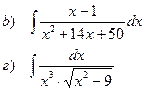
119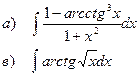
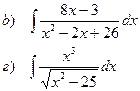
120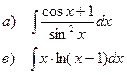

5. Задачи №121-150

а). Вычислить определенный интеграл

b). Найти площадь фигуры, ограниченной заданными линиями

в). Вычислить несобственный интеграл 2 рода

г). Вычислить несобственный интеграл 1 рода

121
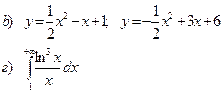
122
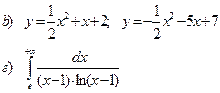
123
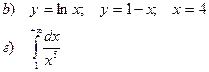
124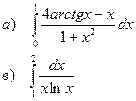
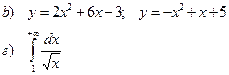
125
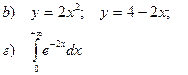
126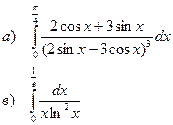
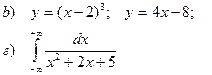
127
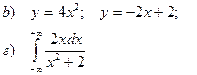
128
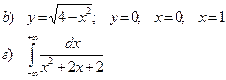
129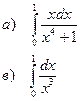
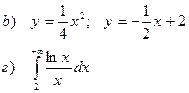
130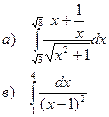
131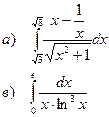
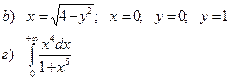
132
133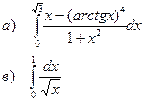
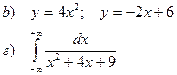
134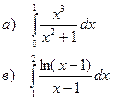
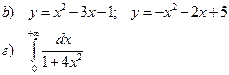
135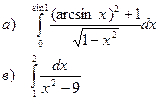
136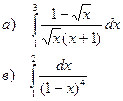
137
138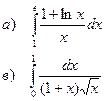
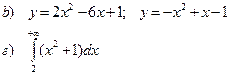
139
140
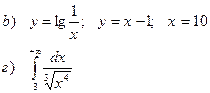
141
142
143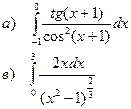
144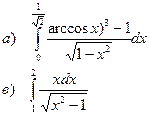
145
146
147
148
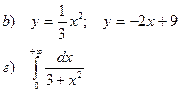
149
150

6. Задачи №151-180

Найти:

а) общее решение (общий интеграл) однородного дифференциального уравнения,

б) частное решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям.

в) общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.

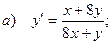
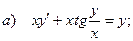
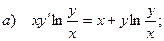
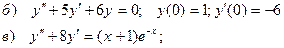
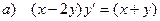
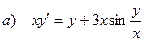
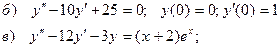
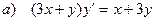
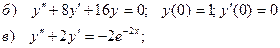
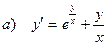
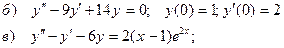
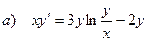
7. Задачи №181-210

Исследовать на сходимость:

а) с помощью признака Даламбера знакоположительный ряд;

б) с помощью признака Лейбница знакочередующийся ряд, вычислить приближенно S » S₄ и S » S₈ и оценить погрешность вычислений;

в) найти радиус cходимости степенного ряда и исследовать его сходимость на концах полученного интервала.

181
182
183
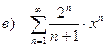
184
185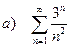
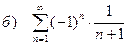
186
187
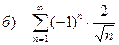
188
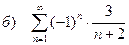
189
190
191
192
193
194
195
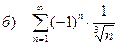
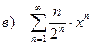
196
197
198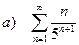
199
200
201
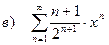
202
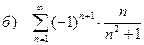
203
204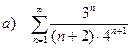
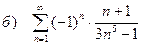
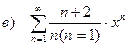
205
206
207
208
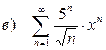
209
210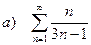

8. Задачи №211-240

1. Найти частные производные второго порядка функции z = f(х;у).

2. Написать уравнение линии уровня f(х; у) = С при С = 0 и С = 1.

3. Найти grad z в точке М₀.

211
212
213	123456
	Последнее изменение этой страницы: 2016-06-09 lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...