
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Методы получения 1-го опорного решения.
В рассмотренном нами примере (п. 1.7.) с самого начала каноническая задача линейного программирования имела симплексную форму. Рассмотрим теперь на примере, как для произвольной задачи ЛП получить первую симплекс-таблицу.
Пример №1. Найти решение задачи:
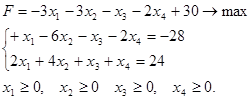 (1)
(1)
I-ый способ решения.
Запишем задачу (1) в виде таблицы, подобной симплексной.

| 
| 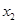
| 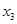
| 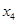
| 
| |
| - 6 | - 1 | - 2 | - 28 | |||
| (2) | ||||||
Первые две строки фактически содержат матрицу ограничений, а последняя, индексная, строка определение функции  . Конечно, таблица (2) не является симплексной. Во-первых, столбец свободных членов
. Конечно, таблица (2) не является симплексной. Во-первых, столбец свободных членов 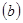 содержит отрицательный элемент (–28) в первой строке. Чтобы этого не было, умножим первую строку на (–1):
содержит отрицательный элемент (–28) в первой строке. Чтобы этого не было, умножим первую строку на (–1):

| 
| 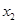
| 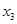
| 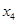
| 
| |
| - 1 | ||||||
| (3) | ||||||
Во-вторых, система ограничений не имеет разрешенного вида, то есть матрица ограничений в (3) не содержит единичной матрицы размера 
Приведем систему в таблице (3) методом Гаусса к разрешенному виду, не нарушая при этом условие неотрицательности столбца свободных членов  . Выберем, например, в качестве ведущего столбца столбец
. Выберем, например, в качестве ведущего столбца столбец  . Ведущую строку определим с помощью минимального допустимого отношения
. Ведущую строку определим с помощью минимального допустимого отношения 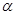 . Как обычно рамкой выделим ключевой элемент стоящий на пересечении ведущих строки и столбца.
. Как обычно рамкой выделим ключевой элемент стоящий на пересечении ведущих строки и столбца.

| 
| 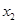
| 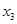
| 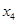
| 
| 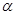
| |
| - 1 | |||||||
24 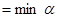
| (4) | ||||||
Методом Гаусса преобразуем ведущий столбец в базисный. Для этого:
1. из первой строки вычтем ведущую (вторую)
2. из индексной строки (третьей) вычтем ведущую вторую).
Получим новую таблицу:

| 
| 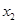
| 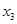
| 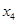
| 
| |
| - 3 | ||||||
| (5) | ||||||
| - 1 |
Теперь выберем ведущим столбец 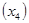 и найдем ведущую строку с минимальным допустимым отношением:
и найдем ведущую строку с минимальным допустимым отношением:

| 
| 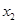
| 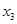
| 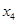
| 
| 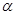
| |
| - 3 | 4 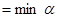
| (6) | |||||
| - 1 |
Преобразуем ведущий столбец в базисный. Для этого вычтем из второй и третьей строки ведущую (первую) строку. В результате получим таблицу:

| 
| 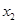
| 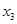
| 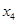
| 
| |
| - 3 | (7) | |||||
| - 3 |
которая является симплексной. Действительно, матрица системы содержит единичную (если переставить столбцы ( 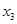 ) и (
) и ( 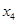 )), подматрицу размера
)), подматрицу размера  ; столбец
; столбец  неотрицателен; функция F зависит только от свободных переменных
неотрицателен; функция F зависит только от свободных переменных  и
и 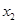 , что видно из того, что в индексной строке в столбцах базисных переменных
, что видно из того, что в индексной строке в столбцах базисных переменных 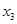 и
и 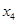 стоят нули.
стоят нули.
Далее можно решить задачу описанным выше симплекс-методом. Это решение мы запишем в виде единой таблицы, состоящей из последовательно полученных симплекс-таблиц:

| 
| 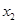
| 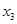
| 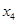
| 
| 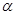
| |
| - 3 | 2 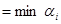
| ||||||
| - 3 | |||||||
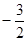
| 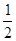
| (8) | |||||
| - 3 | |||||||
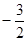
| 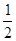
| - | |||||
| - 1 | 2 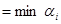
| ||||||

| 
| ||||||
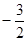
| 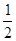
| ||||||

| 
| ||||||

| 
| ||||||
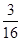
| 
| ||||||

| 
| ||||||

| 
|
Последовательность операций.
1. Выбираем ведущим второй столбец по элементу (–3) в индексной строке.
2. Находим минимальное отношение  .
.
3. Выбираем ведущей первую строку.
4. Делим ведущую строку на ключевой элемент 2 (в рамочке), стоящий в ведущей строке
5. Вычитаем из второй строки ведущую, умноженную на 2.
6. Прибавляем к индексной строке ведущую, умноженную на 3.
7. Выбираем ведущим первый столбец по элементу  в индексной строке.
в индексной строке.
8. Определяем ведущую строку с минимальным допустимым отношением  .
.
9. Делим ведущую строку на ключевой элемент 8.
10. Прибавляем к первой строке ведущую, умноженную на  .
.
11. Прибавляем к индексной строке ведущую, умноженную на 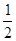 .
.
В результате всех операций 1-11 мы из первой симплекс-таблицы (7) получаем последнюю симплекс-таблицу:

| 
| 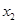
| 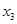
| 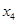
| 
| |
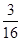
| 
| (9) | ||||

| 
| |||||

| 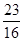
|
и из первого опорного решения
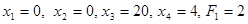 , (10)
, (10)
получаем последнее опорное решение:
 , (11)
, (11)
которое оказывается оптимальным, поскольку в индексной строке таблицы (9) нет отрицательных элементов.
Пример № 1 решен.
Ответ: 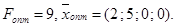
Изложенный выше метод получения первого опорного решения основан на методе Гаусса и теореме о минимальном допустимом отношении.
2-ой способ решения.
Метод искусственного базиса.
Запишем задачу (1) в виде:
 (12)
(12)
Рассмотрим вспомогательную задачу:

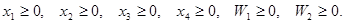
Ясно, что, если система ограничений (12) совместна, то решение задачи (13) существует и 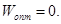 Очевидно, верно и обратное, то есть, если задача (13) имеет оптиальное решение и
Очевидно, верно и обратное, то есть, если задача (13) имеет оптиальное решение и 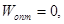 то система ограничений (12) имеет решение, причем полученное решение задачи (12) является опорным.
то система ограничений (12) имеет решение, причем полученное решение задачи (12) является опорным.
Задачу (13) нетрудно решить симплекс-методом.
Условие: 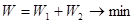 , заменим равносильным:
, заменим равносильным: 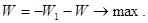
Дальнейшее решение запишем в виде таблицы.

| 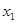
| 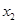
| 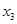
| 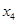
| 
| 
| 
| 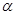
| |||||
 0 0
| - 1 | Первая таблица (не симплексная) | |||||||||||
 0 0
| - 1 | Вторая таблица (не симплексная) | |||||||||||
| - 6 | - 1 | - 2 | - 28 | ||||||||||
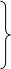 0 0
| - 1 | Третья таблица (симплексная) | |||||||||||
| - 1 | - 10 | - 2 | - 3 | - 52 | |||||||||
 0 0
| - 3 | - 1 | Далее решаем симплекс-методом | ||||||||||
| - 2 | - 1 | - 4 | |||||||||||
| - 3 | - 1 | ||||||||||||
| - 1 | |||||||||||||
| (14) | |||||||||||||
Первая таблица не является симплексной, поскольку в базисных столбцах 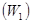 и
и  в индексной строке вместо нулей стоят единицы. Вычитая из индексной строки сначала первую строку, а затем вторую строку, получаем третью таблицу, которая оказывается уже симплексной. Далее решаем задачу как обычно, симплекс-методом. Из последней симплекс-таблицы вспомогательной задачи находим оптимальное решение этой задачи:
в индексной строке вместо нулей стоят единицы. Вычитая из индексной строки сначала первую строку, а затем вторую строку, получаем третью таблицу, которая оказывается уже симплексной. Далее решаем задачу как обычно, симплекс-методом. Из последней симплекс-таблицы вспомогательной задачи находим оптимальное решение этой задачи:

Поскольку 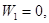 и
и 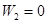 , то равенства
, то равенства  ,
, 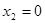 ,
, 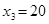 ,
, 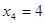 дают нам первое опорное решение исходной задачи. Этому решению соответствует таблица:
дают нам первое опорное решение исходной задачи. Этому решению соответствует таблица:

| 
| 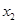
| 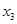
| 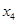
| 
| |
| - 3 | (15) | |||||
Вычитая из последней (индексной) строки 1-ую строку, умноженную на 2, и 2-ую строку, получаем таблицу (7). Далее решение совпадает с изложенным ранее.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...